现代控制理论实验 Impulse Response From in(1) 图21两输入一两输出线性定常系统 图22单输入一单输出线性定常系统
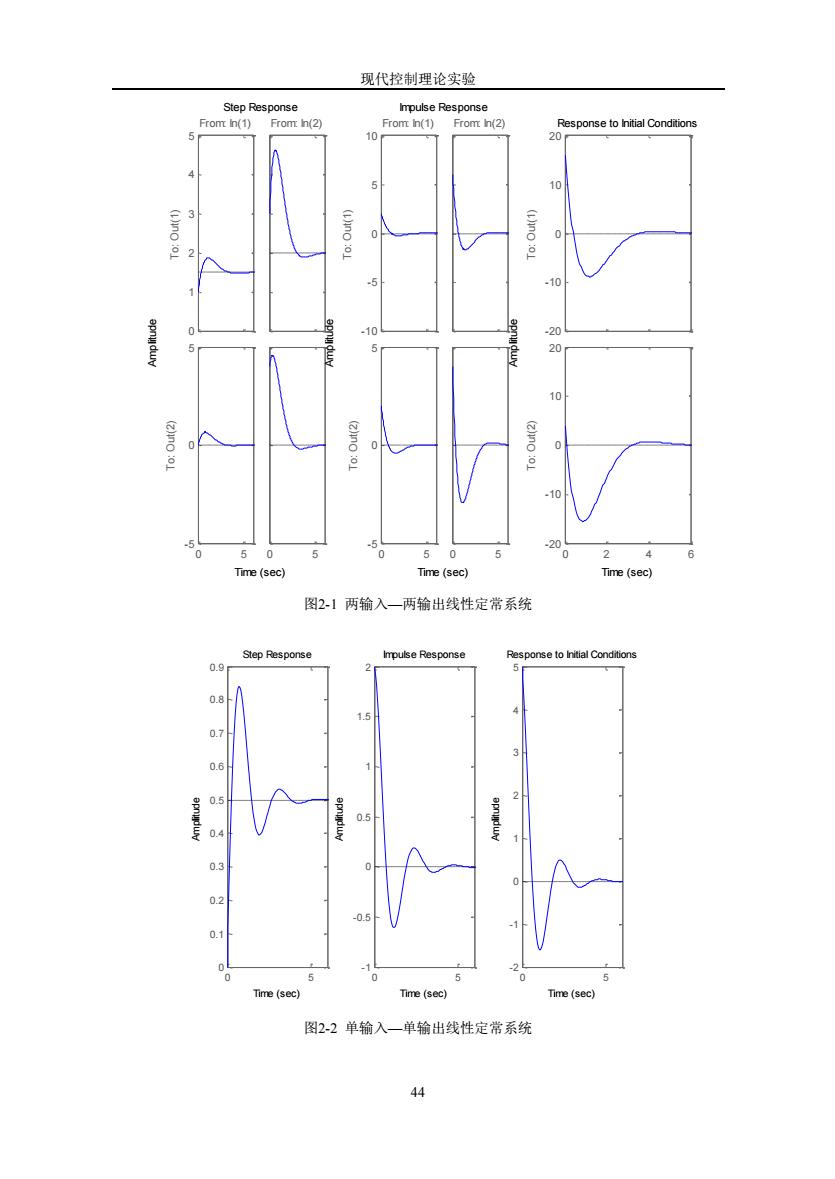
现代控制理论实验 44 0 1 2 3 4 5 To: Out(1) From: In(1) 0 5 - 5 0 5 To: Out(2) From: In(2) 0 5 -10 - 5 0 5 10 To: Out(1) From: In(1) 0 5 - 5 0 5 To: Out(2) From: In(2) 0 5 -20 -10 0 10 20 To: Out(1) 0 2 4 6 -20 -10 0 10 20 To: Out(2) Step Response Time (sec) Amplitude Impulse Response Time (sec) Amplitude Response to Initial Conditions Time (sec) Amplitude 图2-1 两输入—两输出线性定常系统 0 5 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0 5 -1 -0.5 0 0.5 1 1.5 2 0 5 -2 -1 0 1 2 3 4 5 Step Response Time (sec) Amplitude Impulse Response Time (sec) Amplitude Response to Initial Conditions Time (sec) Amplitude 图2-2 单输入—单输出线性定常系统
现代控制理论实验 step response From h(1) From n(② 2 4 2 4 imp4nse From h(1) From (2) nise 2 4 Time (sec) 图23两输入一单输出线性定常系统 09 08 例题4: 07 a=04;-2-21: b=01'. c=[12: d-0; [y.x.t]-step(a.b.c.d). 01 x1=x(,1: x2=x,2 01 plot(t.x1.'-.r.t.x2.'-k.ty,*g) 运行结果为:如图2-4 图24单输入一单输出线性定常系统 2.用矩阵指数函数法解状态方程 例1 程序:A=01,-2-3引 B=0:1: =1: [Phit.PhitBu]=chen1(A.B.u)
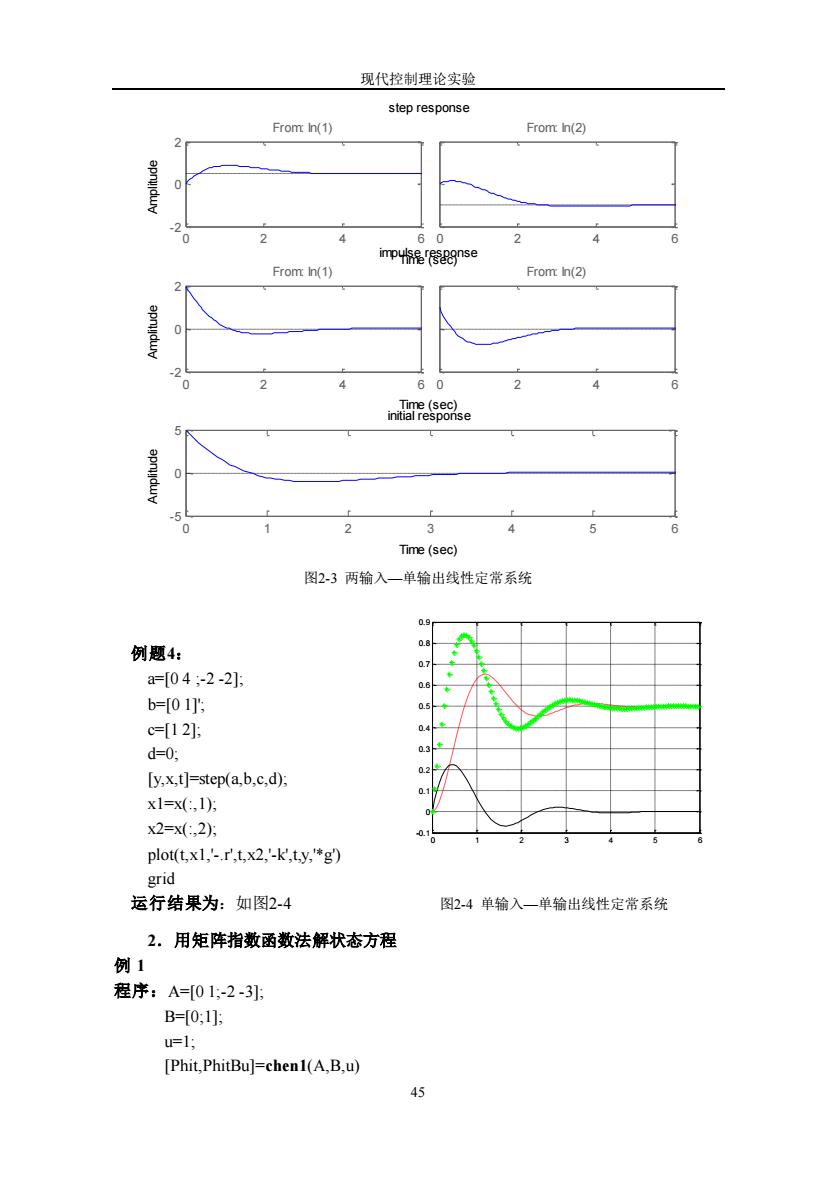
现代控制理论实验 45 0 2 4 6 - 2 0 2 From: In(1) 0 2 4 6 From: In(2) 0 2 4 6 - 2 0 2 From: In(1) 0 2 4 6 From: In(2) 0 1 2 3 4 5 6 - 5 0 5 step response Time (sec) Amplitude impulse response Time (sec) Amplitude initial response Time (sec) Amplitude 图2-3 两输入—单输出线性定常系统 例题4: a=[0 4 ;-2 -2]; b=[0 1]'; c=[1 2]; d=0; [y,x,t]=step(a,b,c,d); x1=x(:,1); x2=x(:,2); plot(t,x1,'-.r',t,x2,'-k',t,y,'*g') grid 运行结果为:如图2-4 图2-4 单输入—单输出线性定常系统 2.用矩阵指数函数法解状态方程 例 1 程序:A=[0 1;-2 -3]; B=[0;1]; u=1; [Phit,PhitBu]=chen1(A,B,u) 0 1 2 3 4 5 6 -0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9