习思 题1业1:妇图所示。两根长直导线互相平行地收置,导线内电流大小相等,均为!■10A,方向 相同,如图所示。来图中从,N两点的短球强度B的大小和方向(图中m-0020m, 年N 81 a 恩1心2:已知地球业极地场延够强度B的大小为60x103T。如设塑此地磁场是由她球赤道上 一圆电流所激发的(如图所示),此电流有多大?流向如阿? 题10.3:如图所示,载流导线在平面内分布,电流为山它在点O的腿多强度为多少: a 题1Q如图所示,率轻为R的木球上接有密集的细导线,线围平面腹此平行,几以单层线圈 夏盖住率个球面。设线图的总更数为,通过线图的电黄为了,求球心O处的磁感强度, 题1业5:实验中常用所谓的变姆霜兹线圈在局 区域内获得一近似均匀的型场,其装置简围 如图所示,一对完全相同、被此平行的线圈, 它门的半径均为是。通过的电流均为上,且两 线圈中电麓的流向相同。试证,当两线圈中心 之间的距离d等于线圆的米径R时,在两线圈 中心连线的中点附近区域,避场可看成是均匀 磁场,〔提示:如以两线图中心为坐标原点O, a 两线圈中心连线为x轴,则中点财近的城场可 看成是均匀延场的条件为 d 0)
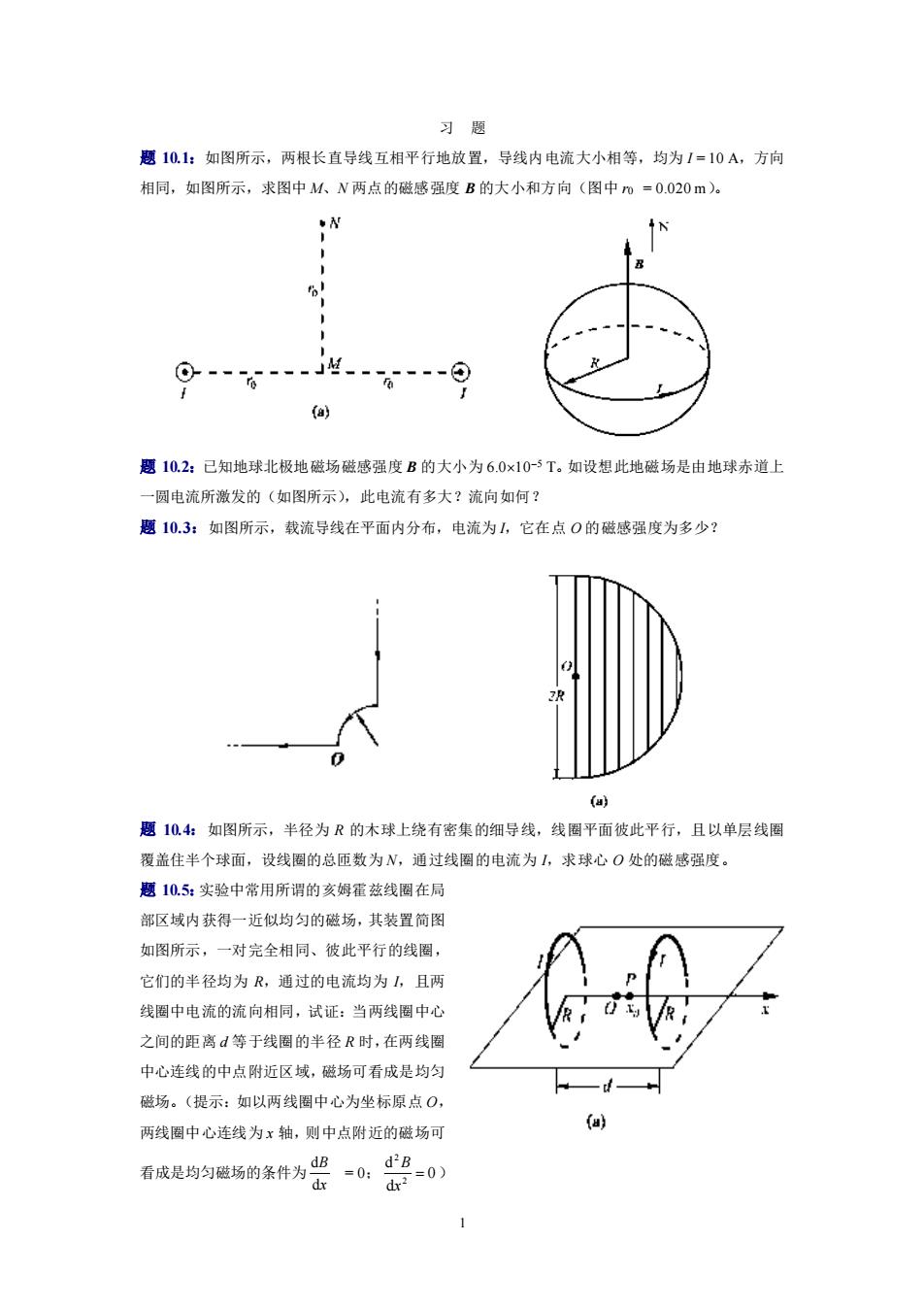
1 习 题 题 10.1:如图所示,两根长直导线互相平行地放置,导线内电流大小相等,均为 I = 10 A,方向 相同,如图所示,求图中 M、N 两点的磁感强度 B 的大小和方向(图中 r0 = 0.020 m)。 题 10.2:已知地球北极地磁场磁感强度 B 的大小为 6.010−5 T。如设想此地磁场是由地球赤道上 一圆电流所激发的(如图所示),此电流有多大?流向如何? 题 10.3:如图所示,载流导线在平面内分布,电流为 I,它在点 O 的磁感强度为多少? 题 10.4:如图所示,半径为 R 的木球上绕有密集的细导线,线圈平面彼此平行,且以单层线圈 覆盖住半个球面,设线圈的总匝数为 N,通过线圈的电流为 I,求球心 O 处的磁感强度。 题 10.5:实验中常用所谓的亥姆霍兹线圈在局 部区域内获得一近似均匀的磁场,其装置简图 如图所示,一对完全相同、彼此平行的线圈, 它们的半径均为 R,通过的电流均为 I,且两 线圈中电流的流向相同,试证:当两线圈中心 之间的距离 d 等于线圈的半径 R 时,在两线圈 中心连线的中点附近区域,磁场可看成是均匀 磁场。(提示:如以两线圈中心为坐标原点 O, 两线圈中心连线为 x 轴,则中点附近的磁场可 看成是均匀磁场的条件为 x B d d = 0; 0 d d 2 2 = x B )
想10,6,如图所示,载流长直导找的电流为人。试求通过距形面积的磁通量。 a 题1山7:如图所示,在够强瘦为B的均匀磁场中,有一半轻为R的半球面,B与半球面轴线 的夹角为@,求通过该半球面的磁通量。 题1L8已知10m世视铜线允许通过50A电流而不金使导线过热,电流在导规横戴面上均匀 分布。浅:(1)导线内,外题感强度的分布:(2)导找表面的磁够强度。 题1外有一同轴电境。其尺寸如图所示。两导棒中的电流均为,但电流的流向图反,导体的 磁性可不考虑。试计算以下各处的@感强度:(1)<R:(2)RR:(3)R4:《4)PR: 面出B一r图线: 倒 题11如图所示,N匝线圈均匀密绕在截面为长方彩的中空骨架上,求通入电流I后,环内 外磁场的分布。 题1血11:设有两无限大平行载流平面,它们的电流密度均为小电流流向相反,如图所示,求: (1)两载流平面之间的磁多强度:(2》两面之外空间的磁感强度。 U- 恩112:测定离子颜量的质谱仪如图所示,离子源S产生顺最为m。电背为g的离子。离子的 初速很小,可看作是静止的,经电势差如速后离子速入融感强度为B的均幻融场,并沿一率 2
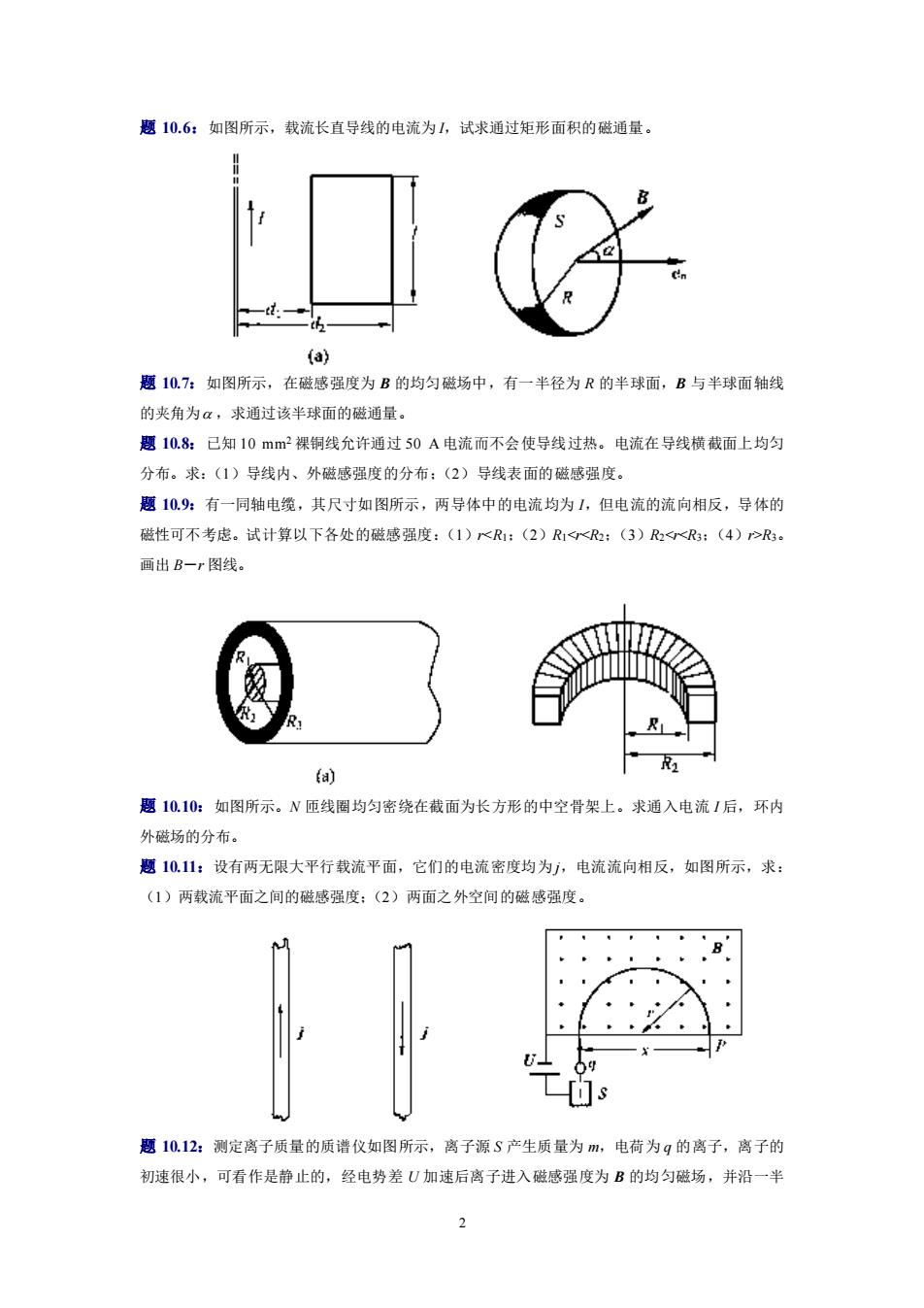
2 题 10.6:如图所示,载流长直导线的电流为 I,试求通过矩形面积的磁通量。 题 10.7:如图所示,在磁感强度为 B 的均匀磁场中,有一半径为 R 的半球面,B 与半球面轴线 的夹角为 ,求通过该半球面的磁通量。 题 10.8:已知 10 mm2 裸铜线允许通过 50 A 电流而不会使导线过热。电流在导线横截面上均匀 分布。求:(1)导线内、外磁感强度的分布;(2)导线表面的磁感强度。 题 10.9:有一同轴电缆,其尺寸如图所示,两导体中的电流均为 I,但电流的流向相反,导体的 磁性可不考虑。试计算以下各处的磁感强度:(1)r<R1;(2)R1<r<R2;(3)R2<r<R3;(4)r>R3。 画出 B-r 图线。 题 10.10:如图所示。N 匝线圈均匀密绕在截面为长方形的中空骨架上。求通入电流 I 后,环内 外磁场的分布。 题 10.11:设有两无限大平行载流平面,它们的电流密度均为 j,电流流向相反,如图所示,求: (1)两载流平面之间的磁感强度;(2)两面之外空间的磁感强度。 题 10.12:测定离子质量的质谱仪如图所示,离子源 S 产生质量为 m,电荷为 q 的离子,离子的 初速很小,可看作是静止的,经电势差 U 加速后离子进入磁感强度为 B 的均匀磁场,并沿一半
周形轨道到达离入口处距离为x的感光底片上,试证明连高子的质量为 8'4x 题113己知地面上空某处地做场的碱感登度B=04×104T,方向向北。若学宙射线中有一 速率r■50x10m:s的顺子。垂直地通过该处。如图所示,求:(1洛伦弦力的方向:2)洛伦 燕力的大小,并与该质子受到的万有引力相比较: B 恩1川14:在一个显檬管的电子束中,电子有12×10V的能量,这个显檬管安放的位置桂电子 水平地由南向北运动。地球磁场的垂直分量B.=55×0$T,并且方向向下。求:电子束偏 转方向:2)电子束在是锋管内通过20cm到达解由时光点的偏转间距: 题1015如图所示。设有一质量为m的电子射 入壁感强瘦为B的均匀磁场中,当它位于点时, 具有与慰场方向成:角的速度,它都螺餐线运动 一周到达点N,试证从,W两点间的距离为 MV2mroosa eB 题1业16:利用密耳元件可以测量硫场的磁感强度。设一需耳元件用金属材料制成,其厚度为015 mm。载流子数密度为1.0×104m一。将霍耳元件放入待测磁场中,测得霍耳电压为42V,电 流为10mA。求此时待测磁场的磁感强度。 题10.17:试证明霍耳电场强度与稳恒电场强度之比 Eu /Ee -BImep 这里为材料电阻省,n为靓液子的数密度。 恩1山18:载流子浓度是率导体材料的重要参数,工艺 上通过拉制三价或五价排柔厚子的沫度,来控制P型 或型华导体的载流子浓度,利用霍耳效应可以测量 规流子的末度和类型,如图所示一块半导体材料样品, 均匀磁场垂直于样品表面,样品中通过的电流为,我 测得霍耳电压为州,证明样品载黄子浓度为 B
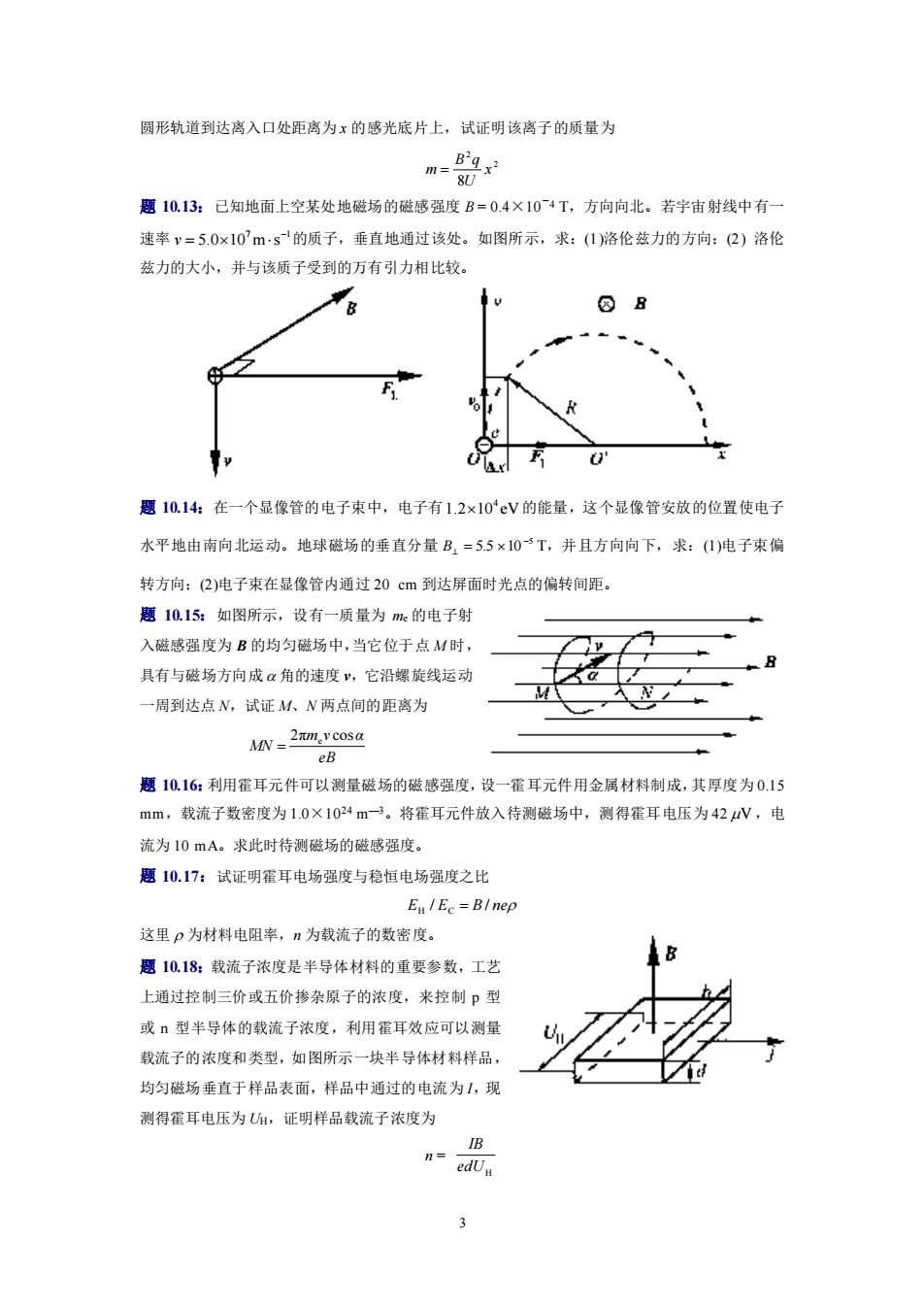
3 圆形轨道到达离入口处距离为 x 的感光底片上,试证明该离子的质量为 2 2 8 x U B q m = 题 10.13:已知地面上空某处地磁场的磁感强度 B = 0.4×10-4 T,方向向北。若宇宙射线中有一 速率 7 1 5.0 10 m s − v = 的质子,垂直地通过该处。如图所示,求:(1)洛伦兹力的方向;(2) 洛伦 兹力的大小,并与该质子受到的万有引力相比较。 题 10.14:在一个显像管的电子束中,电子有 1.2 10 eV4 的能量,这个显像管安放的位置使电子 水平地由南向北运动。地球磁场的垂直分量 5 5.5 10 − B⊥ = T,并且方向向下,求:(1)电子束偏 转方向;(2)电子束在显像管内通过 20 cm 到达屏面时光点的偏转间距。 题 10.15:如图所示,设有一质量为 me 的电子射 入磁感强度为 B 的均匀磁场中,当它位于点 M 时, 具有与磁场方向成 角的速度 v,它沿螺旋线运动 一周到达点 N,试证 M、N 两点间的距离为 eB m v α MN 2π cos e = 题 10.16:利用霍耳元件可以测量磁场的磁感强度,设一霍耳元件用金属材料制成,其厚度为 0.15 mm,载流子数密度为 1.0×1024 m—3。将霍耳元件放入待测磁场中,测得霍耳电压为 42 V ,电 流为 10 mA。求此时待测磁场的磁感强度。 题 10.17:试证明霍耳电场强度与稳恒电场强度之比 EH / EC = B / ne 这里 为材料电阻率,n 为载流子的数密度。 题 10.18:载流子浓度是半导体材料的重要参数,工艺 上通过控制三价或五价掺杂原子的浓度,来控制 p 型 或 n 型半导体的载流子浓度,利用霍耳效应可以测量 载流子的浓度和类型,如图所示一块半导体材料样品, 均匀磁场垂直于样品表面,样品中通过的电流为 I,现 测得霍耳电压为 UH,证明样品载流子浓度为 n = H edU IB
题11身一通有电流为/的导线,弯成如图所示的形状,放在 碱感强度为B的均陆场中,B的方向垂直纸面向里,求此导线 受到的安绪力为多少? 题1020:一直流变电站将电医为300kV的直流电,通过两条蓝 面不计的平行输电线输向远方,已如两输电导线可单位长度的电 容为3,0×10F-m,若号线阿的静电力与安幅力正好抵清, 求:(1)通过输电战的电流:(2)输送的功率。 a 题1《:将一电流均匀分布的无限大载流平面成入磁够强度为 B的均匀壁场中,电流方向与难场垂直,敢入后,平面两侧础场 的磁感强度分别为B1和B:《图),求该线流平面上单位面积所受 的磁场力的大小和方向。 题1L22:在直径为10©m的铜棒上,切割下一个同盘,设想这 个圆盘的厚度只有一个原子线度那么大,这样在圆盘上约有 62×104个铜原予,每个铜原予有27个电子,每个电子的自旋 磁矩为从,-93×10Am2。我们假设所有电子的白能磁矩方向 都相同。且平行于啊棒的轴线,求:(1)圆盘的磁矩:(2》如这程矩是由圆盘上的电流产生的, 那么圆盘边峰上需要有多大的电流。 题1L23:通有电流山=50A的无限长直导战,放在如图所示的形线面的柏线上,线圈中的电 流左=20A,找圈高A73,乘作用在规图上的力: 题124如图所示,在一通有电流/的长直导线附近,有一半轻为R,质量为用的细小线圈, 睡小线国可绕通过其中心与直导线平行的轴转诗,直导线与闻小线圈中心相距为d,设d>R, 通过小线圈的电流为”。若开始时线圈是静止的,它的正法线矢量#,的方白与纸面法线,的方 向成队角。间线图平面转至与解存面重叠时,角速度的值为多大? 愿1025如图所承。电率为P的金属圆环,其内外半径分别为风和风,厚度为d。圆环成 入壁感强瘦为口的均匀壁场中,B的方向与圆环平面垂直,将圆环内外边缘分别接在如图所示
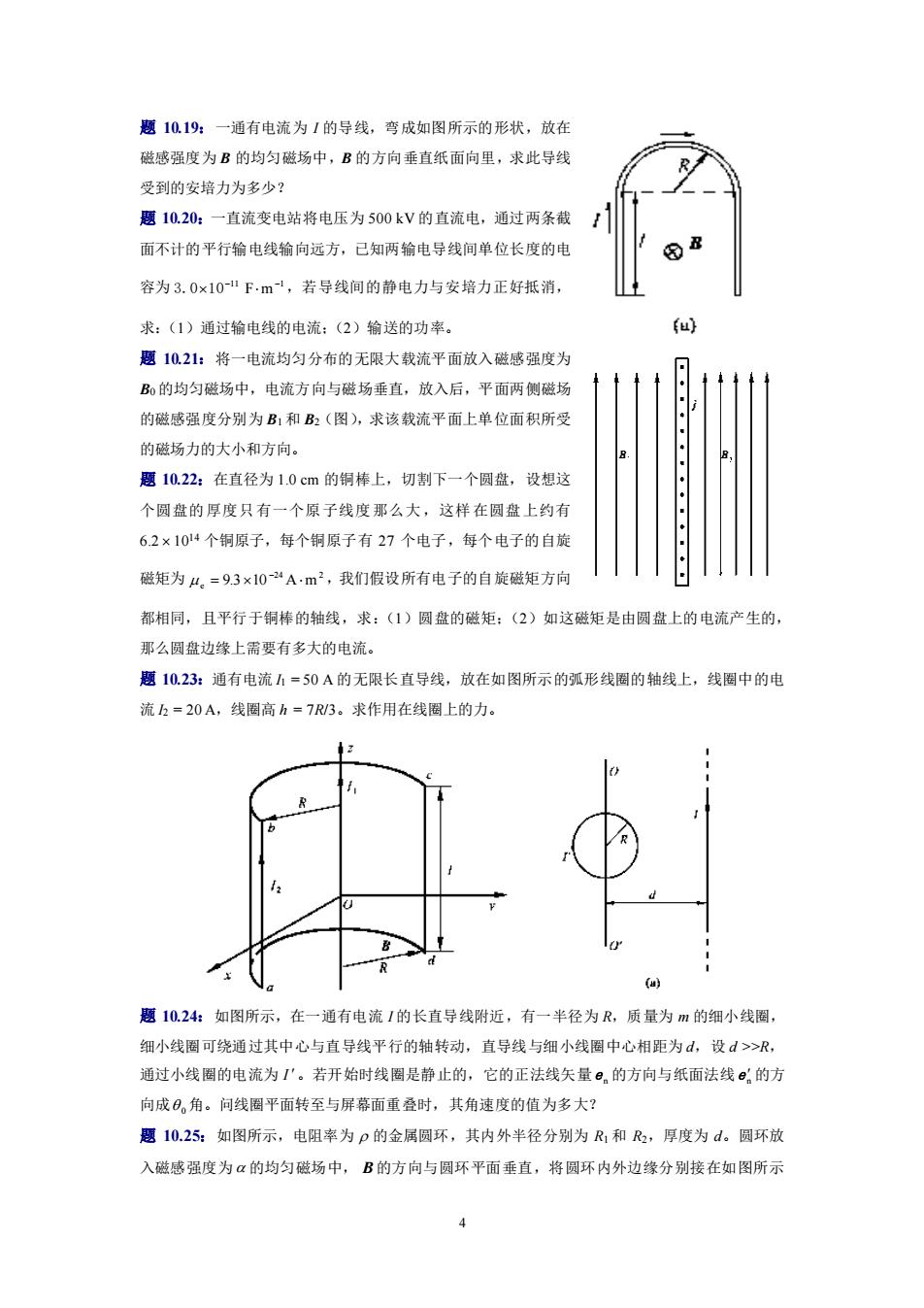
4 题 10.19:一通有电流为 I 的导线,弯成如图所示的形状,放在 磁感强度为 B 的均匀磁场中,B 的方向垂直纸面向里,求此导线 受到的安培力为多少? 题 10.20:一直流变电站将电压为 500 kV 的直流电,通过两条截 面不计的平行输电线输向远方,已知两输电导线间单位长度的电 容为 11 1 3.0 10− − Fm ,若导线间的静电力与安培力正好抵消, 求:(1)通过输电线的电流;(2)输送的功率。 题 10.21:将一电流均匀分布的无限大载流平面放入磁感强度为 B0 的均匀磁场中,电流方向与磁场垂直,放入后,平面两侧磁场 的磁感强度分别为 B1 和 B2(图),求该载流平面上单位面积所受 的磁场力的大小和方向。 题 10.22:在直径为 1.0 cm 的铜棒上,切割下一个圆盘,设想这 个圆盘的厚度只有一个原子线度那么大,这样在圆盘上约有 6.2 1014 个铜原子,每个铜原子有 27 个电子,每个电子的自旋 磁矩为 24 2 e = 9.3 10 Am − ,我们假设所有电子的自旋磁矩方向 都相同,且平行于铜棒的轴线,求:(1)圆盘的磁矩;(2)如这磁矩是由圆盘上的电流产生的, 那么圆盘边缘上需要有多大的电流。 题 10.23:通有电流 I1 = 50 A 的无限长直导线,放在如图所示的弧形线圈的轴线上,线圈中的电 流 I2 = 20 A,线圈高 h = 7R/3。求作用在线圈上的力。 题 10.24:如图所示,在一通有电流 I 的长直导线附近,有一半径为 R,质量为 m 的细小线圈, 细小线圈可绕通过其中心与直导线平行的轴转动,直导线与细小线圈中心相距为 d,设 d >>R, 通过小线圈的电流为 I 。若开始时线圈是静止的,它的正法线矢量 e n 的方向与纸面法线 e n 的方 向成 0 角。问线圈平面转至与屏幕面重叠时,其角速度的值为多大? 题 10.25:如图所示,电阻率为 的金属圆环,其内外半径分别为 R1 和 R2,厚度为 d。圆环放 入磁感强度为 的均匀磁场中, B 的方向与圆环平面垂直,将圆环内外边缘分别接在如图所示

的电动势为x的电源两极。圆环可绕通过环心乐直环面的轴转动,求圆环所受的磁力矩。 a 题12制如图所承,常径为R的圆片均匀带电,电荷面密度为口,令该到片以角速度。绕通 过其中心且垂直于圆平面的轴旋转。求轴战上距网片中心为¥处的点P的融感强度和旋转圆片 的姬矩。 题10,27:如图所示是一种正在研究中的电磁物道炮的原理图。该装置可用于发射速度高达0 kms的烛弹,超弹置于两条平行轨道之间与轨道相接触。轨道是半径为r的圆性形导体,轨道 间距为d。饱弹沿轨道可以自由滑动。何流电界£、饱弹和轨道构成一团合回路,回路中电流为 1(1》正明作用在炮辣上的赋场力为 F=42 (2)假设/=4300kA,d=20■m,7=67cm,烟弹从静止起经过一段路程L=4.0m知速日 的速度为多大?(设炮弹质量网一100kg) 5
5 的电动势为 的电源两极,圆环可绕通过环心垂直环面的轴转动,求圆环所受的磁力矩。 题 10.26:如图所示,半径为 R 的圆片均匀带电,电荷面密度为 ,令该圆片以角速度 绕通 过其中心且垂直于圆平面的轴旋转。求轴线上距圆片中心为 x 处的点 P 的磁感强度和旋转圆片 的磁矩。 题 10.27:如图所示是一种正在研究中的电磁轨道炮的原理图。该装置可用于发射速度高达 10 km.s-1 的炮弹,炮弹置于两条平行轨道之间与轨道相接触,轨道是半径为 r 的圆柱形导体,轨道 间距为 d。炮弹沿轨道可以自由滑动。恒流电源 、炮弹和轨道构成一闭合回路,回路中电流为 I。(1)证明作用在炮弹上的磁场力为 r μ I d r F + = )ln π ( 2 1 2 0 (2)假设 I = 4 500 kA,d = 120 mm,r = 6.7 cm,炮弹从静止起经过一段路程 L = 4.0 m 加速后 的速度为多大?(设炮弹质量 m = 10.0 kg)