
愿41:一汽车发动机曲轴的转速在12s内由12×10'r:mm均匀的增如到27×0'r·m。 (1)求曲轴转动的角加速度:(2)在此时间内,曲轴转了多少转? 题41解,(1)由于角速度。=2别(n为单位时间内的轮数),根据角加速度的定义a=如 在匀麦速转动中角加速度为 a=-4=2-l=131g (2》发动机曲拍过的角度为 0=aw+m2=21=0+r 2 在128内由轴转过的圈数为 N-日.0+1-30圈 22 题42上某种电动机启动后转速随时间变化的关系为0=。-e),式中。-90md·s, r=20s。求:(1)1=60s时的转速:(2)角加速度随时间变化的规律,(3)启动后6.0s内 转过的圈数。 恩42解:(1)根据盟意中转速随时间的变化关系。将1=6.0s代入,即得 (2》角加速度随时间变化的规律为 a-p.4.4 (3)1=6.0s时转过的角度为 -o-f:'mi--xond 则1=6.0s时电动机转过的圈数 N-日-57图 2开 思43:如图所示,一通风机的转动部分以初角速度。,烧其轴转动,空气的阻力矩与角速度 成正比。比例系数C为一常量,若转动部分对其伯的转动惯量为」,月:《1)经过多少时间 后其转动角速度减少为初角速度的一半?(2)在此时间内共转过多少转? 题43解:(1)通风机叶片所受的阻力矩为M=-C,由转动定律M=知,可得叶片的角 加速度为 a=p=-Ce(1) d山 根据初始条件对式《1)积分,有 出- 由于C和J均为常量,得
题 4.1:一汽车发动机曲轴的转速在 12 s 内由 3 1 1.2 10 r min − 均匀的增加到 3 1 2.7 10 r min − 。 (1)求曲轴转动的角加速度;(2)在此时间内,曲轴转了多少转? 题 4.1 解:(1)由于角速度 =2n(n 为单位时间内的转数),根据角加速度的定义 dt d = , 在匀变速转动中角加速度为 ( ) 0 0 2 13.1 rad s 2 − = − = − = t n n t (2)发动机曲轴转过的角度为 t t t (n n )t 0 2 0 0 2 2 1 = + + = + = 在 12 s 内曲轴转过的圈数为 390 圈 2 2 0 = + = = t n n N 题 4.2:某种电动机启动后转速随时间变化的关系为 (1 ) 0 t e − = − ,式中 1 0 9.0 rad s − = , = 2.0 s 。求:(1) t = 6.0 s 时的转速;(2)角加速度随时间变化的规律;(3)启动后 6.0 s 内 转过的圈数。 题 4.2 解:(1)根据题意中转速随时间的变化关系,将 t = 6.0 s 代入,即得 1 0 0 1 0.95 8.6 s − − = = = − t e (2)角加速度随时间变化的规律为 0 2 2 4.5 s d d − − − = = = t t e e t (3)t = 6.0 s 时转过的角度为 d 1 d 36.9 rad 6 0 0 6 0 = = = − s − t s t e t 则 t = 6.0 s 时电动机转过的圈数 5.87 圈 2 = = N 题 4.3:如图所示,一通风机的转动部分以初角速度 0 绕其轴转动,空气的阻力矩与角速度 成正比,比例系数 C 为一常量。若转动部分对其轴的转动惯量为 J ,问:(1)经过多少时间 后其转动角速度减少为初角速度的一半?(2)在此时间内共转过多少转? 题 4.3 解:(1)通风机叶片所受的阻力矩为 M = −Cω ,由转动定律 M = Jα ,可得叶片的角 加速度为 J C t = = − d d (1) 根据初始条件对式(1)积分,有 = − 0 0 d d d t t J C t 由于 C 和 J 均为常量,得

aane 当角速度由气→岛,时,转动所需的时问为 1=n2 (2)服据初始条件对式(2)积分,有 Jd0-JoeTa 即 0:是 在时间:内所转过的图数为 x.0.@ “新 题44:一燃气轮机在试车时,燃气作用在锅轮上的力矩为2.心×0'N:m,祸轮的转动惯量 为250kg■2。当轮的转速由2知x10'rmm4增大到1.12x10rm时,所经历的时间为 多少? 题44解在匀变速转动中,角加速度红-包-鸟,由轮动定律M=a,可得飞轮所经历 的时间 1-0-色j-2-风)-085 解2:飞轮在恒外力矩作用下,根据角动量定理,有 灿-o-) 则 1=”=-小08 题45:用落体观察法测定飞轮的其动顺量,是将半径为R的飞轮支承在O点上,然后在绕 过飞轮的蝇子的一端挂一场量为m的重物,令重物以初速度为零下落,带动飞轮转动,记下 重物下落的距离和时间,就可算出飞轮的转动惯量。试写出它的计算式。(假设轴承闻无摩 擦) 恩4.5解1:设绳子的拉力为F,对飞轮而言,根据转动定律。有 FR-Ja 而对重物而言,由牛顿定律,有 限-=面(2) 由于绳子不可伸长,因此,有 77777777 a=R在(3》 重物作匀如速下落,则有 h-ar (4) 2
t J C e − =0 当角速度由 0 0 2 1 → 时,转动所需的时间为 ln 2 C J t = (2)根据初始条件对式(2)积分,有 − = t t J C e t 0 0 0 d d 即 C J 2 0 = 在时间 t 内所转过的圈数为 C J N 2 4 0 = = 题 4.4:一燃气轮机在试车时,燃气作用在涡轮上的力矩为 2.03 10 N m 3 ,涡轮的转动惯量 为 2 25.0 kg m 。当轮的转速由 3 1 2.80 10 r min − 增大到 4 1 1.12 10 r min − 时,所经历的时间为 多少? 题 4.4 解 1:在匀变速转动中,角加速度 t 0 − = ,由转动定律 M = Jα ,可得飞轮所经历 的时间 ( ) 10.8 s 2 0 0 = − = − = n n M J J M t 解 2:飞轮在恒外力矩作用下,根据角动量定理,有 ( ) 0 0 d = − M t J t 则 ( ) 10.8 s 2 0 0 = − = − = n n M J J M t 题 4.5:用落体观察法测定飞轮的转动惯量,是将半径为 R 的飞轮支承在 O 点上,然后在绕 过飞轮的绳子的一端挂一质量为 m 的重物,令重物以初速度为零下落,带动飞轮转动,记下 重物下落的距离和时间,就可算出飞轮的转动惯量。试写出它的计算式。(假设轴承间无摩 擦) 题 4.5 解 1:设绳子的拉力为 FT,对飞轮而言,根据转动定律,有 FTR = J 而对重物而言,由牛顿定律,有 mg − FT = ma (2) 由于绳子不可伸长,因此,有 a = R (3) 重物作匀加速下落,则有 2 2 1 h = at (4)

由上述各式可解得飞轮的转动惯量为 层-到 解2:根据系统的机械能守恒定律,有 -e+m2+w=0r 2 而线速度和角速度的关系为 T=R信(2') 又根据重物作匀如速运动时,有 v=u(岁) 2=2() 由上述各式可得 m-可 若轴承处存在厚擦,上述测量转动惯量的方法仍可采用。这时,只雷通过用两个不同质 量的置物做两次测量即可消除摩擦力矩蒂米的影响。 题46:一飞轮由一直径为0cm,厚度为2.0em的属盘和两个直径为10cm,长为80em的 共轴圆柱体组成,设飞轮的密度为78×0g·m,求飞轮对轴的转动领量。 恩46解:根据转动惯量的叠如性,由匀质圆盘、圆桂 体对轴的转动赞量公式可得 =+=* 题47:如图所示,圆世的质量为m,半径为R。求它对O轴(即通过属盘边峰且平行于 盘中心轴)的转动惯量。 题47解:根据平行轴定理J。一J。◆m成和绕圆盘中心轴0的 转动惯量。一2m?可符 g-+威. 题《多试证明质量为网,半径为R的均匀球体,以直径为转轴的转动惯量为服'。如以 和球体相切的线为轴。其转动惯量又为多少? 题4,8延:如图所示,图中阴影部分的小圆盘对OO轴的转动榄量为 w-ro-e-he-rh
由上述各式可解得飞轮的转动惯量为 = −1 2 2 2 h gt J mR 解 2:根据系统的机械能守恒定律,有 0 2 1 2 1 2 2 − mgh + mv + J = (1) 而线速度和角速度的关系为 v = R (2) 又根据重物作匀加速运动时,有 v = at (3) v 2ah 2 = (4) 由上述各式可得 = −1 2 2 2 h gt J mR 若轴承处存在摩擦,上述测量转动惯量的方法仍可采用。这时,只需通过用两个不同质 量的重物做两次测量即可消除摩擦力矩带来的影响。 题 4.6:一飞轮由一直径为 30 cm ,厚度为 2.0 cm 的圆盘和两个直径为 10 cm ,长为 8.0 cm 的 共轴圆柱体组成,设飞轮的密度为 3 3 7.8 10 kg m − ,求飞轮对轴的转动惯量。 题 4.6 解:根据转动惯量的叠加性,由匀质圆盘、圆柱 体对轴的转动惯量公式可得 4 2 2 4 1 2 2 2 2 1 1 2 1 0.136 kg m 2 1 16 1 2 2 1 2 2 1 2 = = + + = + = ld ad d m d J J J m 题 4.7:如图所示,圆盘的质量为 m ,半径为 R 。求它对 OO 轴(即通过圆盘边缘且平行于 盘中心轴)的转动惯量。 题 4.7 解:根据平行轴定理 2 J O = J O + mR 和绕圆盘中心轴 O 的 转动惯量 2 O 2 1 J = mR 可得 2 2 2 2 O O 2 3 2 1 J = J + mR = mR + mR + mR 题 4.8:试证明质量为 m ,半径为 R 的均匀球体,以直径为转轴的转动惯量为 2 5 2 mR 。如以 和球体相切的线为轴,其转动惯量又为多少? 题 4.8 证:如图所示,图中阴影部分的小圆盘对 OO轴的转动惯量为 J r m (R x ) (R x )dx 2 1 d 2 1 d 2 2 2 2 2 = = − −

式中。一品为匀质球体的密度。则球体以其直径00方转 轴的转动惯量为 J-jw-ple-ra-子e 5 又由平行轴定理可得球绕O,01轴的转动惯量为 =J+m2=2m 题4身质量面密度为。的均匀矩形板。试证其对与板面垂直的,通过几何中心的拍线的转 动损量为只+b)。其中1为矩形板的长,5为它的宽。 12 题49正取如图所示坐标,在板上取一质元dw=d时: 它对与板面垂直的,通过几何中心的轴线的转动候量为 d山-2+y2d 整个矩形板对该轴的转动惯量为 J=w=∫f2+= 五a+b) 思410:如图所示,质量属=l6的实心圆柱体A,其半径为r=15m,可以绕其固定水 平轴转动,阻力忽略不计。一条轻的柔绳绕在圆柱体上,其另一端系一个质量m:-80g的 物体B。求:(1)物体由静止开始下降10s后的距离:(2)绳的张力F,· 恩4,0解:(1)分别作两物体的受力分析图。对实心柱体而言,由转动定律得 Fr-ja-imr'a (1) 对悬挂物体面言,依据牛领定律,有 -F程=思8-F=,4(2) 且F=子。又由角量与线量的关系。得 aara 解上述方程组。可得物体下落的加速度 a=2mg m,+2m 在1=1.0s时,B下落的距离为 =m=s245m 属+2m (2)由式《2)可得绳中的张力为 5=g-小-mg=92N 周十2m3 题41山:质量为四,和m:的两物体A、B分别是挂在如图所示的组合轮两端。设两轮的半径 分别为R和,两轮的转动惯量分别为J,和:,轮与轴承间、绳索与轮间的摩擦力均略去 不计,绳的质量也略去不计,试求两物体的加速度和绳的张力: 题411解:分别对两物体及组合轮作受力分析,根据质点的牛顿定律和刚体的转动定律
式中 3 4 3 R m = 为匀质球体的密度。则球体以其直径 OO为转 轴的转动惯量为 ( ) 2 2 2 2 5 2 d 2 1 J dJ R x x mR R R = = − = − 又由平行轴定理可得球绕 O1O1 轴的转动惯量为 2 2 5 7 J = J + mR = mR 题 4.9:质量面密度为 的均匀矩形板,试证其对与板面垂直的,通过几何中心的轴线的转 动惯量为 ( ) 12 2 2 lb l + b 。其中 l 为矩形板的长, b 为它的宽。 题 4.9 证:取如图所示坐标,在板上取一质元 dm =dxdy , 它对与板面垂直的,通过几何中心的轴线的转动惯量为 dJ (x y ) dxdy 2 2 = + 整个矩形板对该轴的转动惯量为 ( ) ( ) − − = = + = + 2 2 2 2 2 2 2 2 12 1 J d d d l l b J b x y x y lb l b 题 4.10:如图所示,质量 m1 =16 kg 的实心圆柱体 A ,其半径为 r =15 cm ,可以绕其固定水 平轴转动,阻力忽略不计。一条轻的柔绳绕在圆柱体上,其另一端系一个质量 m2 = 8.0 kg 的 物体 B 。求:(1)物体由静止开始下降 1.0 s 后的距离;(2)绳的张力 FT 。 题 4.10 解:(1)分别作两物体的受力分析图。对实心圆柱体而言,由转动定律得 2 T 1 2 1 F r = J = m r (1) 对悬挂物体而言,依据牛顿定律,有 P2 − FT = m2 g − FT = m2a (2) 且 FT FT = 。又由角量与线量的关系,得 a = r 解上述方程组,可得物体下落的加速度 1 2 2 2 2 m m m g a + = 在 t = 1.0 s 时,B 下落的距离为 2.45 m 2 2 1 1 2 2 2 2 = + = = m m m gt s at (2)由式(2)可得绳中的张力为 ( ) 39.2 N 1 2 2 1 2 = + = − = g m m m m FT m g a 题 4.11:质量为 m1 和 m2 的两物体 A、B 分别悬挂在如图所示的组合轮两端。设两轮的半径 分别为 R 和 r ,两轮的转动惯量分别为 1 J 和 2 J ,轮与轴承间、绳索与轮间的摩擦力均略去 不计,绳的质量也略去不计。试求两物体的加速度和绳的张力。 题 4.11 解:分别对两物体及组合轮作受力分析,根据质点的牛顿定律和刚体的转动定律
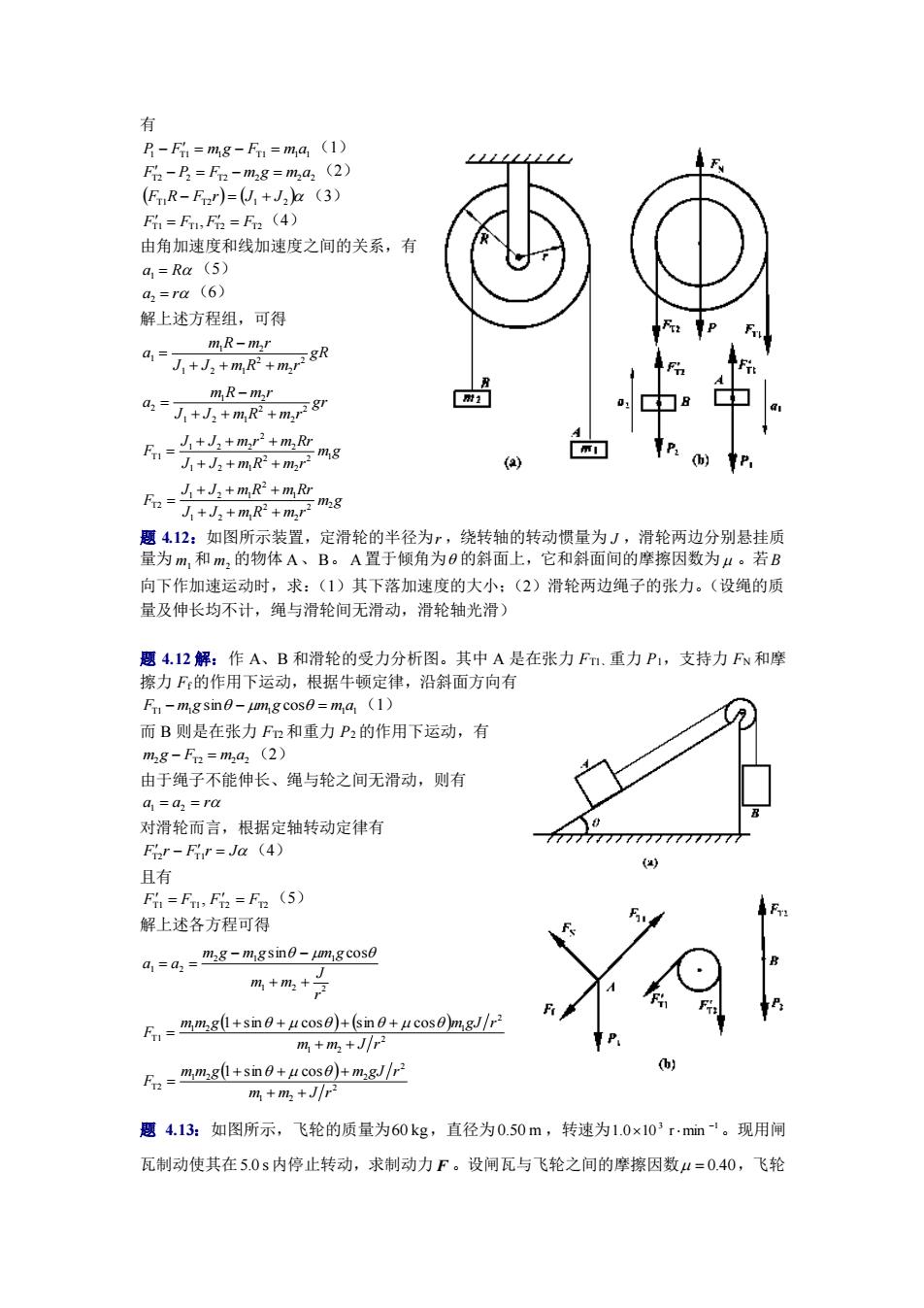
有 -=mg-F,=m4(1) 名-月=F-周8=m4(2) (ER-F小-+z(3) 吊=F=F(4) 由角加速度和线加速度之间的关系。有 4=Ra(5) 马=rg(6) 解上述方程组,可得 展R一图F +人*所用+他了8吸 ■ 思R=出,P 品“++及+周了 ,=++m2+m心 +人+网母+网子8 器 题412:如图所示装置,定滑轮的半径为r,饶转轴的转动惯量为J,滑轮两边分别悬挂质 量为围,和m的物体A、B。A置于顿角为的斜面上,它和斜面间的摩摄因数为丛·若B 向下作如速运动时,求:()其下落如速度的大小:(2》滑轮两边绳子的张力,(设绳的质 量及伸长均不计,绳与带轮间无滑动。滑轮轴光滑) 题4,12解:作A,B和滑轮的受力分析图。其中A是在张力F.重力P:支持力Fx和摩 擦力FP的作用下运动,根据牛顿定律,沿斜面方向有 F-周gsnB-%g88=mA(1) 而B则是在张力F?和重力P:的作用下运动,有 mg-=周4(2) 由干绳子不能伸长、绳与轮之间无滑动,则有 4=马-a 对滑轮而言,根据定轴转动定律有 F-F=a(4) 且有 =Fn.F品=Fm(5) 解上述各方程可得 马-4,-您8-mg5h0-四gs0 两+网+ F-mg+sn0+pcoso)+(sn+ucos0m 码+吗+ Fa-画+m9+2cs+画利止 群◆所*JP 题4,1为如图所示,飞轮的质量为60kg,直径为050m,转速为1.0×0'-m。现用闸 瓦制动使其在50s内停止转动,求制动力F。设闸瓦与飞轮之间的摩擦因数以=040,飞轮
有 P1 FT1 = m1g − FT1 = m1a1 − (1) FT2 − P2 = FT2 − m2 g = m2a2 (2) (FT1R − FT2r) = (J1 + J 2 ) (3) T1 T1 T2 T2 F = F , F = F (4) 由角加速度和线加速度之间的关系,有 a1 = R (5) a2 = r (6) 解上述方程组,可得 gR J J m R m r m R m r a 2 2 2 1 2 1 1 2 1 + + + − = gr J J m R m r m R m r a 2 2 2 1 2 1 1 2 2 + + + − = m g J J m R m r J J m r m Rr F 2 1 2 2 1 2 1 2 2 1 2 2 T1 + + + + + + = m g J J m R m r J J m R m Rr F 2 2 2 2 1 2 1 1 2 1 2 1 T2 + + + + + + = 题 4.12:如图所示装置,定滑轮的半径为 r ,绕转轴的转动惯量为 J ,滑轮两边分别悬挂质 量为 m1 和 m2 的物体 A、B。 A 置于倾角为 的斜面上,它和斜面间的摩擦因数为 。若 B 向下作加速运动时,求:(1)其下落加速度的大小;(2)滑轮两边绳子的张力。(设绳的质 量及伸长均不计,绳与滑轮间无滑动,滑轮轴光滑) 题 4.12 解:作 A、B 和滑轮的受力分析图。其中 A 是在张力 FT1、重力 P1,支持力 FN 和摩 擦力 Ff的作用下运动,根据牛顿定律,沿斜面方向有 T1 1 1 1 1 F − m g sin − m g cos = m a (1) 而 B 则是在张力 FT2 和重力 P2 的作用下运动,有 m2 g − FT2 = m2a2 (2) 由于绳子不能伸长、绳与轮之间无滑动,则有 a1 = a2 = r 对滑轮而言,根据定轴转动定律有 FT2 r − FT1 r = J (4) 且有 T1 T1 T2 T2 F = F , F = F (5) 解上述各方程可得 1 2 2 2 1 1 1 2 sin cos r J m m m g m g m g a a + + − − = = ( ) ( ) 2 1 2 2 1 2 1 T1 1 sin cos sin cos m m J r m m g m gJ r F + + + + + + = ( ) 2 1 2 2 1 2 2 T2 1 sin cos m m J r m m g m gJ r F + + + + + = 题 4.13:如图所示,飞轮的质量为 60 kg ,直径为 0.50 m ,转速为 3 1 1.0 10 r min − 。现用闸 瓦制动使其在 5.0 s 内停止转动,求制动力 F 。设闸瓦与飞轮之间的摩擦因数 = 0.40 ,飞轮