
例7.计算心形线r=a(1+cos0)(a>0)与圆r=a 所围图形的面积 解:利用对称性,所求面积 4-2() x2+a月+2cas0t2cos20d0 y 2+a-2) 2ax -2a2 HIGH EDUCATION PRESS ©-色0C①8 机动目录上页下页返回结束
2 1+ 2cos + cos (1 cos 2 ) 2 1 + o a 2a x y (1 cos ) d 2 1 2 2 + a 例7. 计算心形线 与圆 所围图形的面积 . 解: 利用对称性 , + 2 2 2 1 A = a = + 2 2 2 1 a a cos 2 )d 2 1 2cos 2 3 ( + + 所求面积 2) 4 3 ( 2 1 2 2 = a + a − 机动 目录 上页 下页 返回 结束

例8.求双纽线 ,2=a2cos20所围图形面积 解:利用对称性,则所求面积为 4=43a2cos2d =a2j4cos29d(20) a2(sin20]=a2 思考:用定积分表示该双纽线与圆 所围公共部分的面积 答案: HIGH EDUCATION PRESS 机动目录上页下页返回结束
a sin 2 2 = a 例8. 求双纽线 所围图形面积 . 解: 利用对称性 , cos2 d 2 1 2 a = 4 0 2 a cos 2 d (2 ) 则所求面积为 2 = a 思考: 用定积分表示该双纽线与圆 所围公共部分的面积 . 机动 目录 上页 下页 返回 结束 答案:

二、平面曲线的弧长 定义:若在弧B上任意作内接折线,当折线段的最大 边长入→0时,折线的长度趋向于一个确定的极限,则称 此极限为曲线弧AB的弧长,即 s lim 20 并称此曲线弧为可求长的 定理:任意光滑曲线弧都是可求长的 (证明略) HIGH EDUCATION PRESS D-C①8 机动目录上页下页返回结束
二、平面曲线的弧长 定义: 若在弧 AB 上任意作内接折线 , Mi−1 当折线段的最大 边长 →0 时, 折线的长度趋向于一个确定的极限 , 此极限为曲线弧 AB 的弧长 , 即 并称此曲线弧为可求长的. 定理: 任意光滑曲线弧都是可求长的. (证明略) 0 lim → = s 机动 目录 上页 下页 返回 结束 则称
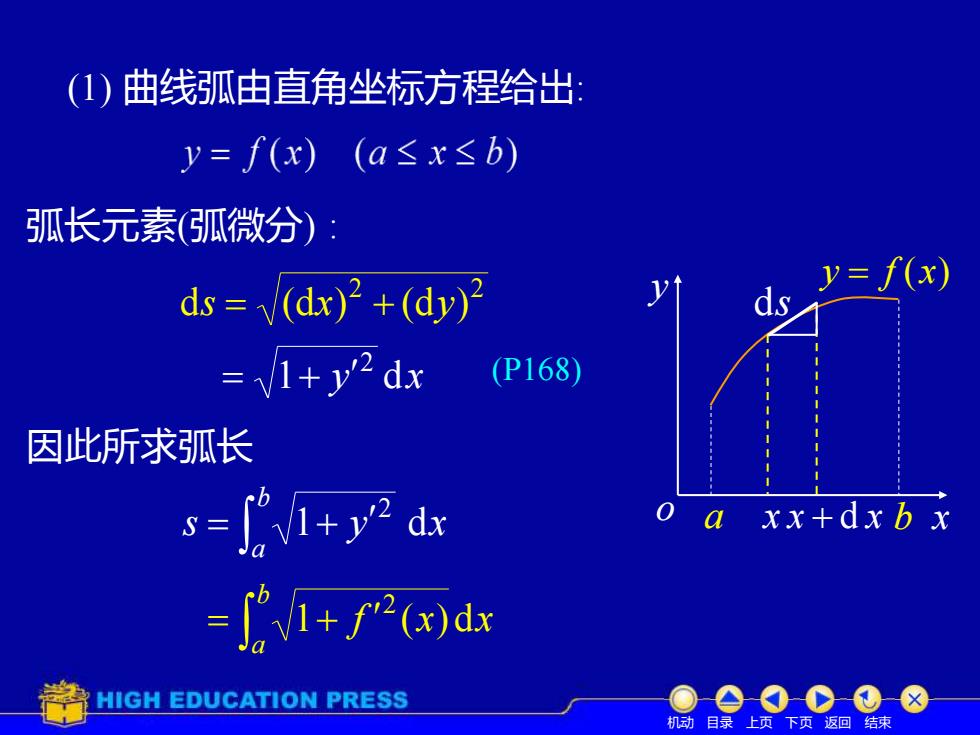
(1)曲线弧由直角坐标方程给出 y=f(x)(a≤x≤b) 弧长元素(弧微分): ds=√(dx2+(dy) y=f(x) v1+y'2 dx (P168) 因此所求弧长 s=f+y2 dx o a xx+dxb x =∫1+f(x)dx HIGH EDUCATION PRESS 几动目录上页下页返回结束
ds y o a b x (1) 曲线弧由直角坐标方程给出: y = f (x) 弧长元素(弧微分) : x x + d x 1 y dx 2 = + 因此所求弧长 s y x b a 1 d 2 = + f x x b a 1 ( ) d 2 = + (P168) 2 2 ds = (dx) + (dy) 机动 目录 上页 下页 返回 结束

(2)曲线弧由参数方程给出: -o9 弧长元素(弧微分): ds =v(dx)2+(dy)2 =Vo2(0)+y2()d 因此所求弧长 s=o2)+w2(0)d1 HIGH EDUCATION PRESS 机动目录上页下页返回结束
(2) 曲线弧由参数方程给出: 弧长元素(弧微分) : 因此所求弧长 s (t) (t) dt 2 2 = + (t) (t) dt 2 2 = + 2 2 ds = (dx) + (dy) 机动 目录 上页 下页 返回 结束