
导航 2)经验回归直线一定经过样本点的中心(,习), (3)经验回归方程中的截距α和斜率b都是通过样本估计得来的,存 在误差,这种误差可能导致预测结果的偏差 (4)经验回归方程y=a+x中的b表示x每增加1个单位时预测 值y的平均变化量,而α表示预测值y不随x的变化而变化的部分
导航 (2)经验回归直线一定经过样本点的中心(𝒙, 𝒚). (3)经验回归方程中的截距𝒂 ^ 和斜率𝒃 ^ 都是通过样本估计得来的,存 在误差,这种误差可能导致预测结果的偏差. (4)经验回归方程𝒚 ^ = 𝒂 ^ + 𝒃 ^ x 中的𝒃 ^ 表示 x 每增加 1 个单位时预测 值𝒚 ^ 的平均变化量,而𝒂 ^ 表示预测值𝒚 ^ 不随 x 的变化而变化的部分

导 (⑤)对于建立的回归模型,我们必须对模型的拟合效果进行 分析,也就是对利用回归模型解决实际问题的效果进行评价: 一方面可以对比残差或残差平方和的大小,同时观察残差图, 进行残差分析;另一方面也可以研究数据的2(样本相关系数 ).对模型拟合效果的分析能够帮助我们利用最优化的模型来 解决实际问题
导航 (5)对于建立的回归模型,我们必须对模型的拟合效果进行 分析,也就是对利用回归模型解决实际问题的效果进行评价. 一方面可以对比残差或残差平方和的大小,同时观察残差图, 进行残差分析;另一方面也可以研究数据的R2 (样本相关系数 r).对模型拟合效果的分析能够帮助我们利用最优化的模型来 解决实际问题
导航 【典型例题1】对于x与y有如下观测数据: 18 25 30 39 41 42 49 52 5 6 7 8 8 9 10 (1)作出散点图; (2)对x与y作回归分析; 3)求出y关于x的经验回归方程; (4)根据经验回归方程,预测当=60时y的值
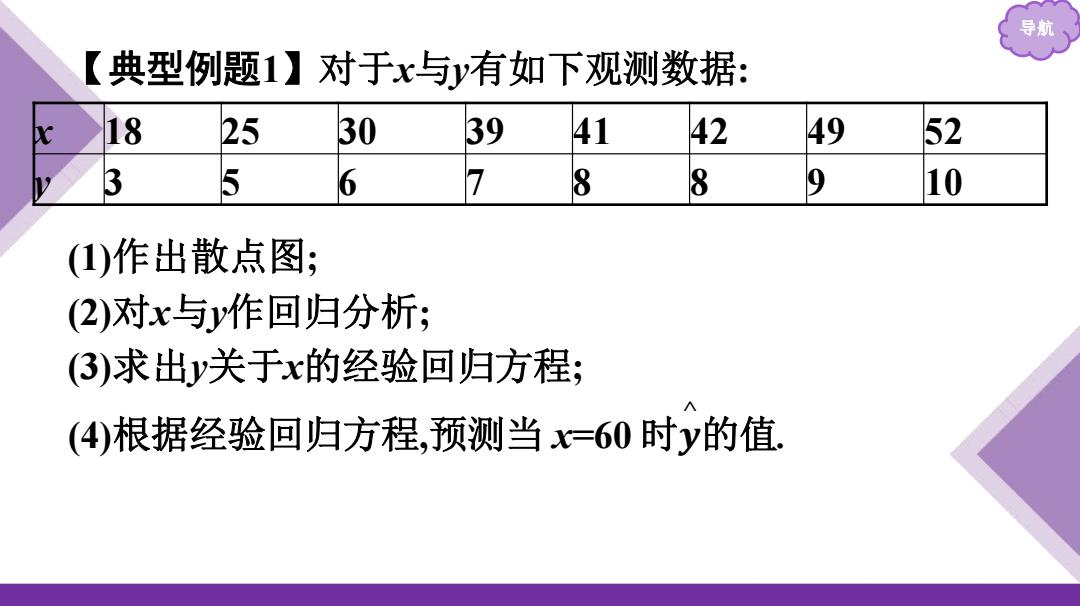
导航 【典型例题1】对于x与y有如下观测数据: x 18 25 30 39 41 42 49 52 y 3 5 6 7 8 8 9 10 (1)作出散点图; (2)对x与y作回归分析; (3)求出y关于x的经验回归方程; (4)根据经验回归方程,预测当 x=60 时𝒚 ^ 的值
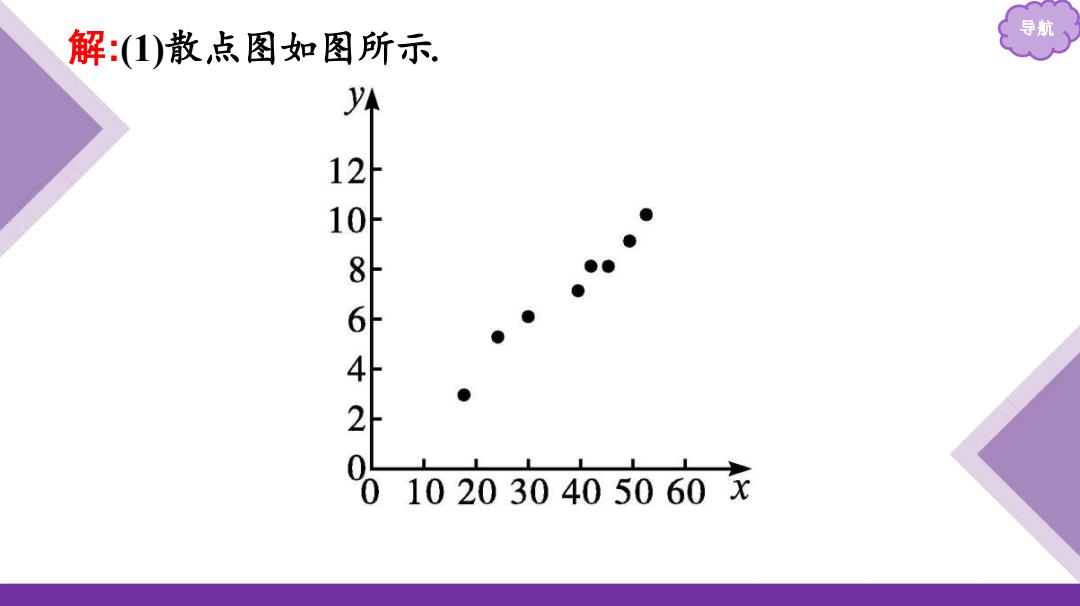
解:1)散点图如图所示 导航 个 20 8642 0 102030405060x
导航 解 :(1)散点图如图所示

(2)作相关性检验: 导航 = (18+25+30+39+41+42+49+52)296-37, 8 y=。×(3+5+6+7+8+8+9+10)=7, 8 8 182+252+3024392+412+422+492+522 8 7-32452462+72+82+82+924102-428. 8 xy=18×3+25×5+30×6+39×7+41×8+42×8+49×9+52×10=2257, i=1 含0r8x-2257-8×37×7=185
导航 (2)作相关性检验: 𝐱 = 𝟏 𝟖 ×(18+25+30+39+41+42+49+52)= 𝟐𝟗𝟔 𝟖 =37, 𝐲 = 𝟏 𝟖 ×(3+5+6+7+8+8+9+10)=7, ∑ 𝐢=𝟏 𝟖 𝒙𝒊 𝟐 =182 +252 +302 +392 +412 +422 +492 +522 =11 920, ∑ 𝒊=𝟏 𝟖 𝒚𝒊 𝟐 =3 2 +5 2 +6 2 +7 2 +8 2 +8 2 +9 2 +102 =428, ∑ 𝒊=𝟏 𝟖 xiyi=18×3+25×5+30×6+39×7+41×8+42×8+49×9+52×10=2 257, ∑ 𝒊=𝟏 𝟖 xiyi-8𝒙 𝒚=2 257-8×37×7=185