
全程设计 8.2 一元线性回归模型及其应用
8.2 一元线性回归模型及其应用
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导奥 素养·目标定位 目标素养 1.了解一元线性回归模型及随机误差、残差、残差分析的概 念 2.了解最小二乘法的思想方法,会求经验回归方程,并用回归 方程进行预报. 3.会用残差分析判断经验回归模型的拟合效果 4.了解非线性模型通过变换转化为线性回归模型的思想
导航 目 标 素 养 1.了解一元线性回归模型及随机误差、残差、残差分析的概 念. 2.了解最小二乘法的思想方法,会求经验回归方程,并用回归 方程进行预报. 3.会用残差分析判断经验回归模型的拟合效果. 4.了解非线性模型通过变换转化为线性回归模型的思想. 素养·目标定位
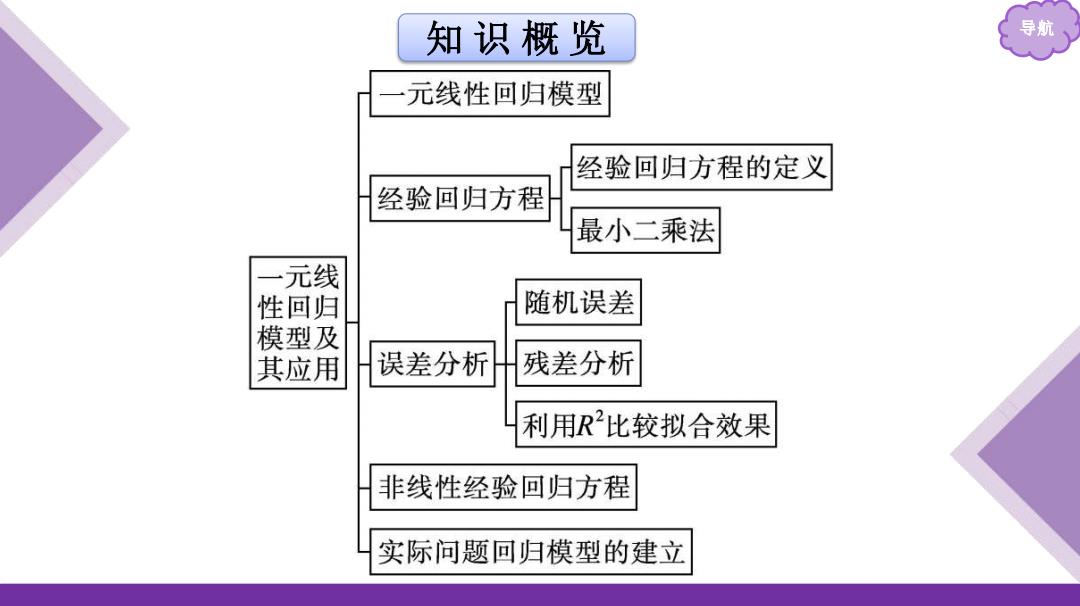
知识概览 导航 元线性回归模型 经验回归方程的定义 经验回归方程 最小二乘法 一元线 性回归 随机误差 模型及 其应用 误差分析 残差分析 利用R比较拟合效果 非线性经验回归方程 实际问题回归模型的建立
知 识 概 览 导航

导期 课前·基础认知 1.一元线性回归模型 用x表示父亲身高,表示儿子身高,表示随机误差假定随机 误差的均值为0,方差为与父亲身高无关的定值σ2,则它们之 (Y=bx+a+e, 间的关系可以表示为Ee)=O.De)二o2,我们称此式为y关于 x的 .其中,称为 或 x称为 或 ;a和b为模型的未 知参数,称为截距参数,b称为斜率参数;e是Y与bx+a之间的
导航 1.一元线性回归模型 用x表示父亲身高,Y表示儿子身高,e表示随机误差.假定随机 误差e的均值为0,方差为与父亲身高无关的定值σ 2 ,则它们之 间的关系可以表示为 𝒀 = 𝒃𝒙 + 𝒂 + 𝒆, 𝑬(𝒆) = 𝟎,𝑫(𝒆) = 𝝈 𝟐 . 我们称此式为 Y 关于 x的 一元线性回归模型 .其中,Y称为 因变量 或 响应 变量 ,x称为 自变量 或 解释变量 ;a和b为模型的未 知参数,a称为截距参数,b称为斜率参数;e是Y与bx+a之间的 随机误差 . 课前·基础认知