R122 i(0)=12A=i(0) uc(0_)=24V=uc(0+) 2.画出=0,等效电路: 电感用电流源替代,电 48V 容用电压源替代。 48-2 R122 ic(0)= 3 _=8A u(0+)=48-2×12=24V R i0)=iz(0+)+ic(0+) 12A 3 48V =12+8=20A t=0,时刻的等效电路 11
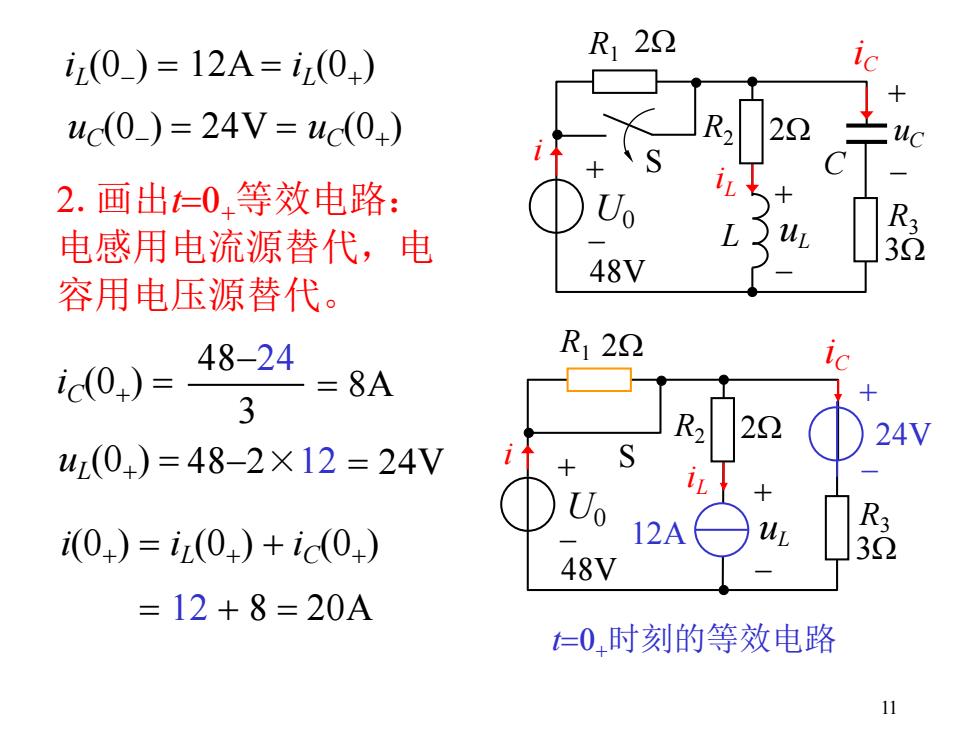
11 2.画出t=0+等效电路: 电感用电流源替代,电 容用电压源替代。 iC(0+ ) = 48-24 3 = 8A uL (0+ ) = 48-2×12 = 24V R1 + - U0 S R2 iL iC 12A + - uL + - R3 3W 2W 2W 48V 24V i R1 + - U0 S R2 iL iC C L + - uL + - uC R3 3W 2W 2W 48V i iL (0- ) = 12A = iL (0+ ) uC(0- ) = 24V = uC(0+ ) i(0+ ) = iL (0+ ) + iC(0+ ) = 12 + 8 = 20A t=0+时刻的等效电路
§7-2一阶电路的零输入响应 >零输入响应:在电源激励为 零的情况下,由动态元件的 (t=0) 初始值(0)引起的响应。 1.RC电路 U 分析RC电路的零输入响应, S 实际上是分析其放电过程。 (t20+) i=- duc duc dt uR=Ri=-RC di 由KVL得: e+uc= RC dt 换路后的“新电路” 阶齐次微分方程 12
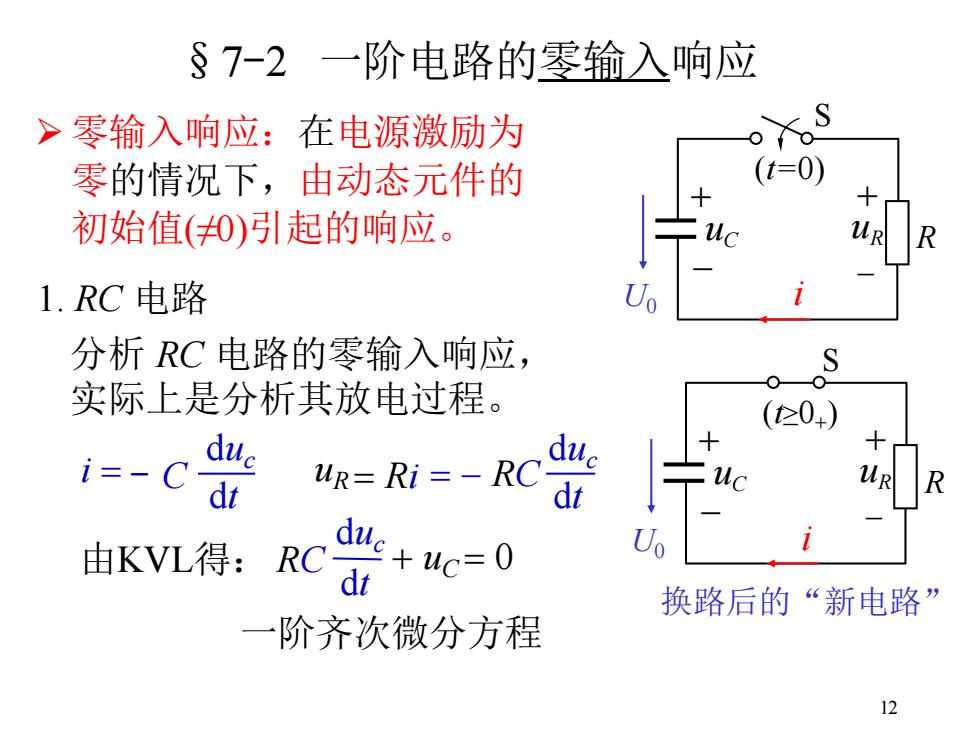
12 §7-2 一阶电路的零输入响应 ➢ 零输入响应:在电源激励为 零的情况下,由动态元件的 初始值(≠0)引起的响应。 1. RC 电路 S R + - uC (t=0) i + - uR U0 S R + - uC (t≥0+ ) i + - uR U0 换路后的“新电路” i = duc dt - C = Ri duc dt = - RC 由KVL得: duc dt RC + uC = 0 uR 分析 RC 电路的零输入响应, 实际上是分析其放电过程。 一阶齐次微分方程
c+uc= S RC dt )特征方程 (t0+) RCp+1=0 特征根P=一之 通解 Ve=Ae Rer U 由初始条件uc(0)=c(0)=U得: =6,c定'=e片,10 t=RC称RC电路的时间常数。 Uo 若R取2,C取F,则为s。 τ的图解 x的大小,反映uc的变化快慢: x越大,uc衰减越慢。 2τ3t 13
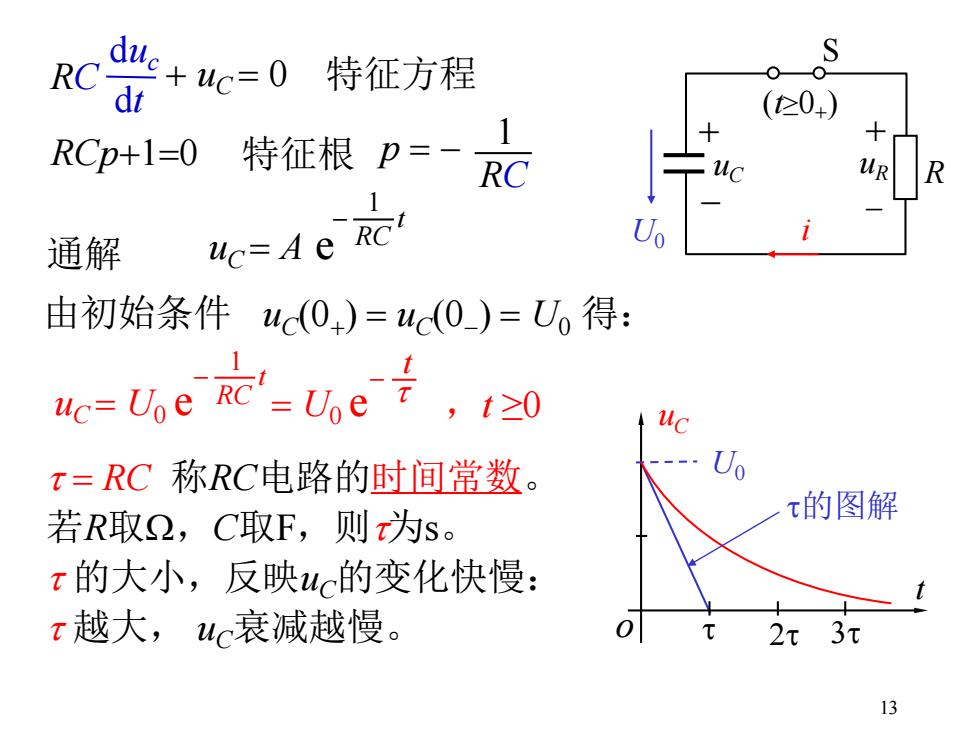
13 t = RC 称RC电路的时间常数。 若R取W,C取F,则t为s。 t 的大小,反映uC的变化快慢: t 越大, uC衰减越慢。 S R + - uC (t≥0+ ) i + - uR U0 p = - RC 1 通解 uC = A e 1 RC - t 由初始条件 uC(0+ ) = uC(0- ) = U0 得: uC = U0 e = U0 e t - 1 t RC - t ,t ≥0 t o uC t 2t 3t U0 t的图解 duc dt RC + uC = 0 特征方程 RCp+1=0 特征根
S 1uc,UR (t20+) ue-le 0.368U 0.05U 在理论上,要经过无 限长时间,uc才能 i=-C U t e dt 衰减到0。 R ·在工程上,认为经过 2(t)Rdt 3x~5x时间,过渡 过程即告结束。 uR=uc=Uoe-t C储存的能量全被R吸收, 并转换成热能消耗掉
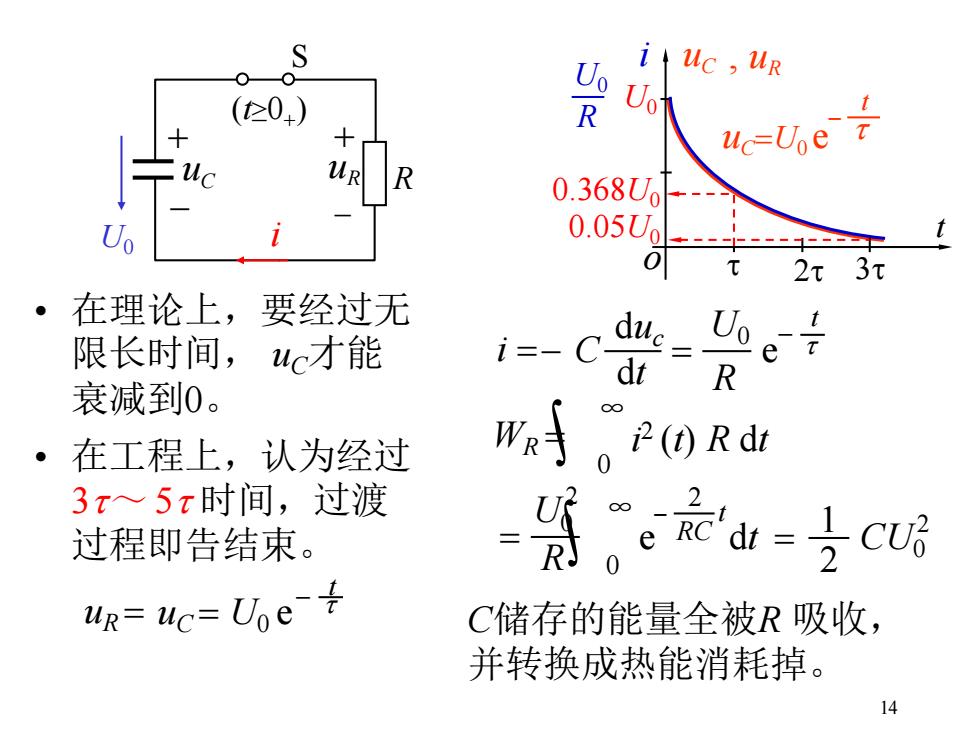
14 t=0,uC =U0 t=t,uC =U0 e -1≈0.638U0 • 在理论上,要经过无 限长时间, uC才能 衰减到0。 • 在工程上,认为经过 3t~ 5t 时间,过渡 过程即告结束。 t o uC t 2t 3t U0 0.368U0 0.05U0 uC=U0 e t - t t=3t,uC =U0 e -3≈0.05U0 t=5t,uC =U0 e -5≈0.007U0 uR = uC = U0 e t - t S R + - uC (t≥0+ ) i + - uR U0 , uR i = duc dt - C = R U0 t - t e WR = ∞ 0 i 2 (t) R dt = ∞ R 0 U0 2 2 RC - t e dt = 2 1 CU0 2 C储存的能量全被R 吸收, 并转换成热能消耗掉。 R U0 i
例:试求仑0时的() R 解: R 4c(0)=10×4 (t( R> 2+4+4 =4V 10V 1F 42 根据换路定则: uc(0)=uc(0+)=4V 换路后,C通过(R∥R2)放电, 42 S20 RegR1∥R2=22o R2 所以T=RgC=2s 1F 42 引用典型电路结果: t 1 uc uc=uc(0.)e T=4e-0.5 V i= =-e0.51A (仑0) (仑0) 15
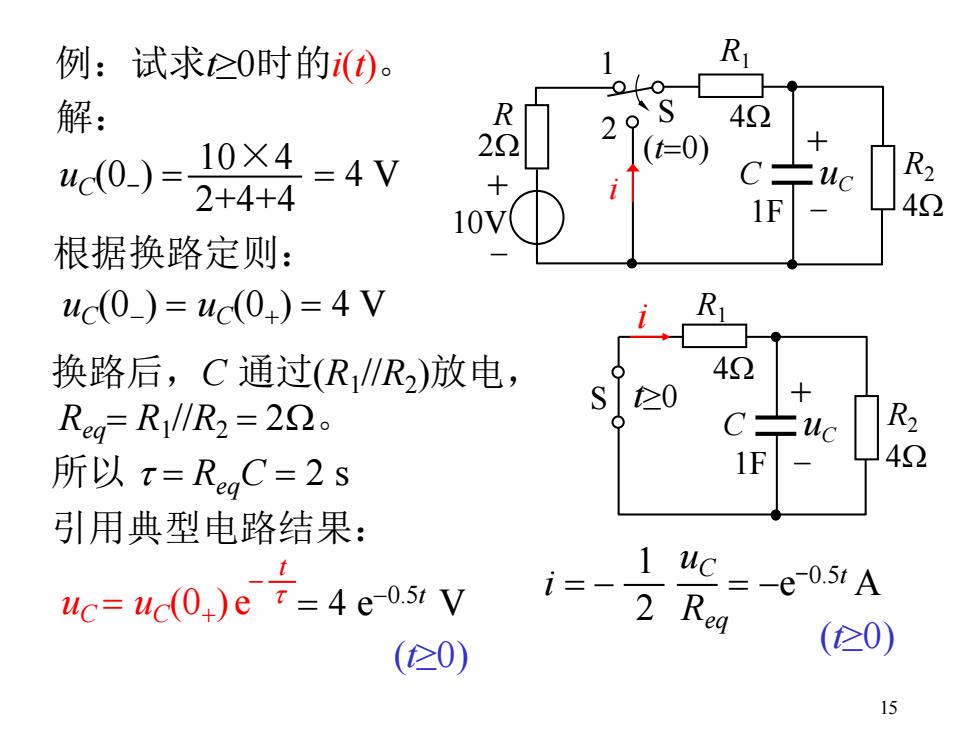
15 例:试求t≥0时的i(t)。 换路后,C 通过(R1 //R2 )放电, Req = R1 //R2 = 2W。 所以 t = ReqC = 2 s 引用典型电路结果: uC(0- ) = 2+4+4 10×4 = 4 V 根据换路定则: uC(0- ) = uC(0+ ) = 4 V R2 + - uC 4W 4W C 1F i S t≥0 R1 uC = uC(0+ ) e t - t = 4 e-0.5t V i = - 2 1 Req uC = -e -0.5t A 解: (t≥0) (t≥0) 2W S R2 + - (t=0) + - uC 4W R1 4W C 1F 1 2 R 10V i