
电路A教案 第三章电阻电路的分析方法 第三章电阻电路的分析方法 教学基本要求: 电路的一般分析是指方程分析法,是以电路元件的约束特性(VC)和电路的托 补约束特性(KCL、KVL)为依据,建立以支路电流或回路电流或结点电压为变量的 电路方程组,解出所求的电压、电流和功率。方程分析法的特点是:(1)具有普遍适 用性,即无论线性和非线性电路都适用:(2)具有系统性,表现在不改变电路结构, 应用KCL,KVL,元件的VCR建立电路变量方程,方程的建立有一套固定不变的步 骤和格式,便于编程和用计算机计算。 本章学习的内容有:电路的图,KCL和KVL的独立方程数。以基尔霍夫定律 为基础,介绍的支路电流法、回路电流法和节点电压法适用于所有线性电路问题的分 析,在后面章节中都要用到。 本章的重点:会用观察电路的方法,熟练应用支路电流法,回路电流法,结点 电压法的“方程通式”写出支路电流方程、回路电流方程、结点电压方程,并求解。 难点: 1.独立回路的确定 2.正确理解每一种方法的依据 3.含独立电流源和受控电流源的电路的回路电流方程的列写 4.含独立电压源和受控电压源的电路的结点电压方程的列写 $3一1电路的图 一、网络图论 图论是拓扑学的一个分支,是富有趣味和应用极为广泛的一门学科。图论的概念 由瑞士数学家欧拉最早提出,欧拉在1736年发表的论文《依据几何位置的解题方法》 中应用图的方法讨论了各尼斯堡七桥难题,见图a和b所示。 图a哥尼斯堡七桥 b对应的图 第1页共16页
电路 A 教案 第三章 电阻电路的分析方法 第 1 页 共 16 页 教学基本要求: 电路的一般分析是指方程分析法,是以电路元件的约束特性(VCR)和电路的拓 补约束特性(KCL、KVL)为依据,建立以支路电流或回路电流或结点电压为变量的 电路方程组,解出所求的电压、电流和功率。方程分析法的特点是:(1)具有普遍适 用性,即无论线性和非线性电路都适用;(2)具有系统性,表现在不改变电路结构, 应用 KCL,KVL,元件的 VCR 建立电路变量方程,方程的建立有一套固定不变的步 骤和格式,便于编程和用计算机计算。 本章学习的内容有:电路的图,KCL 和 KVL 的独立方程数。以基尔霍夫定律 为基础,介绍的支路电流法、回路电流法和节点电压法适用于所有线性电路问题的分 析,在后面章节中都要用到。 本章的重点:会用观察电路的方法,熟练应用支路电流法,回路电流法,结点 电压法的“方程通式”写出支路电流方程、回路电流方程、结点电压方程,并求解。 难点: 1. 独立回路的确定 2. 正确理解每一种方法的依据 3. 含独立电流源和受控电流源的电路的回路电流方程的列写 4. 含独立电压源和受控电压源的电路的结点电压方程的列写 §3-1 电路的图 一、网络图论 图论是拓扑学的一个分支,是富有趣味和应用极为广泛的一门学科。图论的概念 由瑞士数学家欧拉最早提出,欧拉在 1736 年发表的论文《依据几何位置的解题方法》 中应用图的方法讨论了各尼斯堡七桥难题,见图 a 和 b 所示。 图 a 哥尼斯堡七桥 b 对应的图
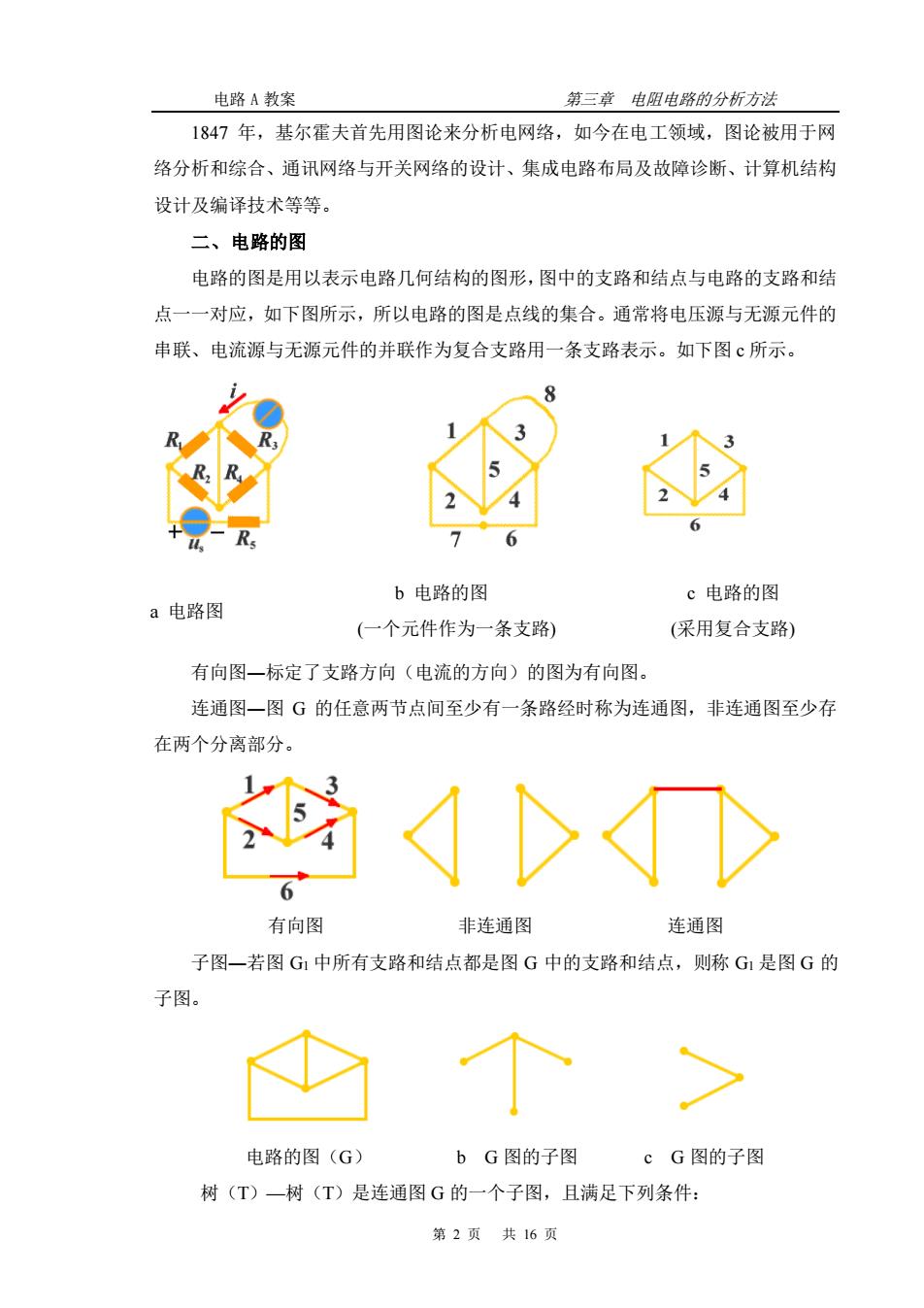
电路A教案 第三章电阻电路的分析方法 1847年,基尔霍夫首先用图论来分析电网络,如今在电工领域,图论被用于网 络分析和综合、通讯网络与开关网络的设计、集成电路布局及故障诊断、计算机结构 设计及编译技术等等。 二、电路的图 电路的图是用以表示电路几何结构的图形,图中的支路和结点与电路的支路和结 点一一对应,如下图所示,所以电路的图是点线的集合。通常将电压源与无源元件的 串联、电流源与无源元件的并联作为复合支路用一条支路表示。如下图c所示。 b电路的图 c电路的图 a电路图 (一个元件作为一条支路) (采用复合支路) 有向图一标定了支路方向(电流的方向)的图为有向图 连通图一图G的任意两节点间至少有一条路经时称为连通图,非连通图至少存 在两个分离部分。 有向图 非连通图 连通图 子图一若图G1中所有支路和结点都是图G中的支路和结点,则称G是图G的 > 电路的图(G) bG图的子图cG图的子图 树(T)一树(T)是连通图G的一个子图,且满足下列条件: 第2页共16页
电路 A 教案 第三章 电阻电路的分析方法 第 2 页 共 16 页 1847 年,基尔霍夫首先用图论来分析电网络,如今在电工领域,图论被用于网 络分析和综合、通讯网络与开关网络的设计、集成电路布局及故障诊断、计算机结构 设计及编译技术等等。 二、电路的图 电路的图是用以表示电路几何结构的图形,图中的支路和结点与电路的支路和结 点一一对应,如下图所示,所以电路的图是点线的集合。通常将电压源与无源元件的 串联、电流源与无源元件的并联作为复合支路用一条支路表示。如下图 c 所示。 a 电路图 b 电路的图 (一个元件作为一条支路) c 电路的图 (采用复合支路) 有向图―标定了支路方向(电流的方向)的图为有向图。 连通图―图 G 的任意两节点间至少有一条路经时称为连通图,非连通图至少存 在两个分离部分。 有向图 非连通图 连通图 子图―若图 G1 中所有支路和结点都是图 G 中的支路和结点,则称 G1 是图 G 的 子图。 电路的图(G) b G 图的子图 c G 图的子图 树(T)—树(T)是连通图 G 的一个子图,且满足下列条件:
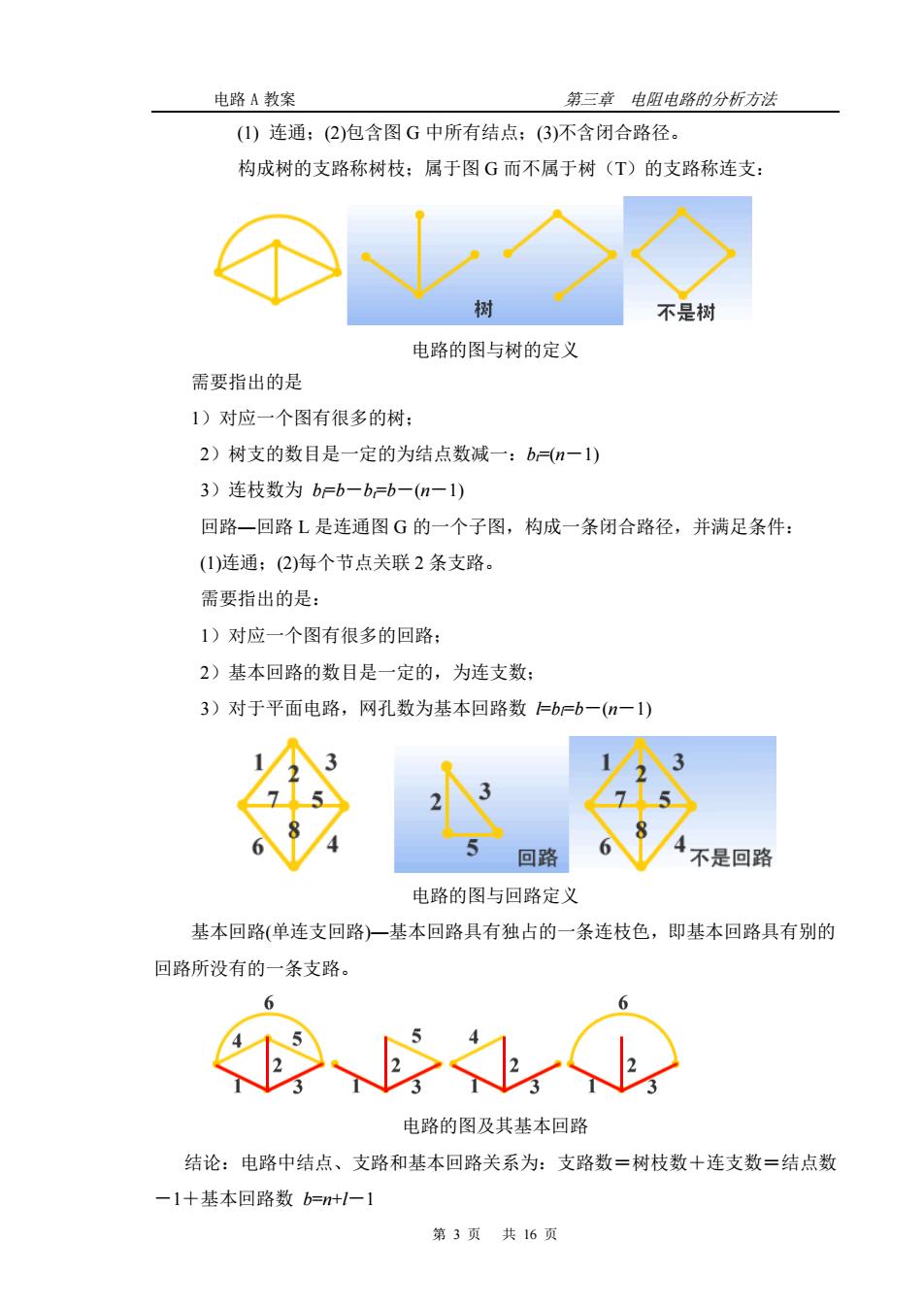
电路A教案 第三章电阻电路的分析方法 (1)连通:(2)包含图G中所有结点:(3)不含闭合路径。 构成树的支路称树枝:属于图G而不属于树(T)的支路称连支: 不是树 电路的图与树的定义 需要指出的是 1)对应一个图有很多的树: 2)树支的数目是一定的为结点数诚一:b(n一1) 3)连枝数为bFb-b=b-(n-1) 回路一回路L是连通图G的一个子图,构成一条闭合路径,并满足条件: (1)连通:(2)海个节点关联2条支路 需要指出的是: 1)对应一个图有很多的回路: 2)基本回路的数目是一定的,为连支数: 3)对于平面电路,网孔数为基本回路数=b=b一(一1) ® 不是回路 电路的图与回路定义 基本回路(单连支回路)一基本回路具有独占的一条连枝色,即基本回路具有别的 回路所没有的一条支路。 电路的图及其基本回路 结论:电路中结点、支路和基本回路关系为:支路数=树枝数十连支数=结点数 一1十基本回路数b=+1-1 第3页共16页
电路 A 教案 第三章 电阻电路的分析方法 第 3 页 共 16 页 (1) 连通;(2)包含图 G 中所有结点;(3)不含闭合路径。 构成树的支路称树枝;属于图 G 而不属于树(T)的支路称连支: 电路的图与树的定义 需要指出的是 1)对应一个图有很多的树; 2)树支的数目是一定的为结点数减一:bt=(n-1) 3)连枝数为 bl=b-bt=b-(n-1) 回路―回路 L 是连通图 G 的一个子图,构成一条闭合路径,并满足条件: (1)连通;(2)每个节点关联 2 条支路。 需要指出的是: 1)对应一个图有很多的回路; 2)基本回路的数目是一定的,为连支数; 3)对于平面电路,网孔数为基本回路数 l=bl=b-(n-1) 电路的图与回路定义 基本回路(单连支回路)―基本回路具有独占的一条连枝色,即基本回路具有别的 回路所没有的一条支路。 电路的图及其基本回路 结论:电路中结点、支路和基本回路关系为:支路数=树枝数+连支数=结点数 -1+基本回路数 b=n+l-1

电路A教案 第三章电阻电路的分析方法 S3-2KCL和KVL的独立方程数 一、KCL的独立方程数 对图中所示电路的图列出4个结点上的KCL方 程(设流出结点的电流为正,流入为负): 结点0-i-。=0 结点②-+坊=0 结点③名++=0 结点④-名+-名=0 把以上4个方程相加,满足:①+②+③十④=0 结论:n个结点的电路,独立的KCL方程为m-1个,即求解电路问题时,只需选 取n-1个结点来列出KCL方程。 二、KVL的独立方程数 根据基本回路的概念,可以证明KVL的独立方程数=基本回路数=b一(n一1)。 结论:n个结点、b条支路的电路,独立的KCL和KVL方程数为:(n一1)+b -(n-1=b $3一3支路电流法 一、支路电流法 以各支路电流为未知量列写独立电路方程分析电路的方法称为支路电流法。 对于有n个节点、b条支路的电路,要求解支路电流,未知量共有b个。只要列 出b个独立的电路方程,便可以求解这b个变量。 二、支路电流方程的列写步骤 1.标定各支路电流(电压)的参考方向: 2.从电路的n个结点中任意选择n一1个结点列写KCL方程: 3.选择基本回路,结合元件的特性方程列写b一(一I)个KVL方程: 4.求解上述方程,得到b个支路电流: 5.进一步计算支路电压和进行其它分析。 需要注意的是 第4页共16页
电路 A 教案 第三章 电阻电路的分析方法 第 4 页 共 16 页 §3-2 KCL 和 KVL 的独立方程数 一、KCL 的独立方程数 对图中所示电路的图列出 4 个结点上的 KCL 方 程(设流出结点的电流为正,流入为负): 结点① 结点② 结点③ 结点④ 把以上 4 个方程相加,满足:①+②+③+④=0 结论:n 个结点的电路, 独立的 KCL 方程为 n-1 个,即求解电路问题时,只需选 取 n-1 个结点来列出 KCL 方程。 二、KVL 的独立方程数 根据基本回路的概念,可以证明 KVL 的独立方程数=基本回路数=b-(n-1)。 结论:n 个结点、b 条支路的电路, 独立的 KCL 和 KVL 方程数为:(n-1)+ b -(n-1)=b §3-3 支路电流法 一、支路电流法 以各支路电流为未知量列写独立电路方程分析电路的方法称为支路电流法。 对于有 n 个节点、b 条支路的电路,要求解支路电流,未知量共有 b 个。只要列 出 b 个独立的电路方程,便可以求解这 b 个变量。 二、支路电流方程的列写步骤 1. 标定各支路电流(电压)的参考方向; 2. 从电路的 n 个结点中任意选择 n-1 个结点列写 KCL 方程; 3. 选择基本回路,结合元件的特性方程列写 b-(n-1)个 KVL 方程; 4. 求解上述方程,得到 b 个支路电流; 5. 进一步计算支路电压和进行其它分析。 需要注意的是

电路A教案 第三章电阻电路的分析方法 支路电流法列写的是KCL和KVL方程,所以方程列写方便、直观,但方程数 较多,宜于利用计算机求解。人工计算时,适用于支路数不多的电路。 三、支路电流方程的应用 例:求图示电路的各支路电流及电压源各自发出的功率。 11 7 70v 6vd② 解:(1)对结点a列KCL方程:-2+5=0 711-1112=70-6 (2)对两个网孔列KVL方程:11I2+7I3=6 (3)求解上述方程: 上1-1 10-11 卜101 △=7-110=203△1=64-110=1218△2=7640=-406 0117 6117 067 4-会6A-会 -406 =h+h=6-2=4 (4)电压源发出的功率: P70=6×70=420W P6=-2×6=-12W 例:列写图示电路的支路电流方程(电路含有理想电流源) 11 70 解法1:(1)对结点a列KCL方程:-h+乃=0 (2)选两个网孔为独立回路,设电流源两端电压为U,列KVL方程: 7l1-11h=70-U 11h+73=U (3)由于多出一个未知量U,需增补一个方程:h=6A 求解以上方程可得各支路电流。 第5页共16页
电路 A 教案 第三章 电阻电路的分析方法 第 5 页 共 16 页 支路电流法列写的是 KCL 和 KVL 方程,所以方程列写方便、直观,但方程数 较多,宜于利用计算机求解。人工计算时,适用于支路数不多的电路。 三、支路电流方程的应用 例:求图示电路的各支路电流及电压源各自发出的功率。 解:(1)对结点 a 列 KCL 方程: -I1-I2+I3=0 (2)对两个网孔列 KVL 方程: (3)求解上述方程: I3=I1+I2=6-2=4 (4)电压源发出的功率: P70=6×70=420W P6=-2×6=-12W 例:列写图示电路的支路电流方程(电路含有理想电流源) 解法 1:(1)对结点 a 列 KCL 方程: -I1-I2+I3=0 (2)选两个网孔为独立回路,设电流源两端电压为 U ,列 KVL 方程: 7I1-11I2=70-U 11I2+7I3=U (3)由于多出一个未知量 U,需增补一个方程: I2=6A 求解以上方程可得各支路电流