
离散数学 无向哈密顿图的一个必要条件 定理13.2设无向图G=<V,E>是哈密顿图,对于任意VcV且 V≠O,均有p(G-V)≤V 证设C为G中一条哈密顿回路 (1)p(C-V)≤IVW (2)p(G-V)≤p(C-V1)≤IV (因为C=G) 推论设无向图G=<V,E>是半哈密顿图,对于任意的VcV 且V≠⑦均有 p(G-V)≤IV+1 证设为从到v的哈密顿通路,令G=GU(w,),则G为 哈密顿图.于是 p(G-Vi)=p(G'-V1-(w)≤p(G'-V)+1≤IVi+1 11
11 无向哈密顿图的一个必要条件 定理13.2 设无向图G=<V,E>是哈密顿图,对于任意V1V且 V1,均有p(G−V1 ) |V1 | 证 设C为G中一条哈密顿回路 (1) p(C−V1 ) |V1 | (2) p(G−V1 ) p(C−V1 ) |V1 | (因为CG) 推论 设无向图G=<V,E>是半哈密顿图,对于任意的V1V 且V1均有 p(G−V1 ) |V1 |+1 证 设 为从u到v的哈密顿通路,令G = G(u,v),则G为 哈密顿图. 于是 p(G−V1 ) = p(G−V1−(u,v)) p(G−V1 )+1 |V1 |+1
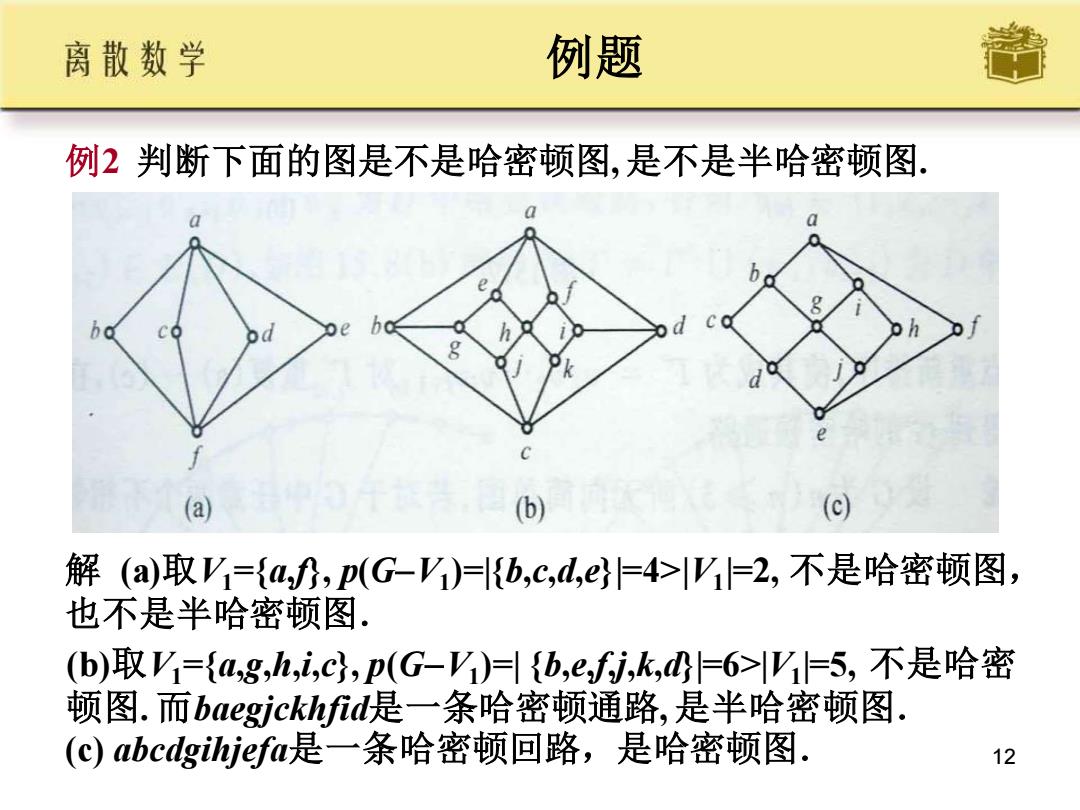
离散数学 例题 例2判断下面的图是不是哈密顿图,是不是半哈密顿图 (a) (b) (c) 解(a)取V={a,,p(G-V)={b,c,,}=4>V1=2,不是哈密顿图, 也不是半哈密顿图. (b)取V={a,g,h,i,c以,p(G-y)={b,e,fi,k,G=6>lY1=5,不是哈密 顿图.而baegjckhfid是一条哈密顿通路,是半哈密顿图. (c)abedgihjefa是一条哈密顿回路,是哈密顿图. 12
12 例题 例2 判断下面的图是不是哈密顿图, 是不是半哈密顿图. 解 (a)取V1={a,f}, p(G−V1 )=|{b,c,d,e}|=4>|V1 |=2, 不是哈密顿图, 也不是半哈密顿图. (b)取V1={a,g,h,i,c}, p(G−V1 )=| {b,e,f,j,k,d}|=6>|V1 |=5, 不是哈密 顿图. 而baegjckhfid是一条哈密顿通路, 是半哈密顿图. (c) abcdgihjefa是一条哈密顿回路,是哈密顿图.

离散数学 例题 例3设G为阶无向连通简单图,若G中有割点或桥,则G不 是哈密顿图. 证设v为割点,则p(G-)≥2>K以=1. K有桥,它显然不是哈密顿图.除K外,其他有桥的连 通图均有割点 13
13 例题 例3 设G为n阶无向连通简单图,若G中有割点或桥,则G不 是哈密顿图. 证 设v为割点,则p(G−v) 2>|{v}|=1. K2有桥,它显然不是哈密顿图. 除K2外,其他有桥的连 通图均有割点

离散数学 无向哈密顿图的一个充分条件 定理13.3设G是阶无向简单图,若对于任意不相邻的顶点 ,均有 d(y)+d(y)≥n-1 (*) 则G中存在哈密顿通路. 推论设G为n(n≥3)阶无向简单图,若对于G中任意两个不相 邻的顶点,均有 d(y+dy)≥n (**) 则G中存在哈密顿回路 14
14 无向哈密顿图的一个充分条件 定理13.3 设G是n阶无向简单图, 若对于任意不相邻的顶点 vi ,vj , 均有 d(vi )+d(vj ) n−1 () 则G 中存在哈密顿通路. 推论 设G为n (n3) 阶无向简单图, 若对于G中任意两个不相 邻的顶点vi ,vj , 均有 d(vi )+d(vj ) n () 则G中存在哈密顿回路

离散数学 判断是否为哈密顿图 判断是否为(半)哈密顿图至今还是一个难题. ()观察出一条哈密顿回路或哈密顿通路。 (2)证明满足充分条件. (3)证明不满足必要条件. 例4证明右图(周游世界问题)是哈密顿图 abcdefghijkImnopqrsta 是一条哈密顿回路 注意,此图不满足定理11.3推论的条件. 例5完全图Kn(≥3)是哈密顿图. 证任何两个项点u,y,d(w+d(y)=2(n-1)≥n 15
15 判断是否为哈密顿图 判断是否为(半)哈密顿图至今还是一个难题. (1) 观察出一条哈密顿回路或哈密顿通路. (2) 证明满足充分条件. (3) 证明不满足必要条件. 例4 证明右图(周游世界问题)是哈密顿图 证 a b c d e f g h i j k l m n o p q r s t a 是一条哈密顿回路. 注意,此图不满足定理11.3推论的条件. 例5 完全图Kn (n3)是哈密顿图. 证 任何两个顶点u,v,d(u)+d(v) = 2(n−1) n