
离散数学 Fleury算法 算法: (1)任取y∈(G),令Po=y,=0. (2)设P:=oe1y1e2.eyi, 如果E(G)-{e1,e2,,e}中没有与y关联的边,则计算结束; 否则按下面方法从E(G)-{e1,e2,,e}中选取e+1: (a)e1与y,关联; (b)除非无别的边可供选择,否则e+1不应为G-{e1,e2,e 中的桥. 设e#1=(y%y+1),把e1y+1加入P (3)令=计1,返回(2). 6
6 Fleury算法 算法: (1) 任取v0V(G), 令P0=v0 , i=0. (2) 设Pi = v0e1v1e2…eivi , 如果E(G)-{e1 ,e2 ,…,ei }中没有与vi关联的边, 则计算结束; 否则按下面方法从E(G)−{e1 ,e2 ,…,ei }中选取ei+1: (a) ei+1与vi 关联; (b) 除非无别的边可供选择, 否则ei+1不应为 G−{e1 ,e2 ,…,ei } 中的桥. 设ei+1=(vi ,vi+1), 把ei+1vi+1加入Pi . (3) 令i=i+1, 返回(2)
离散数学 实例 一笔画出一条欧拉回路 7
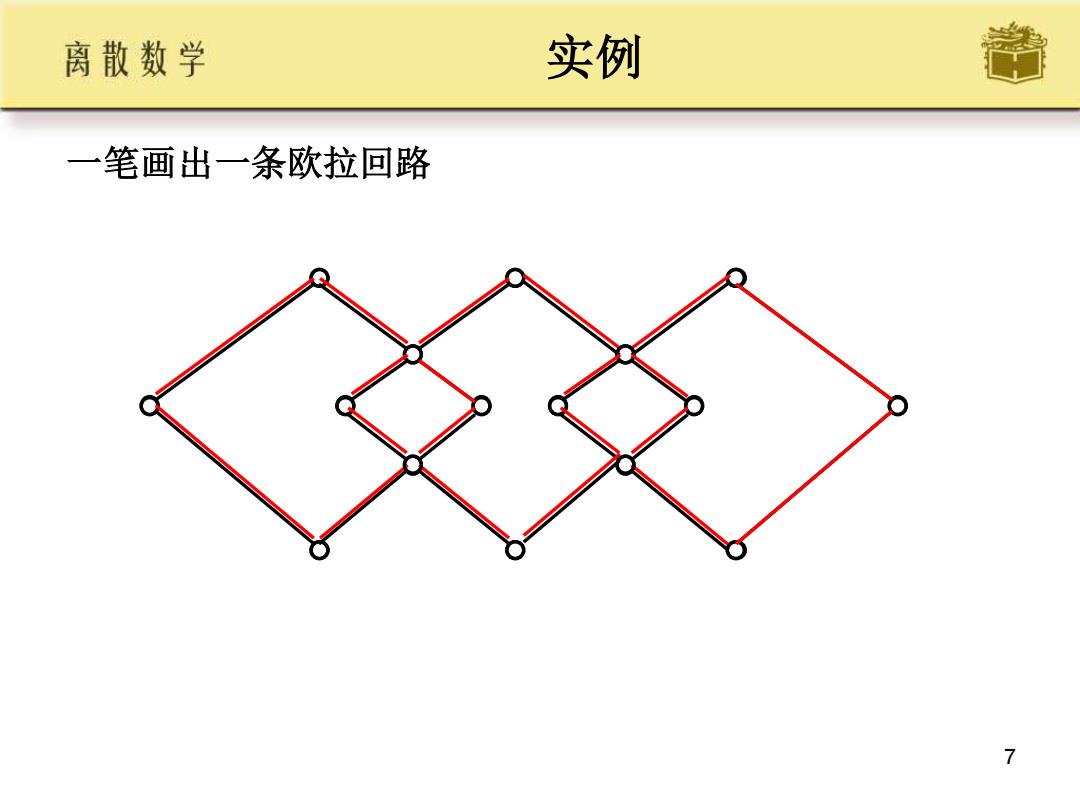
7 实例 一笔画出一条欧拉回路
离散数学 实例 一笔画出一条欧拉回路 8
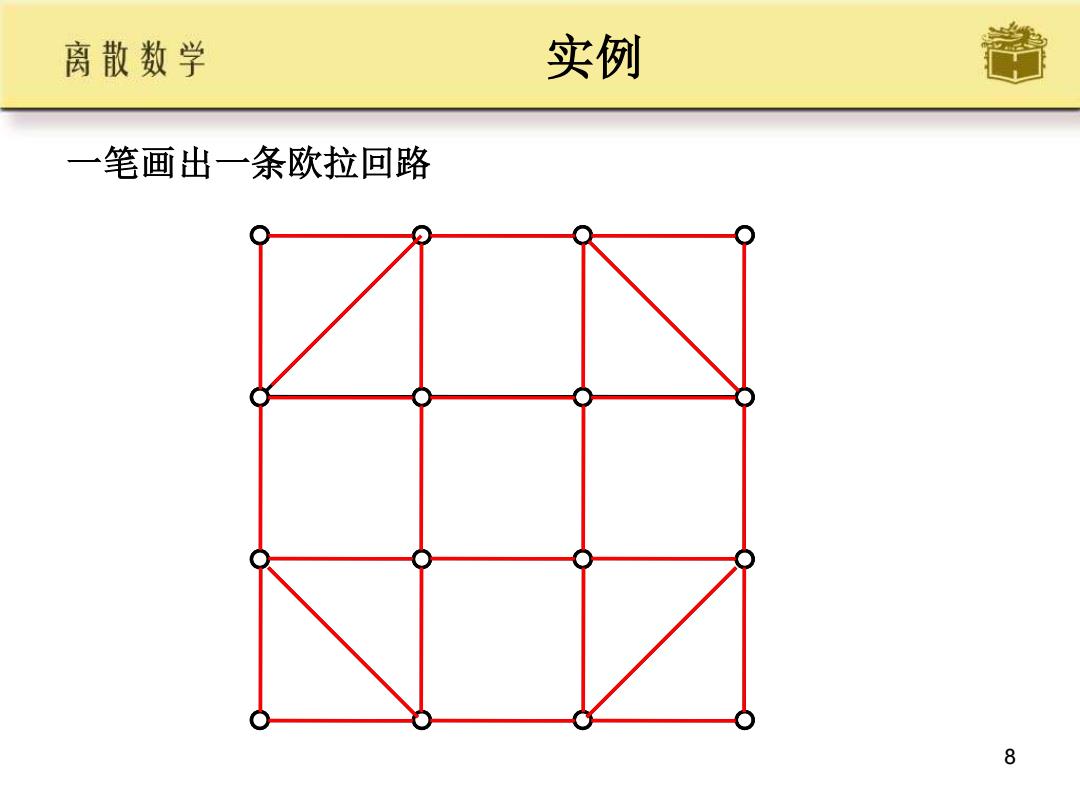
8 实例 一笔画出一条欧拉回路
离散数学 13.2哈密顿图 历史背景:哈密顿周游世界问题 (1) (2) 9
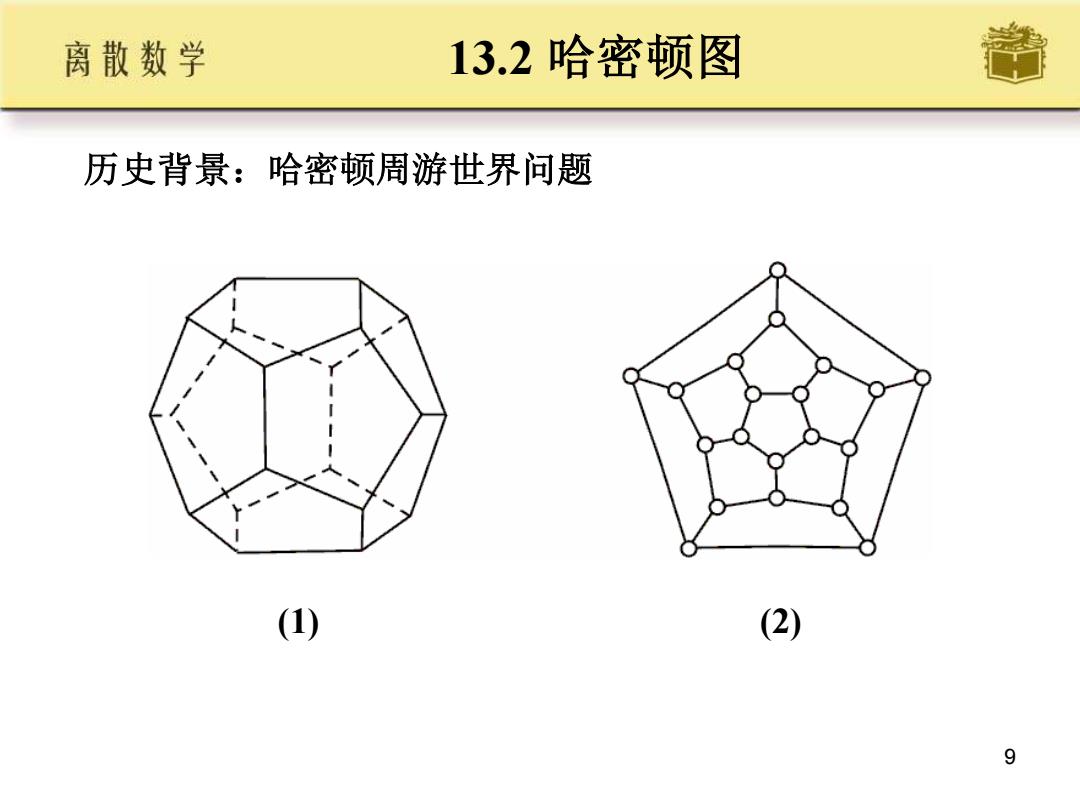
9 13.2 哈密顿图 历史背景:哈密顿周游世界问题 (1) (2)
离散数学 哈密图与半哈密顿图 定义13.2经过图中所有顶点一次且仅一次的通路称作哈密顿 通路.经过图中所有顶点一次且仅一次的回路称作哈密顿回 路.具有哈密顿回路的图称作哈密顿图.具有哈密顿通路且无 哈密顿回路的图称作半哈密顿图. 规定:平凡图是哈密顿图 例 哈密顿图 哈密顿图 半哈密顿图 不是 10
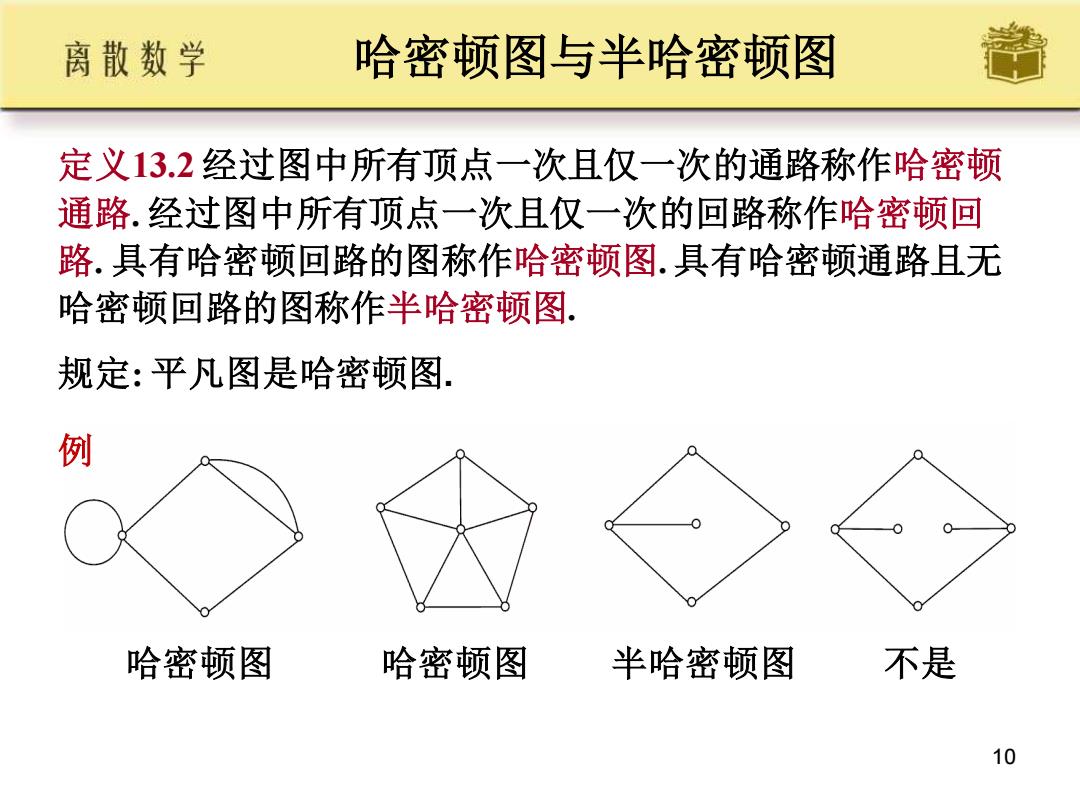
10 哈密顿图与半哈密顿图 定义13.2 经过图中所有顶点一次且仅一次的通路称作哈密顿 通路. 经过图中所有顶点一次且仅一次的回路称作哈密顿回 路. 具有哈密顿回路的图称作哈密顿图. 具有哈密顿通路且无 哈密顿回路的图称作半哈密顿图. 规定: 平凡图是哈密顿图. 哈密顿图 哈密顿图 半哈密顿图 例 不是