
第五章函数 函数也叫映射,交换,是数学中的一个基本概念 在高数中,函数的概念是从变量的角度提出来的 这种函数一般是连续或间断连续的函数,这里将 连续函数的概念推广到离散量的讨论,即将函数 看作一种特殊的二元关系。 173
1/73 第五章 函数 函数也叫映射,交换,是数学中的一个基本概念, 在高数中,函数的概念是从变量的角度提出来的, 这种函数一般是连续或间断连续的函数,这里将 连续函数的概念推广到离散量的讨论,即将函数 看作一种特殊的二元关系

5.1函数的基本概念 定义5.,1:设f是集合A到B的关系,如果对每个x∈ A,都存在唯,一y∈B,,使得<X,y>Ef,则称关系f 为A到B的函数(Funct ion),记为f:A+B。当<x, y)∈f时,正常记为y=f(x),x称为自变量,y为x 在f下的函数值。 ()domf=A,称为函数的定义域; (2)ran fCB,称为函数的值域,ranf也可记为 f(A),为A在f下的像; (3)<x,y>∈f∧<x,2>∈f→y=2; (4)|fl=|A; (5)f(x)仅表示一个变值,f表示一个集合,. f≠f(x) 2/73
2/73 5.1 函数的基本概念 • 定义5.1:设f是集合A到B的关系,如果对每个x A,都存在唯一y B,使得<x,y> f,则称关系f 为A到B的函数(Function),记为f:A→B。当<x, y> f时,正常记为y=f(x),x称为自变量,y为x 在f下的函数值。 (1)dom f=A,称为函数的定义域; (2)ran f B,称为函数的值域,ran f也可记为 f(A),为A在f下的像; (3) ; (4)|f|=|A|; (5)f(x)仅表示一个变值,f表示一个集合, ∴ x, y f x,z f y = z f f (x)
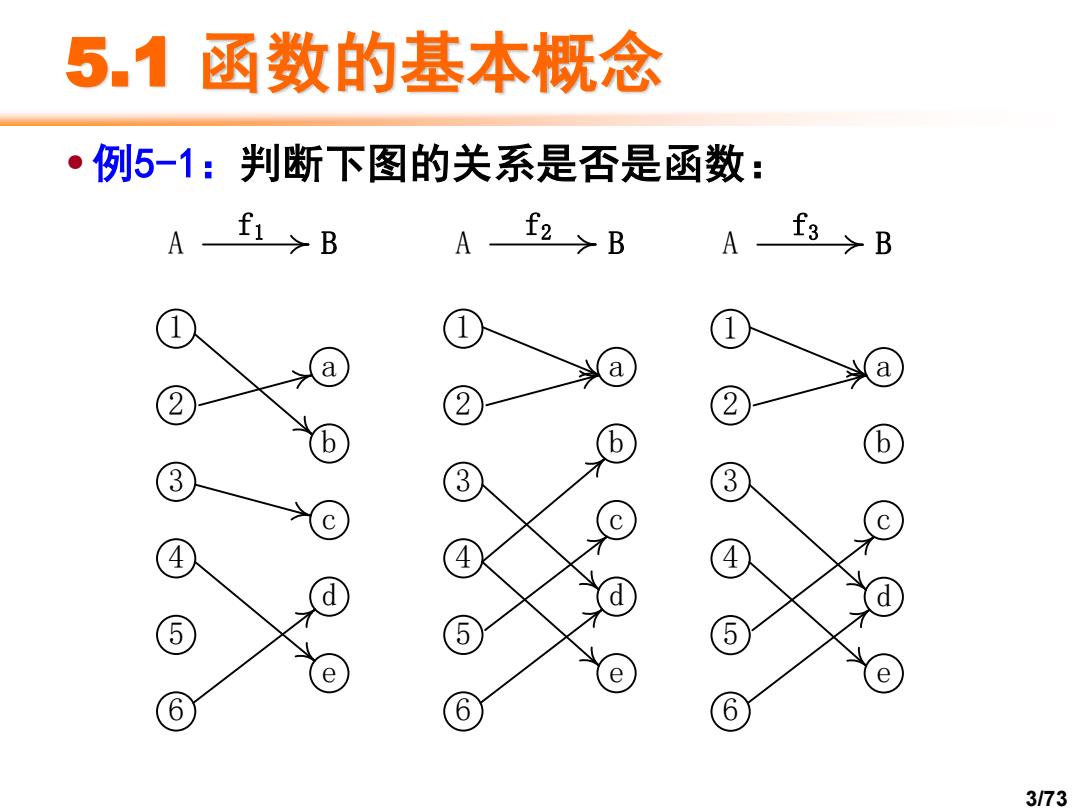
5.1函数的基本概念 例5-1:判断下图的关系是否是函数: A f1B A f2>B A a 2 3 5 e e 6 6 6 3/73
3/73 5.1 函数的基本概念 •例5-1:判断下图的关系是否是函数: 1 2 3 4 5 6 a b c d e A B f1 1 2 3 4 5 6 a b c d e A B f2 1 2 3 4 5 6 a b c d e A B f3

5.1函数的基本概念 例5-2:设A={a,b},B={1,2},则AXB={Ka,1>, <a,2>,<b,1>,<b,2>},此时A到B的不同关系有 16个;A到B的不同的函数有4个; f={<a,1>,<b,1>},f3={<a,1>,<b,2>}, f3={<a,2>,<b,1>},f4={<a,2>,<b,2>} ()AB的任何一个子集,都是A到B的关系,因此 从A到B的不同的关系有241个,但从A到B的不 同的函数却只有1BM个; ·(2)每个函数的基数为|A,但关系的基数可以为0 一直到AX B; 。(3)每个函数的第一个元素一定互不相同; ·(4)将A到B的一切函数构成的集合记为B={fIf:A→B; 4/73
4/73 5.1 函数的基本概念 •例5-2:设A={a,b},B={1,2},则A×B={<a,1>, <a,2>,<b,1>,<b,2>},此时A到B的不同关系有 16个;A到B的不同的函数有4个; • (1)A×B的任何一个子集,都是A到B的关系,因此 ,从A到B的不同的关系有 个,但从A到B的不 同的函数却只有 个; • (2)每个函数的基数为|A|,但关系的基数可以为0 一直到|A|×|B|; • (3)每个函数的第一个元素一定互不相同; • (4)将A到B的一切函数构成的集合记为 { ,2 , ,1 }, { ,2 , ,2 }. { ,1 , ,1 }, { ,1 , ,2 }, 3 4 1 2 = = = = f a b f a b f a b f a b | | | | 2 A B | | | | A B B { f | f : A B} A = →

5.2函数的性质 ·定义5.2:设f是从集合A到B的函数: (1)对x,x2∈A,若x≠x2,则f(x)≠f(x2),则称f为从A 到B的单射(Injection); (2)若ranf=B,则称f为A到B的满射(Sur jection); (3)若f既是单射,又是满射,则称f为从A到B的双射 (Bijection)或一一映射; (4)若A=B,则称f为A上的函数,当A上的函数f是双 射,称f为变换(Transform)。 >(1)f是单射的必要条件为|A≤B|,(2)f为满射 的必要条件为B|≤|A,(3)f为双射的必要条件 为A=B|。 5/73
5/73 5.2 函数的性质 •定义5.2:设f是从集合A到B的函数: (1)对 ,则称f为从A 到B的单射(Injection); (2)若ran f=B,则称f为A到B的满射(Surjection); (3)若f既是单射,又是满射,则称f为从A到B的双射 (Bijection)或一一映射; (4)若A=B,则称f为A上的函数,当A上的函数f是双 射,称f为变换(Transform)。 ➢(1)f是单射的必要条件为|A|≤|B|,(2)f为满射 的必要条件为|B|≤|A|,(3)f为双射的必要条件 为|A|=|B|。 , , , ( ) ( ) 1 2 1 2 1 2 x x A 若x x 则f x f x