
离散数学 第三部分图论 本部分主要内容 图的基本概念 ·树 欧拉图与哈密顿图 二部图与匹配 ● 平面图 着色 1
1 第三部分 图论 本部分主要内容 ⚫ 图的基本概念 ⚫ 树 ⚫ 欧拉图与哈密顿图 ⚫ 二部图与匹配 ⚫ 平面图 ⚫ 着色

离散数学 第十一章图的基本概念 主要内容 ●图 ● 通路与回路 图的连通性 图的矩阵表示 预备知识 ● 多重集合一一元素可以重复出现的集合 ● 无序集一一A&B={cy)川x∈Ay∈B} 2
2 第十一章 图的基本概念 主要内容 ⚫ 图 ⚫ 通路与回路 ⚫ 图的连通性 ⚫ 图的矩阵表示 预备知识 ⚫ 多重集合——元素可以重复出现的集合 ⚫ 无序集——AB={(x,y) | xAyB}
离散数学 11.1图 定义11.1无向图G=<V,E>,其中 ()为非空有穷集,称为顶点集,其元素称为顶点 (2)E为V&V的多重有穷集,称为边集,其元素称为无向边,简 称边 例无向图G=<V,E>,其中 V={y1,2,3,V4,s, E={(1,y1),(y12),(y2,3),((2,3), 0 (2,s),(y1,s),(y4,ys)} A
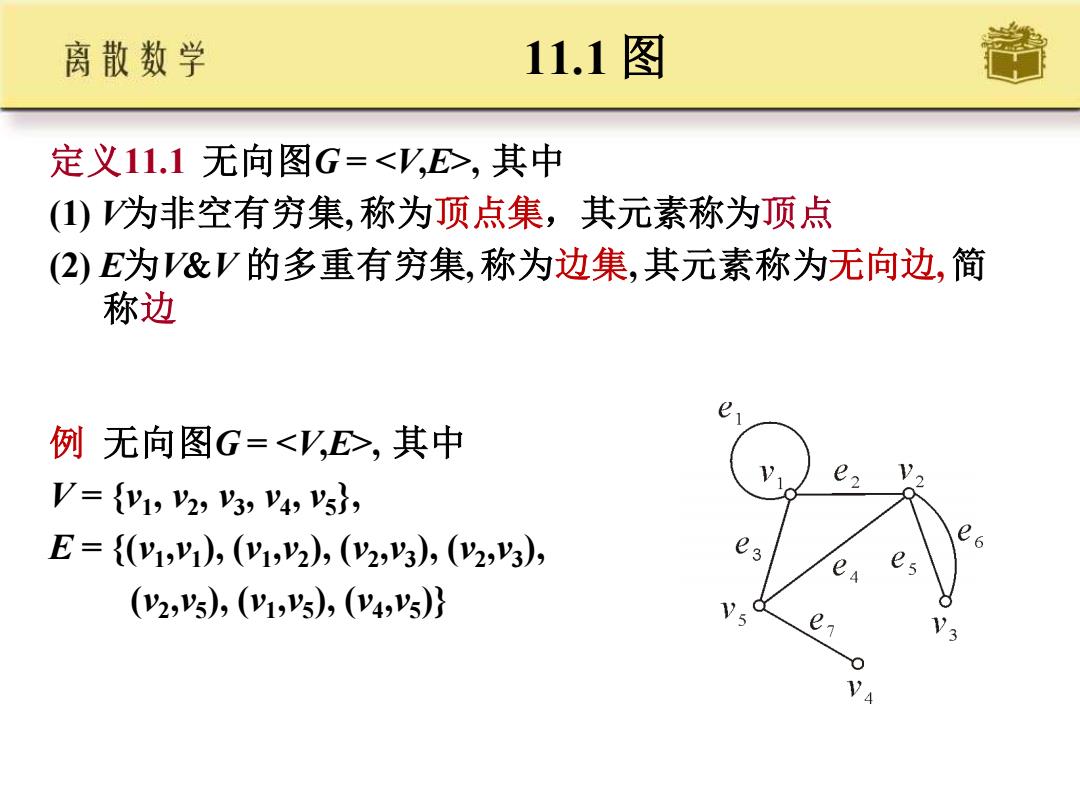
11.1 图 定义11.1 无向图G = <V,E>, 其中 (1) V为非空有穷集, 称为顶点集,其元素称为顶点 (2) E为VV 的多重有穷集, 称为边集, 其元素称为无向边, 简 称边 例 无向图G = <V,E>, 其中 V = {v1 , v2 , v3 , v4 , v5 }, E = {(v1 ,v1 ), (v1 ,v2 ), (v2 ,v3 ), (v2 ,v3 ), (v2 ,v5 ), (v1 ,v5 ), (v4 ,v5 )}

离散数学 有向图 定义11.2有向图D=<V,E>,其中 ()Ψ为非空有穷集,称为顶点集,其元素称为顶点 (2)E为%V的多重有穷集,称为边集,其元素称为有向边,简 称边 例有向图D=<V,E>,其中 b V-fa,b,c,dj E={<a,>,<,b>,<a,b>,<,, 0 <d,c>,<c,b,<c,b>} a 注意:图的集合表示与图形表示之间的对应 4
4 有向图 定义11.2 有向图D=<V,E>,其中 (1) V 为非空有穷集, 称为顶点集,其元素称为顶点 (2) E为VV 的多重有穷集, 称为边集, 其元素称为有向边, 简 称边 例 有向图D=<V,E>, 其中 V={a,b,c,d} E={<a,a>,<a,b>,<a,b>,<a,d>, <d,c>,<c,d>,<c,b>} 注意:图的集合表示与图形表示之间的对应

离散数学 相关概念 1.无向图和有向图通称图.记顶点集(G,边集E(G 2.图的阶,n阶图. 3.n阶零图N,平凡图N, 4.空图0. 5.标定图与非标定图. 6.有向图的基图. 7.无向图中顶点与边的关联及关联次数,顶点与顶点、边与 边的相邻关系. 8.有向图中顶点与边的关联,顶点与顶点、边与边的相邻关 系 9.环,孤立点。 5
5 相关概念 1. 无向图和有向图通称图. 记顶点集V(G), 边集E(G). 2. 图的阶, n阶图. 3. n 阶零图Nn , 平凡图N1 . 4. 空图. 5. 标定图与非标定图. 6. 有向图的基图. 7. 无向图中顶点与边的关联及关联次数, 顶点与顶点、边与 边的相邻关系. 8. 有向图中顶点与边的关联, 顶点与顶点、边与边的相邻关 系. 9. 环, 孤立点