
1374第七篇其他金融机构实务定量分析 期的收入较平稳,承租单位较易接受。但在高科技年代,设 租金清偿期不长,但租金总额也较大,因为在宽缓期间虽然 备更新快,对某些淘汰性很强的设备,本金均衡偿还不尽合没有支付租金,但是已经起息,增加了租赁成本。所以,租金 理,因为设备的有形磨损在使用期间不是均等的。而定率法 清偿期要根据承租人的实际经济状况而定。 可弥补定额法的缺陷。定率法的租用费回收是前期较高,后 期较低,对那些短期内生产能力高,有形磨损和无形磨损较融资利率分析(Financing Interest Rate Analysis)】 强的设备,就应前期多收回,后期少收回,这对承租人与出租 利率是影响租金总额的主要因素之一,一般来说,利率 人负担和影响都不大。于是,对于使用期较长的大型设备来越高,租金总额也随之增加。但是,由于租金计算方法的不 讲,使用前期负担过重也不合理。所以,结合实际租赁情况,同,同样的利率,可能会造成租金总额悬殊,如在同样利率条 选择适当的计算方式。 件下,采用附加率法要比等额年金计算的租金多。租金先付 3.本利均等方式。指承租者支付每期的租用费中,本金 和后付,在同一利率条件下,租金总额也有差别。 和利息均等的方式。或者说,承租者以每期相等的租用费支 除此之外,利息计算方法不同,在同一利率的情况下,对 付出租者的计算方法。它不同于等额年金法。其计算公 租金总额的大小也有重要影响。 式为: 国际上利息计算有三种方法:1.大陆法。是指一年中每 P R.=上+A 个月份的天数都视为30天,对年对月计算,以360/360表示 n 1- (1+r)网 生息天数和基础天数的关系。2.英国法。是以365/365表 式中,R。—每期支付的租用费: 示生息天数和基础天数的关系,逢闰年改为366/365,即把 P一成本: 365天作基础天数,同时严格按照日历计算生息天数。3.欧 n一租期; 洲货币法。是以365/360表示生息天数和基础天数的关系, A一每期支付的定额: 逢闰年改为366/360,即按实际日历天数计算生息天数,基础 一利率。 天数定为360天。 采用大陆法计算利息,由于计息天数和基础天数相同. 例如,某企业向信托机构租用设备,概算成本为100万 元,租期5年,每年支付一次租金,利率为10%。 一般不会对租金产生影响。采用英国法,除闰年有一天的利 因为等额支付本金,所以,100万元/5=20(万元) 息差额外,平年时不会影响租金。欧洲货币法由于生息天数 而利息也等额支付,用资本回收期数求得,而每期支付 与基础天数不同,造成实际利息率提高,使总租金增加。如: 的定额为20万元。 年利率为10%,用欧洲货币法计算实际年利率:(1)以365 天为生息天数的实际年利率为:365/360×10%=10.138 10% 20× =6.31(万元) 1 9%:(2)以366天为生息天数的实际年利率为:10%×366/ 1-1+10%) 360=10.1667%。由此可见,实际年利率在平年时提高了 R.=20+6.31=26.31(万元) 0.1389%.在闰年时提高0.1667%。 采用大陆法计算利息时,要注意每个月都视为30天,尽 信托资金计划(Trust Cash Planning) 管有的月份为31天,也只能按30天计算。 信托资金计划指以资金为主要对象,以年度为基本期, 计息惯例,是以算头不算尾或者算尾不算头为原则。 在计划期内反映资金来源和资金运用的数量和方向,以及两 关于计息方法,在租赁合同中要明确规定,如果合同没 者之间的平衡关系的规划。 有明确计息方法,按惯例,采用合同货币使用国的计算方法。 信托资金计划包括资金来源和资金运用两大部分:资金 参见“利息计算方法对租金总额的影响”条。 米源包括自有资金、信托存款、委托存款、发行股票、债券、当 年结益和其他资金来源:资金运用包括信托贷款、固定资产 租赁费(Lease Rentals) 投资、委托贷款和投资、金融租赁、缴存准备金和其他资金运 租赁费指出租人为承租人采购租赁物件所需的营业费 用等。 用。如办公费、差旅费、邮费、银行费用、工资等。租赁费是 租金重要组成部分。出租人收取租赁费的方法有两种,一种 租金清偿期(Rent Liquidation Period) 是在签订租赁合同时,一次性收取:另一种是计入成本,以租 租金清偿期指融资租赁合同规定的第一笔租金支付日金成本分次收取。对于租赁费的不同计算方法,承租人负担 起,至最后一笔租金支付日止的期间。租金清偿期长,租金是不同的。 总额则大,但每期支付租金相对少些:反之,租金清偿期短, 如果租赁成本为100万元,租期3年,分6次付租,年利 租金总额小些,但每次支付租金相对则高些。租金清偿期与为10%,租赁费率为1.5%,求不同计算法的租费。 租赁期限不同,租赁期限是从起租日算起,到付清最后一期 1.以概算成本为基数,一次收取: 租金为止。这里相差是起租日至支付第一期租金的期间。 1000000×1.5%=15000(元) 它包括租金支付间隔期和租金宽缓期,如果这段期间较长, 2.以租金总额为基数,一次收取:

第2章金融信托租赁业务1375 租金总额:∑R=197017×6=1182102(元) 式中,R一每期租金: 租赁费:1182102×1.5%=17732(元) P一概算成本: 可见,第二种计算法比第一种增加2732元。 n—租期(次数): 3.纳人概算成本计算,计入租金。 —每期利率: 加人成本=1000000×(1+1.5%)=1015000(元) 一附加率。 按等额年金法计算: 在式中可知,分子部分是按单利计算n期后本息和。然 后将n期后的本息和分为几等分,再加上附加率。 租金总额∑R=1199836(元) 例如,某租赁项目概算成本为5000万元,租赁双方商定 纳入概算成本的租赁费为: 分5年10期偿还租金。从起租日起,以后每隔半年等额偿还 1199836-1182102=17734(元) 一次,年利率10%,附加率5%,求每期租金和租金总额。 17734 实际费用率=101500=1.747% 因P=5000万元,r=5%,n=10,每半年支付一次租赁 4.按照租期把费用率换算成年费率,再纳人利率计算。 费,故i=年利率/2=10%2=5%,代人公式得: 由于3年6次付租,承租人平均占用期限=(0.5+1+ 平均每期租金: 1.5+2+2.5+3)/6=1.75年,年费率=1.5%/1.75%= R=500×(1+10×5%)+5000×59%=1000(万元) 10 0.86%,再加入年利率=10%+0.86%=10.86%,以此计算 租金总额为: 利率: 10R=10×1000=10000(万元) 租金总额=∑R=1198409(元) 年金法(Annuity Method)指以现值概念为基础,将一 租赁费=1198409-1182102=16307(元) 项租赁资产在未来各租赁期间内租金金额按一定的比率予 程货费率“0600=1.681% 以折现,使其现值总和恰等于租赁资产的概算成本。年金法 是按照每期复利一次的方法来计息的。 上述计算方法中,第一种较为普遍,对承租人有利:第二 设某一租赁项目的概算成本为P,分n期偿付租金,每期 种不尽合理,除非利率十分优惠:第三、四种,从资金占用角 利率为i,每期复利一次,未来各租赁期间内的租金分别为 度讲是有道理的,但第四种在年利率上加年费率,如果租期 R,R2,R,…,R。,每期租金中所含概算成本额分别为P, 长,租金总额要增大。 P2,…,P。若按每期期末支付租金,根据复利计息方式,各 期租金R(G=1,2,…,n)与各期租金中所含的成本额P之 租金计算方法(Computational Method of Rent) 间应有如下对应关系: 租金计算方法根据租赁契约的不同商定,有很多的计算 R=P(1+i),R2=P2(1+i)2,…,R。=Pn(1+i)" 方法,分类也不完全一致。目前,国际上常用的租金计算方 将上式变成R为P的函数形式,即为 法有附加率法和年金法两种。年金法又分为定额年金法和 A= 。R2 R。 变额年金法两种,而在变额年金法中又可分为等差递减变额 (1+)…P。= (1+)” 四种。每一种方法又可分为期初先付与期末后付和不规则 将以上n个等式相加,得 支付的形式。期初先付,是指承租人在各个付租间隔期间的 R 期初支付租金。此种支付方式,第一期租金在起租日即需支 B+P2+…+P。=t+0++…+1+i 付。国外一般采用此办法。期末后付,是指承租人在各个付 假设此项租赁资产在n期租金中全部收回,不留残 租间隔期间的期末支付租金,亦称租金后付。此法使租金支 值,则 付时间向后推迟一个间隔期,为资金短缺的承租人提供了方 R R R. 便。我国一般采用此种付息方式。所谓不规则支付,是指第 P=B+B+R=中+++…+0+讨 一次采取先支付(或后支付),其他各次采取后支付(或先支 从上式可以看出,各期租金R,R,…,R。,是以不同的 付)的方法。另外,还有残值为零和不为零,收取一定比例的 折现系数,1,1 保证金或免收保证金,含有宽限期的租金计算方法。不同的 1++1十)分别予以折现,其和恰等 支付租金形式,不同的租金计算方法,支付租金的数额各不 于概算成本P,这是年金法的本质特征。 相同。 在年金法中,根据每次偿还租金是否相等,又分为等额 附加率法(Added Ratio)指在租赁资产概算成本上, 年金法和变额年金法,其计算方式也各不相同。 再附加一项特定的比率(此比率一般由出租者内部掌握)计 等额年金法(Equal Annuity Method)指各期支付的租 算支付租金的方式。附加率法采用每期期末等额支付租金, 金是均等的,数额始终不变,即R,=R2=…=R.。在货币时 按单利计算n期后本息和的方法。计算公式为: 间价值的观念的基础上,每期租金支付的时间不同,支付金 R=P.1+n边+p, 额也不同。因此等额年金法又有期初付租和期末付租,以及 有付租宽缓期的期末付租之分。下面介绍等额年金法先付
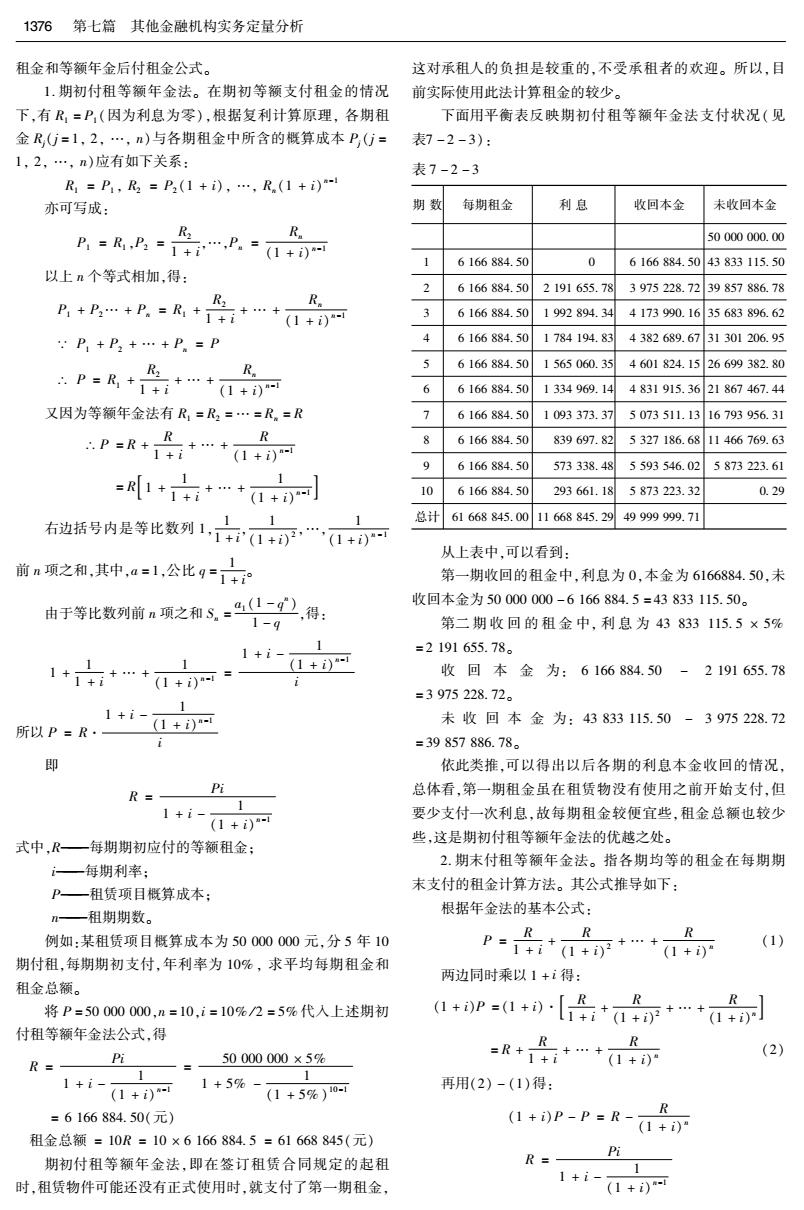
1376第七篇其他金融机构实务定量分析 租金和等额年金后付租金公式。 这对承租人的负担是较重的,不受承租者的欢迎。所以,目 1.期初付租等额年金法。在期初等额支付租金的情况 前实际使用此法计算租金的较少。 下,有R=P(因为利息为零),根据复利计算原理,各期租 下面用平衡表反映期初付租等额年金法支付状况(见 金R,j=1,2,…,n)与各期租金中所含的概算成本P,G= 表7-2-3): 1,2,…,n)应有如下关系: 表7-2-3 R=P,R2=P2(1+i),…,R(1+i)- 亦可写成: 期数 每期租金 利息 收回本金 未收回本金 R2 P=R,B=+…P= R。 50000000.00 (1+i)可 6166884.50 0 6166884.50 43833115.50 以上n个等式相加,得: 6166884.50 2191655.78 3975228.7239857886.78 R2 R。 B+B+P.=R+++0+ 6166884.50 1992894.34 4173990.1635683896.62 P+P2+…+P。=P 6166884.50 1784194.83 4382689.6731301206.95 R2 R 6166884.50 1565060.35 4601824.1526699382.80 .P=R+1+i …+ (1+i)可 6 6166884.50 1334969.14 4831915.3621867467.44 又因为等额年金法有R,=R2=…=R。=R 6166884.50 1093373.37 5073511.1316793956.31 P=R+是++a 6166884.50 839697.82 5327186.6811466769.63 (1+i)可 9 6166884.50 573338.48 5593546.02 5873223.61 1 1 =1+++…+0+) 10 6166884.50 293661.18 5873223.32 0.29 右边括号内是等比数列1,中+“,(1+) 11 总计61668845.0011668845.2949999999.71 从上表中,可以看到: 前n项之和,其中,a=l1,公比q=+ 1 第一期收回的租金中,利息为0,本金为6166884.50,未 由于等比数列前n项之和9.=-》,得。 收回本金为50000000-6166884.5=43833115.50。 1-9 第二期收回的租金中,利息为43833115.5×5% 1 =2191655.78。 收回本金为:6166884.50-2191655.78 =3975228.72。 1 所以P=R· 1+i-1+i网 未收回本金为:43833115.50-3975228.72 =39857886.78. 即 依此类推,可以得出以后各期的利息本金收回的情况, R= Pi 总体看,第一期租金虽在租赁物没有使用之前开始支付,但 1 1+i-0+i) 要少支付一次利息,故每期租金较便宜些,租金总额也较少 式中,R一每期期初应付的等额租金; 些,这是期初付租等额年金法的优越之处。 2.期末付租等额年金法。指各期均等的租金在每期期 i—每期利率: P—租赁项目概算成本: 末支付的租金计算方法。其公式推导如下: 根据年金法的基本公式: n一租期期数。 例如:某租赁项目概算成本为50000000元,分5年10 R p▣+++沙+…++ (1) 期付租,每期期初支付,年利率为10%,求平均每期租金和 两边同时乘以1+i得: 租金总额。 R 将P=50000000,n=10,i=10%/2=5%代入上述期初 付租等额年金法公式,得 R Pi =50000000×5% =R+++ (2) R=- 1+i- 1 (1+i) 1+5%- (1+59%)10可 再用(2)-(1)得: (1+)P-P=R-+ R =6166884.50(元) 租金总额=10R=10×6166884.5=61668845(元) Pi 期初付租等额年金法,即在签订租赁合同规定的起租 R=- 1 1+i 时,租赁物件可能还没有正式使用时,就支付了第一期租金, (1+i)可
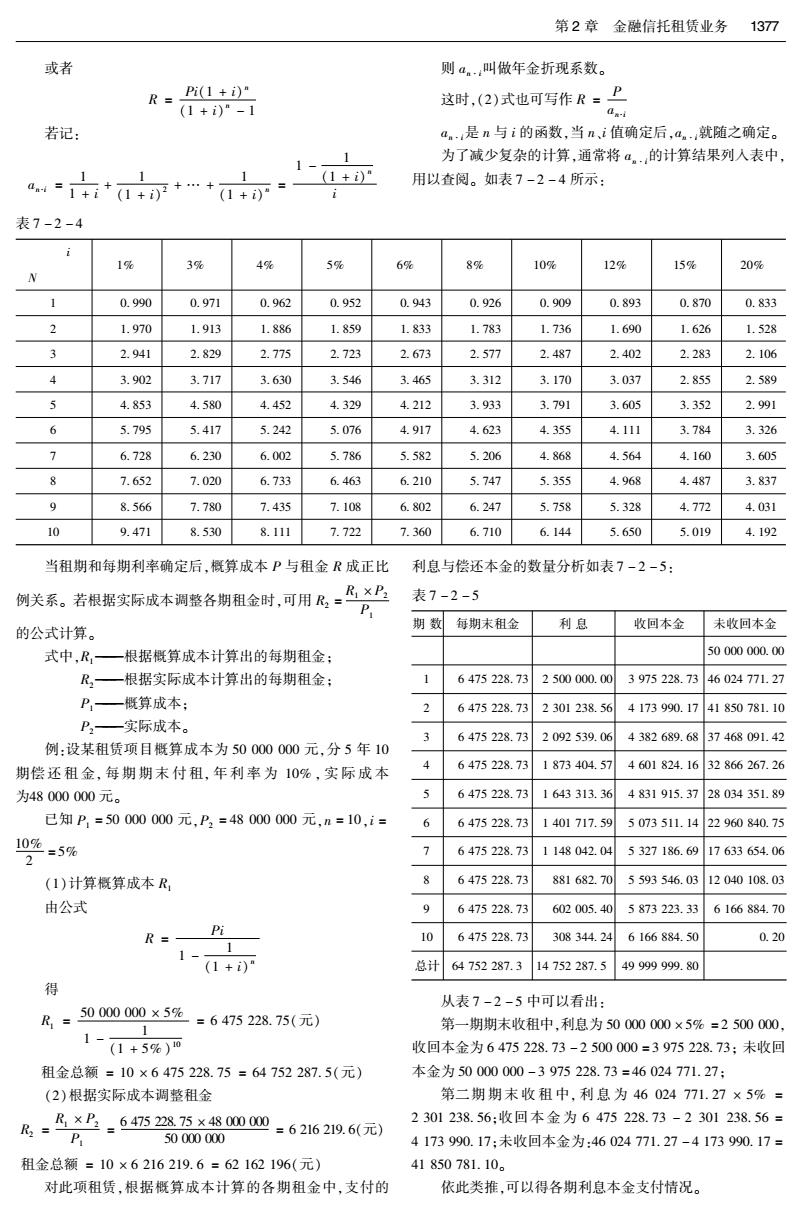
第2章金融信托租赁业务13刀 或者 则a。叫做年金折现系数。 R= Pi(1+)" (1+i)"-1 这时,(2)式也可写作R=P Ga-i 若记: a.是n与i的函数,当n,i值确定后,a。.就随之确定。 为了减少复杂的计算,通常将a。的计算结果列人表中, 1- a+t++…+1+一一0+D 用以查阅。如表7-2-4所示: 表7-2-4 1% 3% 4% 5% 6% 8呢 10% 12% 15% 20% 1 0.990 0.971 0.962 0.952 0.943 0.926 0.909 0.893 0.870 0.833 2 1.970 1.913 1.886 1.859 1.833 1.783 1.736 1.690 1.626 1.528 3 2.941 2.829 2.775 2.723 2.673 2.577 2.487 2.402 2.283 2.106 4 3.902 3.717 3.630 3.546 3.465 3.312 3.170 3.037 2.855 2.589 5 4.853 4.580 4.452 4.329 4.212 3.933 3.791 3.605 3.352 2.991 6 5.795 5.417 5.242 5.076 4.917 4.623 4.355 4.111 3.784 3.326 7 6.728 6.230 6.002 5.786 5.582 5.206 4.868 4.564 4.160 3.605 8 7.652 7.020 6.733 6.463 6.210 5.747 5.355 4.968 4.487 3.837 9 8.566 7.780 7.435 7.108 6.802 6.247 5.758 5.328 4.772 4.031 10 9.471 8.530 8.111 7.722 7.360 6.710 6.144 5.650 5.019 4.192 当租期和每期利率确定后,概算成本P与租金R成正比 利息与偿还本金的数量分析如表7-2-5: 例关系。若根据实际成本调整各期租金时,可用R,。×上 表7-2-5 P 期数 每期末租金 利息 收回本金 未收回本金 的公式计算。 式中,R,一根据概算成本计算出的每期租金; 50000000.00 R,一根据实际成本计算出的每期租金: 6475228.73 2500000.00 3975228.73 46024771.27 P一概算成本; 2 6475228.73 2301238.56 4173990.17 41850781.10 P,一实际成本。 3 6475228.73 2092539.06 4382689.68 37468091.42 例:设某租赁项目概算成本为50000000元,分5年10 期偿还租金,每期期末付租,年利率为10%,实际成本 6475228.73 1873404.57 4601824.16 32866267.26 为48000000元。 6475228.73 1643313.36 4831915.37 28034351.89 已知P,=50000000元,P2=48000000元,n=10,i= 6475228.73 1401717.59 5073511.1422960840.75 10%=5% 6475228.73 1148042.04 5327186.69 17633654.06 2 (1)计算概算成本R, 6475228.73 881682.70 5593546.03 12040108.03 由公式 9 6475228.73 602005.40 5873223.33 6166884.70 R=- Pi 10 6475228.73 308344.24 6166884.50 0.20 1- 1 (1+i)" 总计 64752287.3 14752287.5 49999999.80 酸 从表7-2-5中可以看出: R= 50000000×5% -=6475228.75(元) 1 第一期期末收租中,利息为50000000×5%=2500000, 1- (1+5%)0 收回本金为6475228.73-2500000=3975228.73:未收回 租金总额=10×6475228.75=64752287.5(元) 本金为50000000-3975228.73=46024771.27: (2)根据实际成本调整租金 第二期期末收租中,利息为46024771.27×5%= 2301238.56:收回本金为6475228.73-2301238.56= R2= B×2=647522875×48000000=6216219.6(元) P 50000000 4173990.17:未收回本金为:46024771.27-4173990.17= 租金总额=10×6216219.6=62162196(元) 41850781.10。 对此项租赁,根据概算成本计算的各期租金中,支付的 依此类推,可以得各期利息本金支付情况

1378第七篇其他金融机构实务定量分析 在表中最后一期未收回本金为0,或者远远小于1的小 1 1 数,这是小数点后两位的误差,是允许的:此表与期初付租等 面十=4十+十可= 额年金法比较,多支付一期利息,故而每期末租金大于期初 中i+(1+可+…++=a 1 1 1 租金,租金总额相应增加。此种租金计算法,虽然是期末付 租但要多支付租金。 1 1 1 ++1++…+1+m+0+=a 1 变额年金法(Variable Annuity Method)指每期租金 1 不等,逐年发生一定规律变化的租金计算方法。根据租金逐 故片++动+品++可 年变化规律的不同,可分为等差变额年金法和等比变额年 金法。 a4+…+a-ln4+a4=∑a 期末付等差变额年金法(Arithmetical Variable Annuity 所以,P=Ra4+ndal-d∑a mmediate Payment Method)指租金从第二期开始,每期 第一期租金计算公式: 租金比前一期增加一个常数d的租金计算法。等差变额年 R=(P+d∑a)-nd 金法又分为等差递增变额年金法和等差递减变额年金法。 设每期租金分别为R,R2,R,…,R。,则 又因为∑a4=a14+a24+…+a R1=R,R2=R+d,R=R1+2d,R.=R1+(n-1)d 1- 1 将上选试代入P=冬+n++的年 i i +…+1+i) 金基本式中,则有: =市140*1+刷 P品+器 (1+)” =a-a) ++++aa可 d 所以有 +2n*…+, p+a-小d i (1+i)" 因为等差变额年金的租金从第二期开始,每期都比前一 在上式右边问时加减一个分式兴+分++ 期增加一个d,这个常数d是租赁双方在租赁契约上商定好 的,所以,第一期租金计算出来后,各期租金就容易求得了。 即 当d>0时,每期租金总比其前一期租金增加一个正数, 这种租金计算叫等差递增变额年金法;当d<0时,每期租金 p=[++a十++a+Ja 总比其前期租金增加一个负数,这种租金计算称等差递减变 +++…+a 2d 额年金法,当d=0时,各期租金相等,即等额年金法。 (1+i)" +供+物+物*+ 将d=0代入R=P+4∑a)-d式中,得 R,=上(P+0×∑)+nx0= -兴++a*+刷 nd aa 1 1- =+a++ 1 而a4=一1+) (1+) i aa 1 所以, P Pi R1= 1 +0+品+…别 +_n-2 1- 1 (1+)“ (1+)9 1-(1+i 又因为十+十+++可= 1 1 由此可见,等额年金法可称为变额年金法的特殊情况。 例:某一租赁项目概算成本为50000000元,分5年10 +品+品+…+时 期期末偿还租金,年利率为10%,租赁双方商定每期递增 1 1 1 1 600000元支付租金,求第一期租金和租金总额。 “中*1++…+a++1+*0++… 将P=50000000元,n=10,i=10%=59%,d=600000 2 *a**可*…*a+ 1 1 元代入RP+a-小d中,有: 1 ++i+1+++i