
例2(P.12例3)一个盒子中装有10个大小、形状完全相同的晶体管, 其中3只是次品.按下列两种方法抽取晶体管: (1)先任取一只,作测试后放回盒中,再任取下一只,二 有放回抽样 (2)先任取一只,作测试后不放回,在剩下的中再任取一只. 试分别对这两种抽样方法,求从这10只晶体 无放回抽样 管任取2只中,恰有一只是次品的概率. 解设A={抽取的2只晶体管中恰有一只是次品} (1)有放回抽样:由于每次都是从10只中取一10×10种取法 即2的样本点数n=102, 古典概型 一共有7×3+3×7=42种取法 P()=42 100 (2)无放回抽样:第1次是从10只中取,第2次是从9只中取, 即2的样本点数n=10x9,古典概型 10×9种取法 A一共有7×3+3×7=42种取法 P(A= 90
(2)先任取一只, 作测试后不放回, 在剩下的中再任取一只. 一个盒子中装有10个大小、形状完全相同的晶体管, 其中 3 只是次品. 例2 (P.12 例3) 按下列两种方法抽取晶体管: (1)先任取一只, 作测试后放回盒中, 再任取下一只; 有放回抽样 试分别对这两种抽样方法, 求从这10只晶体 无放回抽样 管任取2 只中,恰有一只是次品的概率. 解 设 A={ 抽取的 2 只晶体管中恰有一只是次品} (1)有放回抽样: 由于每次都是从10只中取 —— 1010 种取法 即 的样本点数 n= 102 , 第 1次取到合格品,且第2 次取到次品 第1次取到次品,且第2 次取到合格品 A: —— 7 3 —— 3 7 —— 共有 73 + 37 = 42 种取法 古典概型 . 100 42 P(A) (2)无放回抽样: 第1次是从10只中取, 第2次是从9只中取, 即 的样本点数 n= 109, —— 109 种取法 A:—— 共有 73 + 37 = 42 种取法 古典概型 . 90 42 P(A)
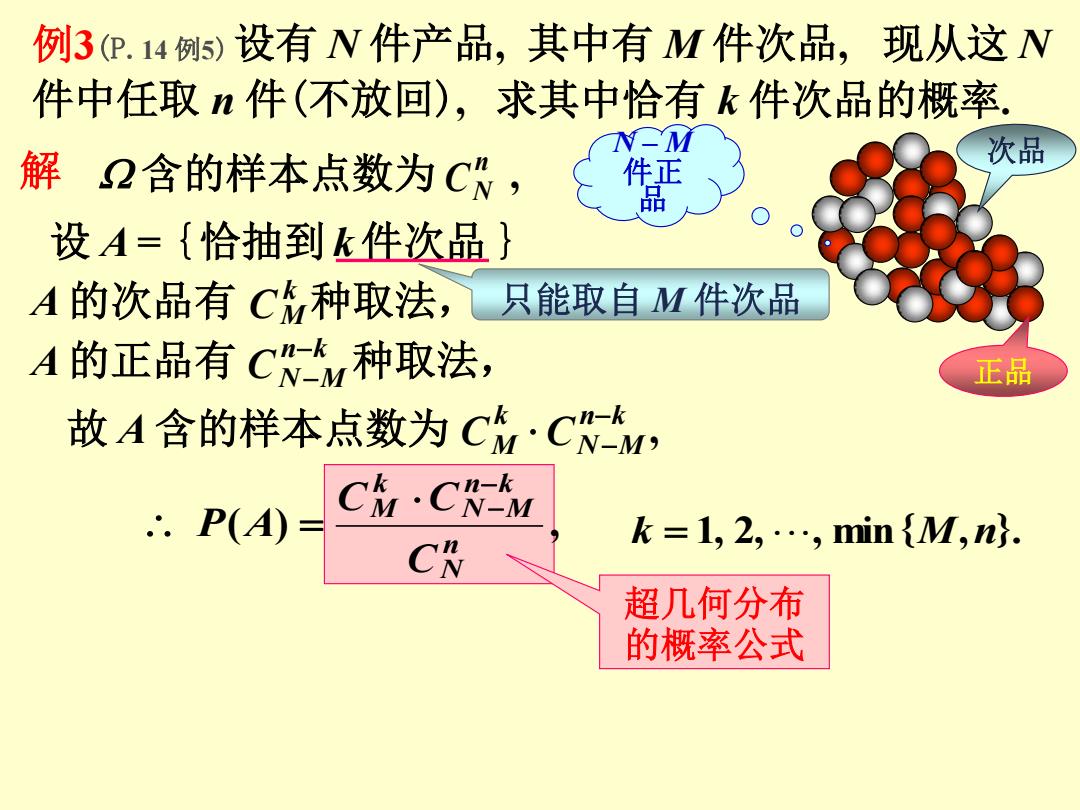
例3P.14例)设有N件产品,其中有M件次品,现从这N 件中任取n件(不放回),求其中恰有k件次品的概率. N- 解2含的样本点数为C, 次品 品 设A={恰抽到k件次品} A的次品有C种取法,只能取自M件次品 A的正品有CM种取法, 正品 故A含的样本点数为C·CM, ∴.P(A)= C·CM k=1,2,…,min{M,n. 超几何分布 的概率公式
现从这 N 件中任取 n 件(不放回), 设有 N 件产品, 其中有 M 件次品, 解 ( ) , n N n k N M k M C C C P A 例3(P.14 例5) 设 A = {恰抽到 k件次品 } 求其中恰有 k 件次品的概率. 次品 正品 N – M 件正 品 含的样本点数为 , n C N A 的次品有 C M k 种取法, 只能取自 M 件次品 A 的正品有 C N n k M 种取法, 故 A 含的样本点数为 , n k N M k CM C k 1, 2, , min{M,n}. 超几何分布 的概率公式