
《高等数学》下册教案 第十二章无穷级数 定理2、(比较审效法)设正项级数∑“、∑y,则 (1)若un≤.(n),且∑y.收敛,则∑u。也收敛: 2若,≥(n),且∑y.发教,则∑4,也发教。 证:1)四为立.收敛,由定理1,部分和亿}有解,即T,≤M(n):又因为么,≤对所有 的n都成立,且,的部分和为S,则 Sn=4+4++n≤y+%+…+。=Tn≤M 表明部分和数列S,}有界,从而由定理1,级数∑4枚敛: 注:实际上定理2中的不等式只要从菜个N开始满足即可。 侧2时论p-气数空行的族款性, 解:已如调版款空岩是发教的:由的1可知,当p>时,级数空》放数:故只风右考多p 的情形。当n<1时,<m,市>片根据定理2,当p<1时纸款三》发放,由光得封重 的站货数 例3、利用一级数的敛散性以及比较审敛法,判别下列级数的敛散性。 1 2am+切 n+2 台nn+) 解:分:p=21,所以款站:空行:P1,所以线数空行发: 含0用5n京p1,做板款空行林:根据比较审效法 1 1 11 饭数空+n心 1一也收: 三品品-片p叶,线杂碧,家北发车我击数款 第6页一共32页 惠床安
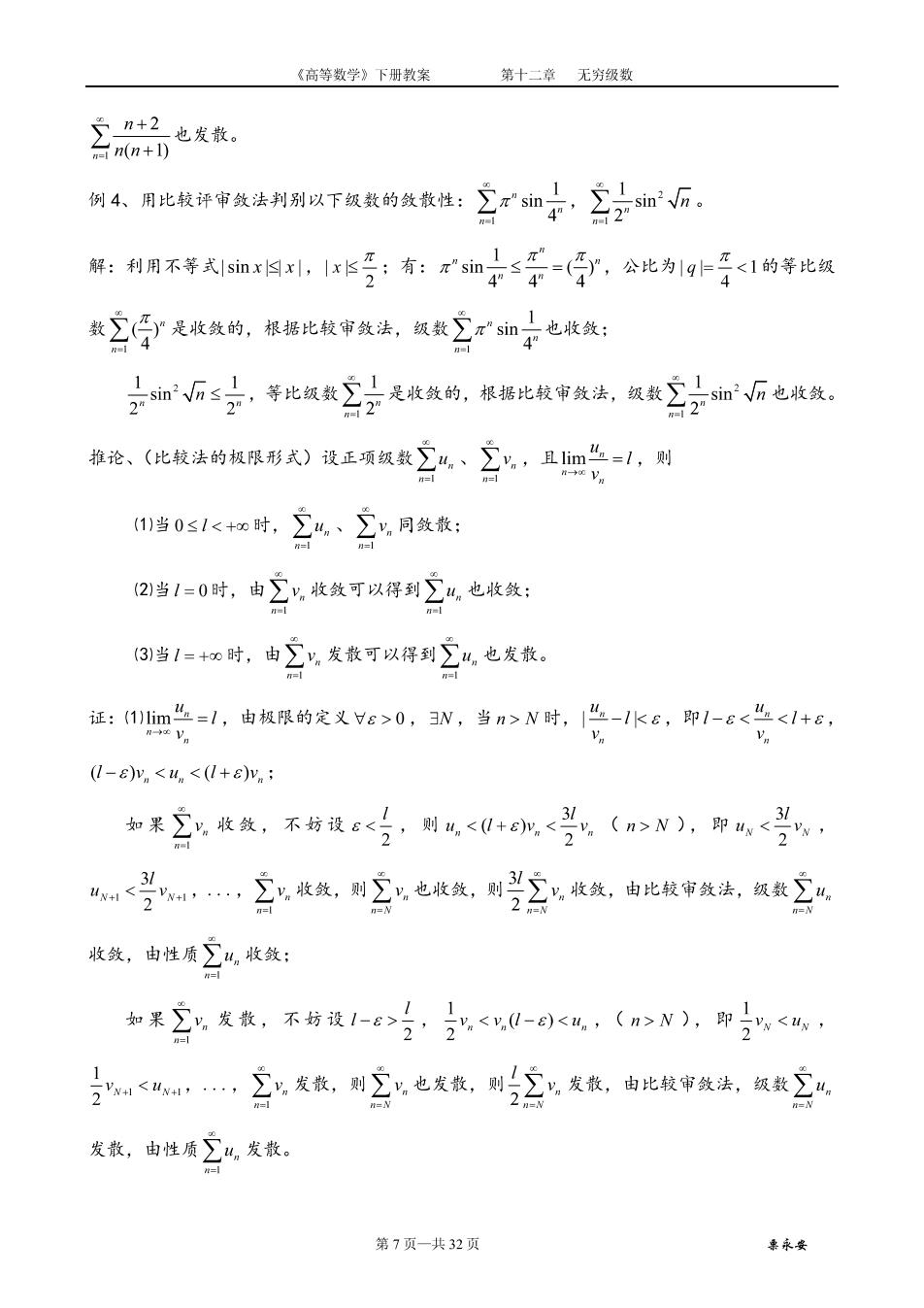
《高等数学》下册教案第十二章无穷级数 例4、月比蚁许审线法制别以下领数的做教性:立女s如子,三血瓜。 新:利周不等式s血x国,1号:有:s如≤子=原,公比为g非<1的等比板 数立孕是报放的,根据比较审级法,复款立:©如子也放微: 子65宁等比饭款分光报线的,根第比俊甲线法,板款宁面6色收数。 台2” 教论、(化做法的城限影式)镜正项纸数2、立,且m受=山,则 当0≤1<时,24、2同袋核: 2当1=0时,由∑y收敛可以得到∑“,也收敛: 3当1=+0时,由∑y,发教可以得到∑4,也发散。 运:登=,由报限的交义ve>0,3,当a>N时,总-水ke,脚1-e<总<1+e, 0-ey。<.<+Ey 如果立散数,不持设G行,明<0:6城<兰(>N).甲,兰, “<…发货,则,也收敛,则么成货,由比较审纸法,复数立0 收敛,由性质,收数: 如果公发教,不纷设1-8>行,<%0-,(n>N),即, <“…立发款,则三,也发教,则三发载,由比酸审铁法,饭数立u 发款,由性质公,发数。 第7页一共32页 基永安

《高等数学》下册教案 第十二章无穷级数 例5、讨论级数2sm上与∑l+力)敛教性. :老时m,+小→0以利内f=10之 立m与同数款,回为空引发数,故空如色发散: n 三+宁与宁网数2字:空0+中地数 网6,为泰空。a0)物我 :0<a1时,以=710:a1时,=-0: 0as1时,么+发款:0>1时,+7微数 定理3、(化位审线法,达期员尔料别法)设空是正项板数,巴=P, p<1时,板数技数:2p>1(钱血=)时,饭款发教。 证:=会0,由规限的定义:VG>0,3V,m>N时,-pK8,或m>N时。 p-6p6 1们p<1时,可以进择e,使得p+e=a<1,,从而41<a,n>N时,即 ux<aux,uv<au<au,ux<a'us,... 级数∑auw=山,∑a是公比a<1的等比级数,从而∑auw收敛,根据比较审敛法,饭数 山+山w+3+…收敛,由性质级数∑,收敛。 注:①如果P=1,则比值审敛法失效,可改用定理1或2进行判别: ②用比值审敛法时,必须求出比值的极限P,再根据P进行判别。 第8页一共32页 泰承安

《高等数学》下册教案 第十二章无穷级数 的7节纸空学空品 a+)的线散性。 ,=2"+ 2n° ”-1 n-1 n+n++W+2 timlim (n+D(+1 nnm+D四m-n+2)=5m0-+) 2 1 比值法失效,改用比较法判别: 2”ada8以空,w空品 n-1 n-I 1 故原领数乞刀=1发数。 台n(n+l) 注:错解:1= n2 +万收致。 定理4、(根值审敛法,柯西判别法)设∑4,是正项级数,m=P 1)p<1时,级数收致:2p>1时(或im=∞)时,级数发散。 温:①可以证明,如果血会一小.则达有▣面-1,表明北值法夫黄时不可荐用振位 ②以上的各种判别法,只适用于正项级数,且各自有一定的适用范围,但也有其局限性。可 以进一步建立更为有效的审敛法,此过程可以无休止的进行下去,但判别的过程也将越发 复杂。 二、绝对收敛与条件收敛 定义、设∑“,为任意项级数,如果正项级数∑4,收敛,则称级数∑“,为绝对收敛:如果 正项级数∑山,发散,但级数∑山,本身收敛则称级数∑山。为条件收敛。 第9页一共32页 基永安

《高等数学》下册教案第十二章无穷级数 创带快空学是香他时 解:版款立9是-个任意项纸数,时于正项板款立吗巴1,国为有四5分,两 收载,根据正项纸数的比散审发法,立收益,由定义,战数立吧为绝对收位。 定理5、绝对收敛的级数自身一定收敛,即如果级数∑山,收敛,则级数∑4,一定收敛。 温:将版空,活中-u-化28的中空是三:因 为颜数“,|敢教,故由正项级款的比较审敛法。级数,股教,且∑2枚纸:根据性质 “收敛级数的提项和构成的级数仍然收级”,可知级数∑(2,-u,D收敛,即∑4,收数。 注:①根据定理5,对于绝对收敛的级数,只需要使用正项级数的审敛法即可,从而相当的 一类级数的敛散性的讨论转为正项级数敛散性的讨论。 ②一般如果∑4,发散,推不出级数∑山,一定发散:但是如果∑山,的发散性是用根值法或 比位法骑之的,是时可以山空以发数拉始空,发数:例,因为回->1,所以 交u发数,对ve>0,议,当n>N时,侣p水,中p-ep+e:由于 >1,可以取道当的,使得p-e>.即>p->1,浅以.从百>N时。 利,}单调增加,因此im,≠0,必有im,≠0:根据级数收敛的必要条件∑4,发散。 ③绝对收敛的级数的许多性质是条件收敛的级数所不具备的,如任意调整原级数中项的位置 后的新级数仍然收敛,且和不变:两个绝对收敛的级数的柯西乘积所组成的新级数仍然绝 对收敛,且其和为原来的两个级数的和的乘积。 三、交错级数审敛法 交错级数:4-4+4,-山+…+(-)-4+…=∑(-)-4。,其中4,>0,n: 第10页一共32页 票来安