
936第五篇证券投资实务定量分析 定数量的某种货币,以交换另一种特定数量的货币。例如,如 注释: 果这位美国投资者有一张1000万日元大额存单,六个月后到 :一期末的汇率,以每单位国内货币能兑换成的国外货币数 期,那么,这名投资者可能会签订一项远期合约,在六个月后 表示: 交割1000万日元,换回8100000。用远期外汇合约,这名投 。—期初的汇率,以每单元国内货币能兑换成的国外货币数 资者就消除了任何与汇率变动有关的未来风险。 表示: 确定远期外汇汇率的一种方法就是认为它是未来即期外 外汇汇率的百分比变动: 汇汇率的无偏估计。即: hr—外国的通货膨胀率: EL (DC/FC)]FLf DC/FC)] hp一国内的通货膨胀率: (1) 式中,E[,(DC/FC)]一在时刻1时外汇今天的远期汇率; R。,心一一期后到期的无违约风险债券的国外收益率: F1)—远期汇率: F[(DC/FC)]一在时刻1时外汇的即期汇率的 F—现行汇率和远期汇率间的百分比差额。 均值。 资料来源:Bruno Solnik的著作International Investment,.(第2版) 如果这种假设是正确的,那么承担外汇风险就会降低收 (Reading:MA:Addisom-Wesley Publishing Co.l991),第9页。 益率。在一段时间内,由外汇带来的利得被损失所抵消。因 系。可以从中看出,不同国家的即期汇率、远期汇率、利率及 此,一些人论证认为不提供期望收益的风险应该被套期保值。 通货膨胀率之间都是相互关联的。但是,这些关系都只是理 换句话说,即用远期市场对外汇风险套期保值实际上从长远 论上的,那么实际中又将是什么样的情况呢? 来看应该是无成本的。 债券久期(Bond Duration) 债券国际投资的利率平价(Interest Rate Parity of 从一般意义讲,所有证券都要承担利率风险,并且长期 Bond International Investment) 证券比短期更为敏感。然而,人们常常不注重期限度量,忽 利率平价在远期汇率的变动和名义利率之间建立了某种 视债券中间的时期的现金流,仅仅关注到期时的最后支付。 联系。这是另一种估计汇率的方法。具体来说,利率平价可 利息支付(中间时期现金流)对于利率风险是重要的,而且 以表示为: 众所周知票息高的债券比那些票息低的债券对利率的敏感 F.=-1≌Re-R. (1) 性要低。实质上,通过更快的现金流回报,持有高票息债券 f(FC/DC) 式中,F⅓一远期汇率和现行即期汇率之间的百分比差额。 的投资者比持有低票息债券的投资者可更快收回投资。 这样,远期汇率和即期汇率之间的百分比差额就近似地 敏性的影响是有限的。然而,久期这种度量可以让人 等于外国名义利率和国内名义利率之间的差额。例如,如果 评价具有不同现金流动方式的证券的相对承担利率风险的 英镑对美元的即期汇率为1.67£/$,一年期远期汇率为0.7 成分,因为它既考虑到期末的又考虑到期间的现金支付情 £/$,那么我们可以估计出英国和美国间的利率差异为: 况(它使债券定价定理5得以精确化)。 (0.7£/8)/(0.67£/$)-1=0.0448或4.48% 图5-1-13,用具有3年内同一水平的现金流的假设 证券说明了久期度量的基本概念。注意,该假设证券平均 具体来说,根据利率平价,英镑相对美元而言将贬 值4.48%。 生命期为2年,如图上部所示。然而,一个更加精确的现金 图5-1-12有助于弄明白这些平价关系之间的相互关 流生命度量,会考虑到现金流的现值。在这种情况下,日标 是用支付的现值给每次支付加权而不是简单地用未加处理 即期汇率 的钱数来计算平均时点。这种用每次支付的现值为每次支 =(0低)-1 付时间加权的度量被命名为久期d,它在图的下部得以说 购买力平价 远期汇率期望 明。由于较早的支付比较晚的支付现值高,因此久期将小 E(sp)-E(hg-hp) F()=E(S) 于平均生命期。 《 通货膨胀率 远期汇率 计算一个债券的久期类似于计算一个债券的价格,计算 RF,R一RDm=ESk) hg-hp F=[F(fLXfx0]-1 的公式如下: T T C Rn.FC-Rn.DC-E(hg-hp) F&-RnFC-Rn.DC 国际费雪关系 利率平价 +*p (1) 利息率 公式(1)包括排列出现金流系列的现值并用每只现金流 Rn.PC-Rn.DC 发生的时期为其自身加权。现金收入包括利息C和赎回本金 图5-1-12国际平价关系:线性关系 F,并且时间加权数是从1到。最后,这些时间加权现金流的 和除以价格P,P得自于债券估值公式

第1章债券投资业务 937 F 续表 债券C(票息): d=[(100)+2(1)+3(罗]no0 =[1(90)+2(81)+3(827)]100=2733 1000=2.7年 久期和利率灵敏度(Duration and Interest Rate Sensitivity) 作为一种度量投资者投资回收期的方法,久期同期限相比,其 时间 最明显的优势表现在度量债券价格相对于到期收益率变化的 灵敏度上:久期使债券定价定理2得以精确。通常认为两支 平均生命期 不同期限的债券,其到期收益率变化1%,所带来的债券价格 (a) 变化,期限较长的变化大于期限较短的变化。然而,如果债券 的票息不同,上述结论则不正确。而且任何情况下在期限与 价格灵敏度之间不存在一种简单的关系,而久期却给了一个 更为接近的度量: 价格变化的百分比=久期×到期收益率变化 1/到期收益率 为进一步说明,我们可从表5-1-16中利用票息债券C。 时间 记得我们为票息债券计算出一个2.7年的久期。而且我们能 2 再假定利率从10%增长到11%。用这些债券的输入,可得到 久期 (6) 期望的价格变化: 图5-1-13a)每支现金流的平均寿命b)现金流的久期 ¥-)-27)-25% 1.10/ (2) 表5-1-15用公式(1)来计算三只假定证券的久期。折 久期得出的度量在利率变化幅度较小时很有效,但一旦 价债券A的久期3年,这与它的期限相同。零票息折债券期 利率变化变较大时,就会失去其精确性。假定的100个基点的 限与久期相同,是因为全部的现金流在持有期末收到。另一 变化在短期内也是相对比较大的变化。同样,我们可以推论: 方面,期间发生支付的债券其久期短于期限。因此,票息债券 如果所评价的预期利率和价格变化是在一个较短的预测时期 C的久期为2.7年,小于期限3年。债券B由于其平均现金流 内进行的,如1-6周,那么分析工作可做到最好。 而拥有更短的久期,为1.9年,因为它在到期之前支付会更多。 表5-1-16列出了在三种不同的票息率12%、14%和 16%条件下不同期限债券的久期。注意:期限较长的债券通 表5-1-15 债券久期的计算 常比期限较短的债券拥有更大的久期。例如14%利率水平 下,一只20年的债券票息为10%,其久期为6.98,同样条件下 d=[()+2(号)+3( 10年债券久期为5.68,5年债券久期为3.7。同时要注意,高 利率水平下的久期低于低利率水平下的久期。例如:20年的 债券A(折价): 债券在14%利率水平下,久期为6.98,而在12%利率水平下, 久期为7.74,在16%利率水平下久期为6.30。 d=[(9o小2(9)+3(上】n0w 表5-1-16 久期、票息率和到期收益率 =[10)+20)+3100)]n00=6=3年 票息率 到期年限 6% 8% 10% 12% 债券B(抵押): 收益率=12% 1 0.93 0.92 0.92 0.92 J 4.05 3.91 3.78 3.68 d=[(00)2()3(】n0 10 6.61 6.23 5.95 5.73 15 7.96 7.46 7.13 6.88 20 8.53 8.05 7.74 7.52 =[1(364)+2(331)+3(301)]100=}929=1.9年 1000 收登率=14% 0.92 0.92 0.91 0.91 3.98 3.83 3.71 3.60
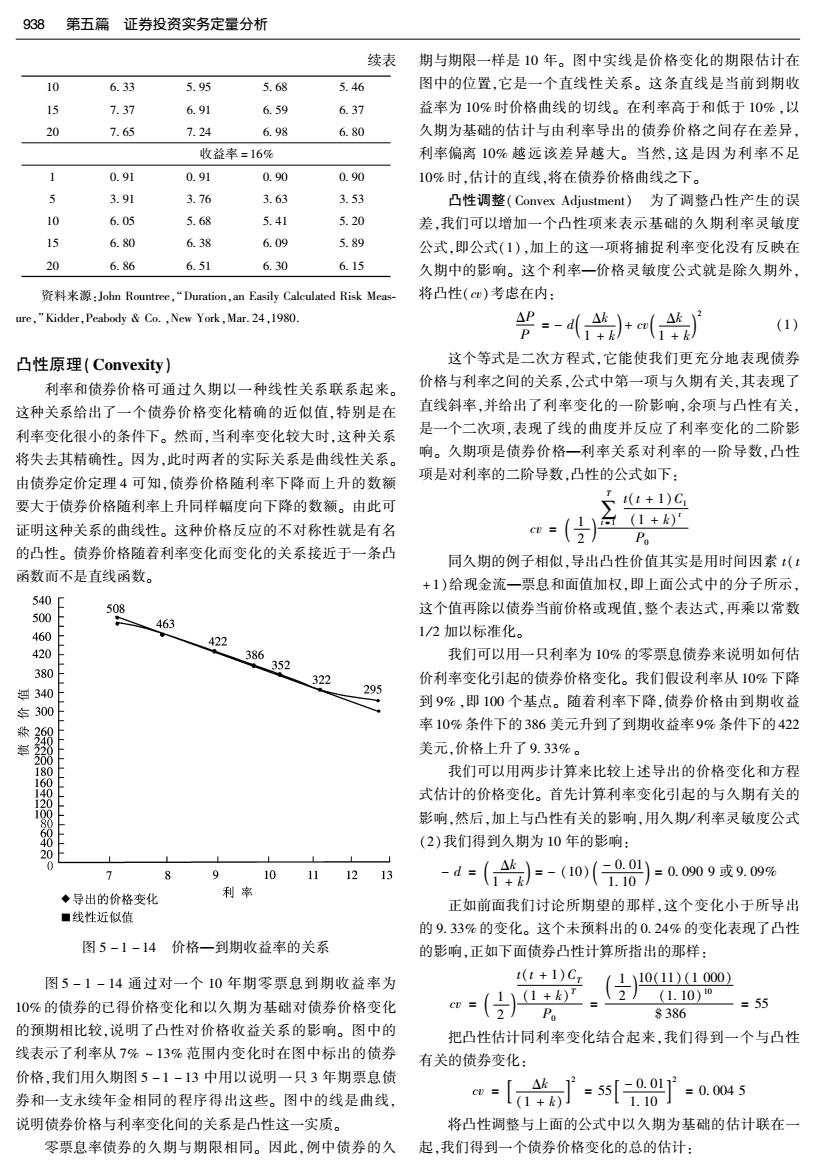
938 第五篇证券投资实务定量分析 续表 期与期限一样是10年。图中实线是价格变化的期限估计在 10 6.33 5.95 5.68 5.46 图中的位置,它是一个直线性关系。这条直线是当前到期收 15 1.37 6.91 6.59 6.37 益率为10%时价格曲线的切线。在利率高于和低于10%,以 20 7.65 7.24 6.98 6.80 久期为基础的估计与由利率导出的债券价格之间存在差异 收益率=16% 利率偏离10%越远该差异越大。当然,这是因为利率不足 1 0.91 0.91 0.90 0.90 10%时,估计的直线,将在债券价格曲线之下。 5 3.91 3.76 3.63 3.53 凸性调整(Convex Adjustment)为了调整凸性产生的误 10 6.05 5.68 5.41 5.20 差,我们可以增加一个凸性项来表示基础的久期利率灵敏度 15 6.80 6.38 6.09 5.89 公式,即公式(1),加上的这一项将捕捉利率变化没有反映在 20 6.86 6.51 6.30 6.15 久期中的影响。这个利率一价格灵敏度公式就是除久期外, 资料来源:John Rountree,“Duration,an Easily Calculated Risk Meas- 将凸性(cw)考虑在内: ure,"Kidder,Peabody Co.,New York,Mar.24,1980. 光-d)*(牛 (1) 凸性原理(Convexity) 这个等式是二次方程式,它能使我们更充分地表现债券 利率和债券价格可通过久期以一种线性关系联系起来。 价格与利率之间的关系,公式中第一项与久期有关,其表现了 这种关系给出了一个债券价格变化精确的近似值,特别是在 直线斜率,并给出了利率变化的一阶影响,余项与凸性有关, 利率变化很小的条件下。然而,当利率变化较大时,这种关系 是一个二次项,表现了线的曲度并反应了利率变化的二阶影 将失去其精确性。因为,此时两者的实际关系是曲线性关系。 响。久期项是债券价格一利率关系对利率的一阶导数,凸性 由债券定价定理4可知,债券价格随利率下降而上升的数额 项是对利率的二阶导数,凸性的公式如下: 要大于债券价格随利率上升同样幅度向下降的数额。由此可 (t+1)C (1+k) 证明这种关系的曲线性。这种价格反应的不对称性就是有名 2 Po 的凸性。债券价格随着利率变化而变化的关系接近于一条凸 同久期的例子相似,导出凸性价值其实是用时间因素t(t 函数而不是直线函数。 +1)给现金流一票息和面值加权,即上面公式中的分子所示, 5400 508 这个值再除以债券当前价格或现值,整个表达式,再乘以常数 500 463 460 1/2加以标准化。 422 420 386352 我们可以用一只利率为10%的零票息债券来说明如何估 380 322 价利率变化引起的债券价格变化。我们假设利率从10%下降 回340 295 到9%,即100个基点。随着利率下降,债券价格由到期收益 年300 斯 率10%条件下的386美元升到了到期收益率9%条件下的422 美元,价格上升了9.33%。 180 我们可以用两步计算来比较上述导出的价格变化和方程 E 式估计的价格变化。首先计算利率变化引起的与久期有关的 100 影响,然后,加上与凸性有关的影响,用久期/利率灵敏度公式 (2)我们得到久期为10年的影响: 20 0 1 8 9 10 1213 -d=()-(0(08)-0009或909% ◆导出的价格变化 利率 正如前面我们讨论所期望的那样,这个变化小于所导出 ■线性近似值 的9.33%的变化。这个未预料出的0.24%的变化表现了凸性 图5-1-14价格一到期收益率的关系 的影响,正如下面债券凸性计算所指出的那样: 图5-1-14通过对一个10年期零票息到期收益率为 1(+1)CT /1110(11)(1000) (2(1.10)0 10%的债券的已得价格变化和以久期为基础对债券价格变化 () =55 Po s386 的预期相比较,说明了凸性对价格收益关系的影响。图中的 把凸性估计同利率变化结合起来,我们得到一个与凸性 线表示了利率从7%~13%范围内变化时在图中标出的债券 有关的债券变化: 价格,我们用久期图5-1-13中用以说明一只3年期票息债 券和一支永续年金相同的程序得出这些。图中的线是曲线, w=厂kJ [a-0 =0.0045 说明债券价格与利率变化间的关系是凸性这一实质。 将凸性调整与上面的公式中以久期为基础的估计联在一 零票息率债券的久期与期限相同。因此,例中债券的久起,我们得到一个债券价格变化的总的估计:
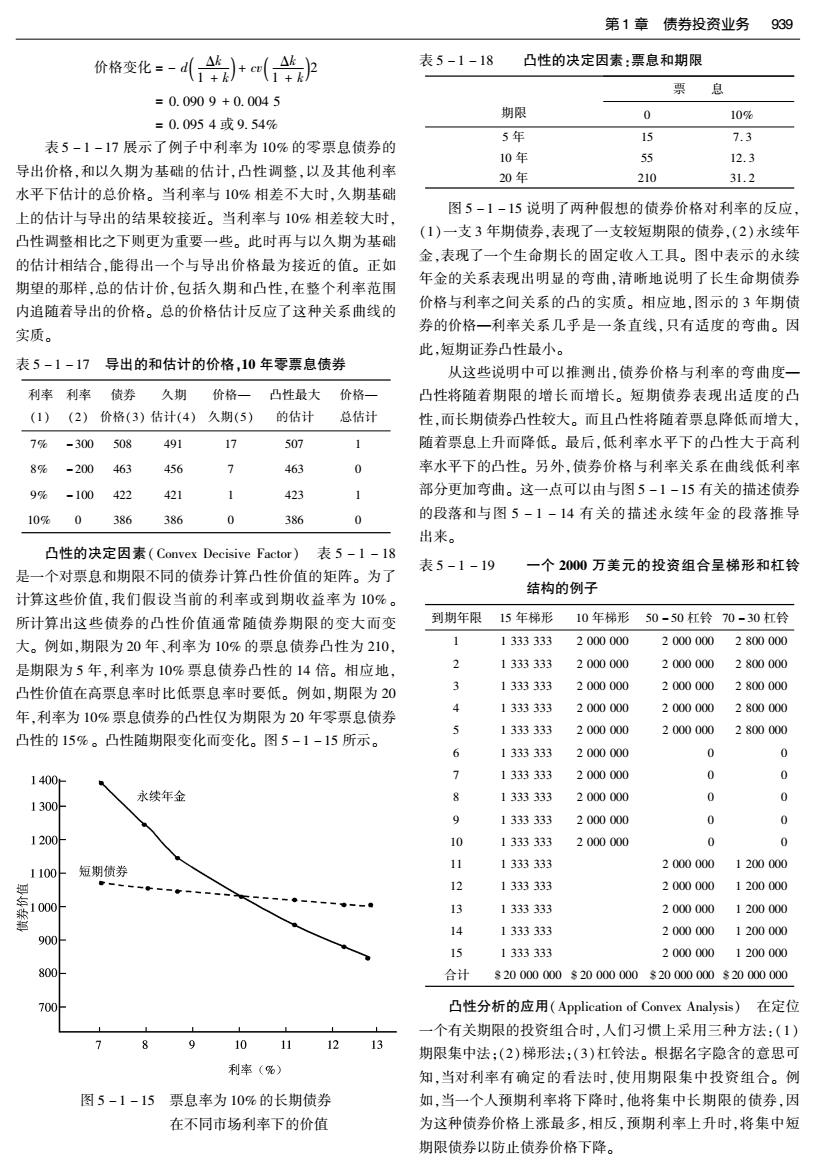
第1章债券投资业务 939 价格变化=-d(牛)+a(牛》 表5-1-18 凸性的决定因素:票息和期限 票息 =0.0909+0.0045 期限 0 10% =0.0954或9.54% 5年 15 7.3 表5-1-17展示了例子中利率为10%的零票息债券的 10年 55 12.3 导出价格,和以久期为基础的估计,凸性调整,以及其他利率 20年 210 31.2 水平下估计的总价格。当利率与10%相差不大时,久期基础 图5-1-15说明了两种假想的债券价格对利率的反应 上的估计与导出的结果较接近。当利率与10%相差较大时, 凸性调整相比之下则更为重要一些。此时再与以久期为基础 (1)一支3年期债券,表现了一支较短期限的债券,(2)永续年 的估计相结合,能得出一个与导出价格最为接近的值。正如 金,表现了一个生命期长的固定收入工具。图中表示的永续 年金的关系表现出明显的弯曲,清晰地说明了长生命期债券 期望的那样,总的估计价,包括久期和凸性,在整个利率范围 内追随着导出的价格。总的价格估计反应了这种关系曲线的 价格与利率之间关系的凸的实质。相应地,图示的3年期债 实质。 券的价格一利率关系几乎是一条直线,只有适度的弯曲。因 此,短期证券凸性最小。 表5-1-17导出的和估计的价格,10年零票息债券 从这些说明中可以推测出,债券价格与利率的弯曲度一 利率利率债券 久期 价格一 凸性最大 价格一 凸性将随着期限的增长而增长。短期债券表现出适度的凸 (1) (2)价格(3)估计(4)久期(5) 的估计 总估计 性,而长期债券凸性较大。而且凸性将随着票息降低而增大, 7% -300 508 491 17 507 随着票息上升而降低。最后,低利率水平下的凸性大于高利 8% -200 463 456 1 463 0 率水平下的凸性。另外,债券价格与利率关系在曲线低利率 9% -100 422 421 423 1 部分更加弯曲。这一点可以由与图5-1-15有关的描述债券 10% 0 386 386 0 386 0 的段落和与图5-1-14有关的描述永续年金的段落推导 出来。 凸性的决定因素(Convex Decisive Factor) 表5-1-18 表5-1-19 一个2000万美元的投资组合呈梯形和杠铃 是一个对票息和期限不同的债券计算凸性价值的矩阵。为了 计算这些价值,我们假设当前的利率或到期收益率为10%。 结构的例子 所计算出这些债券的凸性价值通常随债券期限的变大而变 到期年限 15年梯形 10年梯形 50-50杠铃70-30杠铃 大。例如,期限为20年、利率为10%的票息债券凸性为210, 1333333 2000000 2000000 2800000 是期限为5年,利率为10%票息债券凸性的14倍。相应地, 1333333 2000000 2000000 2800000 凸性价值在高票息率时比低票息率时要低。例如,期限为20 3 1333333 2000000 2000000 2800000 年,利率为10%票息债券的凸性仅为期限为20年零票息债券 4 1333333 2000000 2000000 2800000 1333333 2000000 2000000 2800000 凸性的15%。凸性随期限变化而变化。图5-1-15所示。 6 1333333 2000000 0 0 1400 1 1333333 2000000 0 0 永续年金 8 1333333 2000000 0 0 1300 1333333 2000000 0 0 1200 10 1333333 2000000 0 0 11 1333333 2000000 1200000 1100F 短期债券 12 1333333 2000000 1200000 13 1333333 2000000 1200000 14 1333333 2000000 1200000 900 15 1333333 2000000 1200000 800 合计 820000000$20000000$20000000$20000000 700 凸性分析的应用(Application of Convex Analysis)在定位 一个有关期限的投资组合时,人们习惯上采用三种方法:(1) 10 12 13 期限集中法:(2)梯形法:(3)杠铃法。根据名字隐含的意思可 利率(%) 知,当对利率有确定的看法时,使用期限集中投资组合。例 图5-1-15票息率为10%的长期债券 如,当一个人预期利率将下降时,他将集中长期限的债券,因 在不同市场利率下的价值 为这种债券价格上涨最多,相反,预期利率上升时,将集中短 期限债券以防止债券价格下降

940 第五篇证券投资实务定量分析 收益率曲线 同时长期债券价格上升为110.88,短期债券仍为100。因此, 10 杠铃形投资组合价值为110.88×50%+100×50%=105.44, 是两个端点的中值。这两种投资组合价值的差异(105.44- 9 105.09=0.35)就是由凸性造成的。这个差异值就是来自于 8 杠铃形投资组合的利润,即当利润下降时杠铃形投资组合比 集中的投资组合所多具有的绩效。正常条件下,当收益曲线 向上倾斜时,这35个基点的差异,被短期债券的损失所掩盖。 1 但当收益曲线平坦时,凸性的贡献将赋于杠铃形投资组合全 5 10 20 30 期限(年数) 部的优势。 当然反过来也对:预期利率上升时杠铃形投资组合不被 图5-1-16扁平收益曲线,激发我们的杠铃形战略 看好。集中化投资组合比久期相同的杠铃形投资组合价格下 梯形和杠铃投资组合在表5-1-19中得以说明。15年 跌幅度小。 和10年期的梯形投资组合收入被均匀分割,每个收到和被投 资的现金数值都相同。这种期限结构使得在利率周期内每年 债券久期的计算公式(Bond Duration Calculation 得到平均的回报,并暗示投资组合经理没做利率预测。相比 Formula) 之下,杠铃形的投资组合中,即有短期债券,又有长期债券,却 久期计算等式,可以单独置于展开表的一个单元中(展开 没有投资于中间期限的债券,如表5-1-19中所示。杠铃形 表指列示新证券的发售价、总价差、股息或利息等的表):因 投资组合如人们所料那样比梯形投资组合流动性好,这是因 此,可以很容易地进行敏感性分析。 为比较侧重于短期债券。而且收益曲线向上倾斜时回报较 下面的这个公式弹性很强,可适应任何非半年付息复利 多,也因为更多的基金投资于长期债券。 计算。这一周期计算公式可以很方便地安排到展开表中去, 当收益曲线扁平时,杠铃形结构具有特别的吸引力。每 如下: 一个到期的收益几乎完全一样。图5-1-17说明一个1989 年8月30日的收益曲线结构。通过侧重于期限的两个极端, .+立宁X了-(立an小(÷jn 长期和短期,使其回报有能超过梯形投资组合或者集中于中 e{(1+中-小(中m 间期限的债券。这种提高回报可能性的原因之一就是凸性。 (1) 随着利率变化,债券价格沿着一条向上倾斜的凸曲线轨迹运 式中,C—一每期用美元支付的利息: 动,这种影响对于长期债券最为明显。 一从上一次支付开始本次利息期已经消逝的部分: 为进一步说明,我们比较两个具有同样久期如5年,但组 n—一剩余的总的利息支付期: 成部分不同的投资组合。一种是只买5年期债券,即投资组 Par一债券的面值: 合。另一种,把投资的一半用于购买国库券,另一半用于长期 Panp一每年总的利息支付期(例如,抵押是典型的每 债券,为便于说明,认定它为10年期债券。这种一半长期、一 月支付,所以p=12)。 半短期相结合的方法,产生了一个久期为5年的杠铃形投资 虽然上述表达方式看起来杂乱无章,但它更易被安排进 组合(0.5×0久期+0.5×10年久期)。 展开表中。久期和凸性公式要求对不同的期限进行总计。例 112 如,计算30年期,半年付息的展开表要求对60次现金流量进 110.88 杠铃形投资组合 行贴现。而公式(1)可以置于一个单元格中,并可以用于任何 婆 (50%短期/50%长期) 105.44 杠铃形 期限的债券(也适用于任何频率的支付)。 车106 -105.09一集中化 =0.35=利润 集中化投资组合 债券凸性计算公式(Bond Convex) 100≤ (100%中间期) 根据泰勒扩展序列公式,债券价格变化能近似地表述 0 10 久期(年数) 如下: 图5-1-17杠铃形投资组合获得凸性的益处 业=器由+号祭(+ (1) 资料来源:Francis H.Trainer,Jr.,Sanford C.Barnstein&Co 式中,e一(d)3及其以上的各高阶小量的和。 图5-1-17中实线表示了久期在0-10年范围内变动 因此 时,价格的反应。假设所有债券到期收益率下降100个基点, 号-器虚+分器日(+号 (2) 也就是说整个收益曲线下移1个百分点。当利率下降100个 公式(2)等号右边第一项就是由持续期决定的债券价格 基点时,5年债券或者是集中化的投资组合的价值为105.09。 变化,而等号右边第二项包含了债券价格在市场收益率为i时