
第1章债券投资业务931 且有可能比仅在国内投资更进一步地减少风险。 样,像加拿大和德国间0.11的相关系数就允许通过国际分散 因为国际市场彼此之间是非高度相关的,所以国际投资 化来明显地减少风险。实际上,等权数加权组合资产的标准 比仅投资于美国国内各行业更能降低风险。图5-1-8中例 差小于任何单个国家组合资产的标准差。(见表5-1-14)。 示的是在1969至1989年间几个国家的指数。这些指数表明 这一组合资产的标准差计算如下: 全部来自某一特定国家的股票组合资产的业绩高低。而且, 表5-1-14 相关系数 这些指数都把1969年12月份的值定为100。因此,投资于英 相关系数 国(UK)的$100在1989年末值$1200。我们假定每个国家 加拿大 德国 英国美国 都是等值投资,而且我们观测到了一种比任何国家的投资组 加拿大 1.0 合的波动性都小的组合资产证券。 德国 0.11 1.0 1400 加拿大 英国 0.37 0.35 1.0 1200 德 国 美国 0.63 0.41 0.61 1.0 1000 英 国 Source:Based on Morgan Stanley Capital Interational Indexes. 800 美国 2=(1/4)2(0.201)2+(1/4)2(0.210)2+(1/4)2(0.272) 藏600 +(1/4)2(0.161)2+2(1/4)(0.201)(0.210)(0.11) 400 +2(1/4)(1/4)(0.201)(0.272)(0.37) 200 +2(1/4)2(1/4)(0.201)(0.161)(0.63) +2(1/4)(1/4)(0.210)(0.272)(0.35) 0 Dec. Dec. Dec Dec. Dec. +2(1/4)(1/4)(0.210)(0.161)(0.41) 1969 1974 1979 1984 1989 +2(1/4)(1/4)(0.272)(0.161)(0.61) 时间 =0.002525+0.002756+0.004624+0.001620 图5-1-8各国家指数及平均线(每个国家的投资都相同) +0.000580+0.002529 Source:Morgan Stanley Capital International Indexes 标准差为0.157(0.024753的平方根)。 从图5-1-8中我们可以看出,国际分散化有助于稳定 国际债券的发行方式(Issue Mode of Treasury Bill) 组合资产,图中的平均线的波动明显很小。表5-5-14中对 国际债券的发行方式可分为“公开发行”(公募)和“内部 单个国家的资产组合及这四个国家等权数加权资产组合的收 发行”(私募)两种。 益的均值和标准差进行了比较。我们假定每个国家的组合资 1.公开发行。借款人先与国际性大银行或证券公司联 产都投资于同样的证券。等权数加权组合资产的均值收益是 系,初步确定债券发行的条件,选定牵头银行,然后组成一个 各国家组合资产收益的简单平均数。另一方面,等权数加权 银行集团包销。再由银行集团或证券公司向广大投资者推 组合资产的标准差(或波动性)有赖于各单个资产(在此例中 销。这种债券可在公开市场上流通、买卖。采用这种方式发 指国家组合资产)的相关性。 行债券,如借款者系官方机构(中央或地方政府)必须提供该 现计算组合资产的方差: 国(或该地区)的经济政治局势、对外贸易、国际收支、国际储 =d+2,W, 备、对外负债及财政金融等详细资料和统计数字。如借款人 系企业,必须提供该企业的资产负债表、企业活动成果等详细 式中,i广一单个国家的资产组合。 情况。公开发行的债券一进入流通市场,债券就会随着市场 利率的波动和债券供求情况的变动而变动。这是因为: 表5-1-13精选指数收益的均值和标准差 (1)债券行市与票面利率成正比,但与市场利息率成反 美元 比。以公式表示为: 均值 标准差 加拿大 12.2% 20.1% 债务行市=务囊 德国 14.8% 21.0% (2)债券行市受债券供求的影响。债券需求即投资者承 英国 16.2% 27.2% 购债券的愿望,债券供应即已发债券的出售和发行新债券。 美国 11.5% 16.1% 如果供过于求,行市就会下跌:反之,则上涨。 等权数证券组合 13.7% 15.7% 2.内部发行。借款人将债券交由一定范围(如几个大银 表5-1-13中列出了这些指数相关性。由于缺乏高度正 行或大证券公司)的投资者承购。借款人只同几家银行直接 相关,这说明可以通过国际化投资来降低风险。一国国内各 交易。这种债券不公开出售,也不在市场上流通,采取记名方 种股票资产组合间的相关程度非常高,一般都高于0.95。这 式,由少数金额机构认购。采用这种方式,借款人可较少地公

932第五篇证券投资实务定量分析 开自己企业的资料和统计数字。 手续费以及发行差价(实际发行价格与票面价格之差)三者之 和。一般不在发行成本的基础上计算发行成本年率,以便与 国际债券收益率(Yield Rate of Treasury Bill) “借款成本”相比较,从而判断哪一种方式更为有利。这是债 国际债券收益率是国际债券认购者在债券上的收益与其 券发行者必须计算的一个指标。 投入本金之比。这不但是对投资者利益攸关的指标,也是债 1.发行成本和计算。发行债券的成本,主要分利息、各项 券发行者所应该关心的指标。债券收益对债券投资者来说, 手续费以及发行差价三个部分。其中各项手续费又可分为: 是决定债券对他是否有吸引力的主要因素。因为投资者在购 最初费用(包括债券印刷费、广告费、律师费、牵头人杂费、包 买债券之前就把该债券的收益率与银行存款的利息和股权投 销手续费、代理人手续费、债券上市税金以及债券登记手续费 资的收益率相比较,从而判断向哪个方向投资更为有利。因等)、付息手续费,还本手续费等。发行成本的计算公式为: 此,债券收益率的高低与该债券能否顺利发行和销售有着密 发行成本=(年利息+年付息手续费)×平均发行年限+ 切关系,发行者在债券发行前也应该对此作一些估算。债券 :最初费用+发行差价+还本手续费 收益率通常有三种: 例如,某公司在日本发行一笔公募债券,发行额为100亿 1.名义收益率。指债券每年应付利息占债券面值的百分 日元,发行差价99.5%,票面利率7.6%,平均发行年限9年, 比,即债券息票上注明的利率: 包销手续费1.8%,登记手续费0.03%,代理人手续费0.15%, 2.即期收益率。指投资者买进债券时债券利息与买进债 其他最初费用2500万日元,还本手续费0.125%,付息手续费 券实际价格之比。可用下列公式计算: 0.25%。则这笔债券的发行成本如下: 。V×I 利息及利息手续费: y.= P一×100% (1000000×7.6%)×(1+0.25%)×9=685710(万日元) 式中,y。一即期收益率; 最初费用: 。—债券面值: 包销手续费=1000000×1.8%=18000(万日元) 【—一债券年利率: 登记手续费=1000000×0.03%=300(万日元) P—债券实际价格。 代理人手续费=1000000×0.15%=1500(万日元) 可见,即期收益率与债券的实际价格成反比。实际价格 其他最初费用=2500(万日元) 越低,即期收益率越高:反之,则越低。 合计:22300(万日元) 例如,发行债券的面值为1000元,购买债券的实际价格 发行差价:1000000×(1-99.5%)=5000(万日元) 为900元,债券年利率为5%,即期收益率为: 还本手续费:1000000×0.125%=1250(万日元) 1000×5%×100%=5.56% 发行成本总计=714260(万日元) y.= 900 2.发行成本率的计算。计算出发行成本以后,就可在其 3.归还期内平均收益率。指债券持有人将债券始终保存 基础上按如下公式计算发行成本率: 直至还本期满所能得到的实际收益率。可用下列公式计算: 发行成本 x1+上 发行成本率=发行预-(最初费用一发行差价】×平药发行年限 ym = 1 T×100% 将上例中的数据代入此公式: 2(+P 发行成本率= 714260 式中,y。一债券归还期内平均年收益率: 1000000-(22300-5000)x9×100%=84.59% V。一债券面值: 即这笔债券的发行成本率为84.59%。 —债券年利率: P一债券的实际价格: 分散化投资的百分比风险法(Risk Percentage Ap- T一债券的归还期(年)。 proach of Investment Decentralization) 例如,债券面值为1000元,购买债券的实际价格为950 “百分比风险”表示当额外地随机把证券加入时,一般股 元,债券的年利率为10.25%,归还期为20年,则债券归还期 票的标准离差的降低(假定加入的股票权数都相等)。 内的年平均收益率为: 图5-1-9表述了当增加证券的数量时,组合资产的方差 1000×10.259%+1000-950 就会减少。同样的原理也可以应用于国际组合资产证券。图 y= 2×(1000+950) 1 20—×100%=10.7% 5-1-9例示了国内分散化和国际分散化中的利得。是以百 分比来说明了风险的降低。也就是说,“百分比风险”衡量的 是分散化后的一般股票的总风险百分比。具体来说,如果σ: 国际债券的发行(Issue of Treasury Bill) 表示一般股票的标准差,σ。表示股票组合资产的标准差,那么 国际债券自发行直至还清本息期间所支付的利息、各项百分比风险可以表示为:
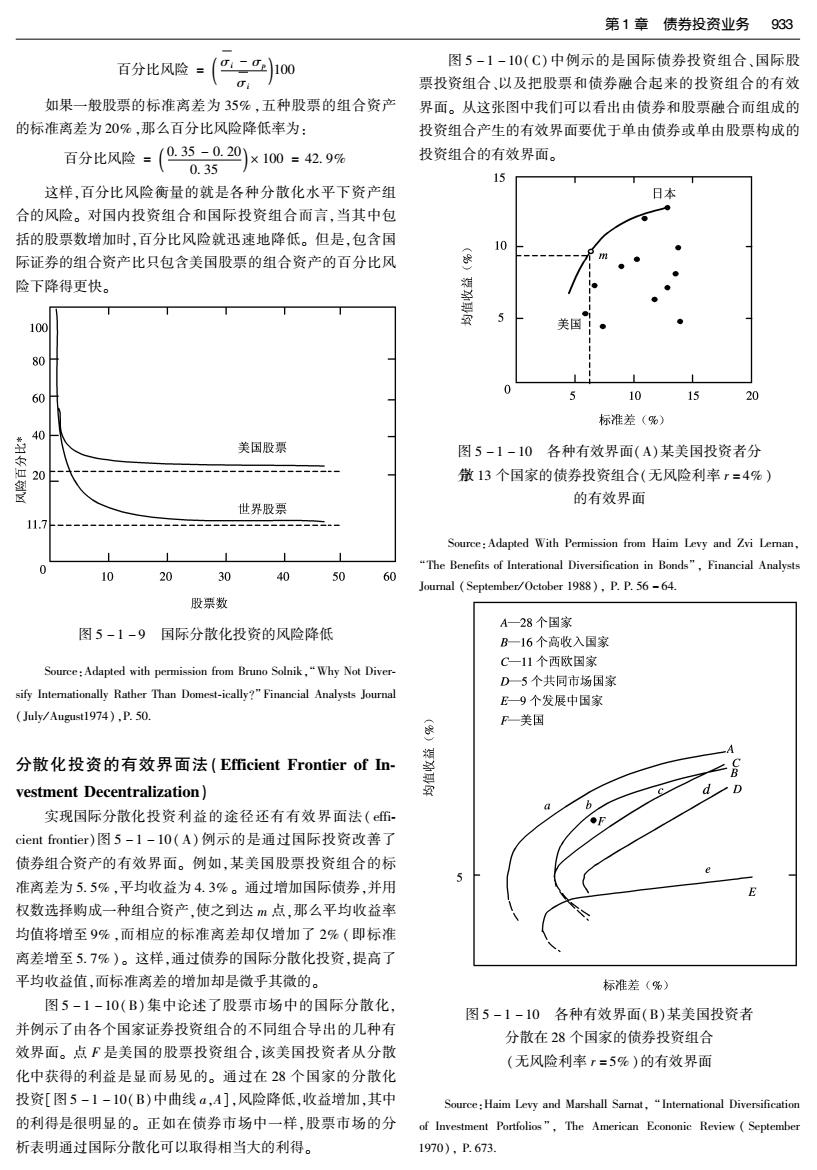
第1章债券投资业务933 百分比风险 图5-1-10(C)中例示的是国际债券投资组合、国际股 票投资组合、以及把股票和债券融合起来的投资组合的有效 如果一般股票的标准离差为35%,五种股票的组合资产 界面。从这张图中我们可以看出由债券和股票融合而组成的 的标准离差为20%,那么百分比风险降低率为: 投资组合产生的有效界面要优于单由债券或单由股票构成的 百分比风脸-(色829x10:29瞬 投资组合的有效界面。 15 这样,百分比风险衡量的就是各种分散化水平下资产组 日本 合的风险。对国内投资组合和国际投资组合而言,当其中包 括的股票数增加时,百分比风险就迅速地降低。但是,包含国 10 际证券的组合资产比只包含美国股票的组合资产的百分比风 平 险下降得更快。 100 美国 0 60 0 10 15 20 标准差(%) 40 美国股票 图5-1-10各种有效界面(A)某美国投资者分 匹20 微13个国家的债券投资组合(无风险利率r=4%) 的有效界面 世界股票 11.7 Source:Adapted With Permission from Haim Levy and Zvi Leman, 1 "The Benefits of Interational Diversification in Bonds",Financial Analysts 10 20 30 90 50 o Journal September/October 1988),P.P.56-64. 股票数 A一28个国家 图5-1-9国际分散化投资的风险降低 B一16个高收入国家 C一11个西欧国家 Source:Adapted with permission from Bruno Solnik,"Why Not Diver- D一5个共同市场国家 sify Intemationally Rather Than Domest-ically?"Financial Analysts Journal E9个发展中国家 July/August1974),P.50. (5) F一美国 分散化投资的有效界面法(Efficient Frontier of In- vestment Decentralization) D 6 实现国际分散化投资利益的途径还有有效界面法(f- ●F cient frontier)图5-1-10(A)例示的是通过国际投资改善了 债券组合资产的有效界面。例如,某美国股票投资组合的标 准离差为5.5%,平均收益为4.3%。通过增加国际债券,并用 权数选择购成一种组合资产,使之到达m点,那么平均收益率 均值将增至9%,而相应的标准离差却仅增加了2%(即标准 离差增至5.7%)。这样,通过债券的国际分散化投资,提高了 平均收益值,而标准离差的增加却是微乎其微的。 标准差(%) 图5-1-10(B)集中论述了股票市场中的国际分散化 图5-1-10各种有效界面(B)某美国投资者 并例示了由各个国家证券投资组合的不同组合导出的几种有 分散在28个国家的债券投资组合 效界面。点F是美国的股票投资组合,该美国投资者从分散 (无风险利率r=5%)的有效界面 化中获得的利益是显而易见的。通过在28个国家的分散化 投资[图5-1-10(B)中曲线a,A],风险降低,收益增加,其中 Source:Haim Levy and Marshall Sarnat,"International Diversification 的利得是很明显的。正如在债券市场中一样,股票市场的分 of Investment Portfolios",The American Econonic Review(September 析表明通过国际分散化可以取得相当大的利得。 1970),P.673

934 第五篇证券投资实务定量分析 20 系,假定我们有某种不受交易条件限制的国际性贸易商品(比 ▣债券 日本 如铝)。也就是说,假定我们在国际上交易铝无需运费或其他 。股票 15H 债券和股票 费用。像以前一样,让我们用DC表示国内货币(下面的8), 股票。 用FC表示外国货币(如下面的£,即英镑的符号)。这样 Pac表示是今天以国内货币表示的铝的价格,Pac表示的是 10H ·日本 今天以外国货币表示的铝的价格。 债芳 如果可以在国际上交易,并且不发生费用,那么将预测 美国· ◆ 出,经过外汇汇率调整后,铝在国内市场或国外市场上的价格 是相同的。即: Pac=(今天的外汇汇率)Pac (1) 10 15 20 25 30 35 其中今天的外汇汇率是以每一单位外国货币表示的国内 标准差(%) 货币数。例如,如果铝的销售价为0.65£,并且今天的外汇汇 图5-1-10各种有效界面(C)某美国投资者 率为$1.5385/£,那么美国的预期的铝价格应该是: 分散在13个国家的债券和股票 ($1.5385/£)(0.65£)=81.00 投资组合的有效界面 如果在美国铝的价格不是$1,那么就可以赚得套利利 润。例如,如果美国的实际价格是$1.01(仍然假定不发生交 Source:Adapted with Permission from Haim Levy and Zvi Lerman, 易费用),那么我们可以在英国以0.65£的价格购进铝(汇率 "The Benefits of International Diversification in Bonds,Financial Analysts 为$1.5385/£),并在美国以$1.01的价格卖出,这样我们 Journal (September/October 1988),P.56-64. 从每镑铝中就可获利1美分。 图中的点表示来自不同国家的债券构成的投资组合,方 现在假定下一年中,美国的通货膨胀率为3%。英国的通 块表示来自不同国家的股票构成的投资组合。 货膨胀率为5%。如果通货膨胀是对铝价格的惟一影响,那 么,我们将预测到铝价格如下: 债券国际投资的货币风险估计(Currency Risk Esti- P.e=(1+国内通货膨胀率)Pac mate of Bond International Investment) =(1+0.03)$1 (2) 用国内货币(R)表示的国外投资的收益率可以用下式来 =$1.03 计算: PFc=(1+国外通货膨胀率)P。c R,=在(DCFC) (Dc/FC1+R,)-1 £=(1+0.05)0.65 (3) (1) £=0.6825 =(1+Ra)(1+R)-1 为了保持国际市场的均衡,由方程(1)可知,在年末必 式中,.(DC/FC)一在时刻n时以国内货币表示的外国货 须有: 币的汇率: Pc=(一年后的外汇汇率)Pac (4) 。(DC/FC)一在时刻0时以国内货币表示的外国货 在我们这一个关于铝的例子中,必须有: 币的汇率: $1.03=(一年后的外汇汇率)(0.6825£) R,一国内货币表示的股市上的收益率; 解出外汇汇率可得: R。一外币表示的股市的收益率。 一年后的外汇汇率=$1.03/0.6825£ 例如,假定加拿大的收益率为11.5%,并且加拿大元正日 =s1.5092/e 益坚挺。美元和加拿大元之间的汇率变动是+3.5%。也就 这样我们就可看到,英国较高的通货膨胀率使外汇汇率 是说,在变动3.5%后,每一加拿大元比美元更值钱,以公式 降低(即英镑贬值)。 (1)为基础。美元的收益率为: 我们还可以把这一分析扩展到通货膨胀的一般水平,因 Ro=(1+0.035)(1+0.115)-1 为其他商品也要进口或出口。而且,我们不知道一年后的实 =0.154或15.4% 际通货膨胀率或外汇汇率将为多少。因此,这种关系是建立 在预测值的基础之上的。一般地,外汇汇率的均值和通货膨 债券国际投资的购买力平价(Purchasing Power Par~ 胀率的均值之间的关系被称为购买力平价。这种关系可以表 ity of Bond International Investiment) 示如下: 购买力平价是指两个国家的通货膨胀率和这两个国家的 [1+E(国内通货膨胀率)]/[1+E(国外通货膨胀率)] 外汇汇率之间的关系。这种平价关系用预期的通货膨胀率为 =E(一年后的外汇汇率)/今天的外汇汇率 依据来估计汇率。为了表明通货膨胀率和汇率之间的适当关 也就是说,1加上通货膨胀均值的比率等于外汇收益的均

第1章债券投资业务935 值。上面的表达式有点雄于解释。因此,大多数分析家用的 (1+国内名义利率)(1+国内实际利率) 都是下面的线性近似公式。 (1+国外名义利率)(1+国外实际利率) E[f(FC/DC)] (1+国内通货膨胀率) E(sf)≡ fo(FC/DC) -1兰E(hc-hc)(5) (1+国外通货膨胀率) 其中E是均值的符号,s是外汇现货市场上的收益,以每 注意,通货膨胀率实际上是通货膨胀率的均值。 单位国内货币可以兑换成若干外国货币来表示。f:(FC/DC) 我们预期实际利率是相同的。否则,资金将从实际利率较低 是年末的外汇汇率,fo(FC/DC)年初的外汇汇率,h是通货膨 的国家移向实际利率较高的国家。如果我们假定两个国家的实 胀率。这一方程基本上说明的是外汇收益率近似地等于通货 际利率相同,那么上面的表示方法可以近似成下面的方程: 膨胀率间的差额。 R-Fe-Rnc≌E(he-hc) (1) 让我们用上面的数据来看一下购买力平价的近似方程是 式中,R一单期债券(无违约风险,国库发行)的名义利率: 如何成立的。在我们的例子中: h一一期的通货膨胀率。 根据国际费雪关系,两个国家的名义利率之间的差额近 fo(FC/DC)=1/f (DC/FC) =1/($1.5385/£) 似等于它们的通货膨胀率的均值之间的差额。例如,如果下 一年英国通货膨胀的均值为5%,美国为3%,那么我们可以预 =0.65£/8 FC/DC)=1/(DC/FC) 测这两个国家中的一年期名义利率间的差额近似为2%。 =1/($1.5092/£) 图5-1-11例示的是根据德国和美国市场的数据绘成的国 =0.6626£/s 际费雪关系。黑条是名义利率间的差额[方程(1)的左侧],白条 并且我们可得: 是实际通货膨胀率间的差额[方程(1)的右侧]。可以看出,在名 义利率的差额和通货膨胀率的差额间有明显的正相关关系。 (0.6626£/$)/(0.65£/$)-1兰0.05-0.03 1.0194-1兰0.02 0.0194≌0.02 因此,由方程(5)给出的近似方程是非常合理的。 那么,在原则上,我们应该能够看出通货膨胀率的均值间 的差异,并得出对未来外汇汇率的估计。但在实践中却有两 -5 ■利率 口通货膨胀 个因素需要考虑:第一,国际贸易并非没有费用。而且实际上 有很明显的贸易壁垒(如关税):第二,实际将要发生的通货膨 8 胀是不可知的。通货膨胀是过去度量出来的。而购买力平价 益台指金宝委壁签莹鉴要盥墨 年份 需要了解的却是未来的通货膨胀差异。然而,虽然这一关系 远不完美,但购买力平价却在外汇市场和通货膨胀差异间建 图5-1-11以德国和美国的利率和通货膨胀率 为依据建立起来的国际费雪关系 立了某种联系,这在某些方面是有用的。 Source:Based on data from the Intemational Monetary Funds Interna- 债券投资的国际费雪关系(Fisher Relationship of tional Financial Staistics Yearbook,various editions. Bond International Investment) “Rates”指德国国库券利率和美国国库券利率之间的差额。“n 国际费雪关系在不同国家间的名义利率和通货膨胀率间 f1 ation”指德国消费价格指数(CPI)和美国消费价格指数间的差额。 建立了某种联系。具体来说,如果我们知道了两个国家的名 义利率。那么我们就可以估计出通货膨胀的均值。通货膨胀 债券国际投资的外汇期望(Foreign Exchange Expec- 率的均值又可用来估计外汇汇率。首先我们可以观测到,在 tions) 存在通货膨胀情况下,投资者将要求获得高于资金的时间价 外汇期望表示的是现行远期汇率和未来即期汇率的均值 值补偿的风险报酬。投资者希望能保障他们投资的购买力水 之间的关系。远期外汇汇率(Forward Foreign Exchange Rate) 平。也就是说,名义利率将等于实际利率加上通货膨胀均值 是指现在确定的在未来的某一特定日期交换货币的汇率。一 再加上通货膨胀对利息支付影响的补偿。即: 种货币转换成另外一种货币的能力对成功的国际组合资产的 名义利率=实际利率+E(通货膨胀率)+(实际利率)[E 管理来说是至关重要的。在许多情况下,投资者都知道他们 (通货膨胀率)] 将不得不在未来的某一日期兑换货币。例如,假定在美国某 上式也可写作: 投资者有一张日元大额存单,六个月后在东京到期。为了满 (1+名义利率)=(1+实际利率)[1+E(通货膨胀率)] 足投资者要求货币波动对他们的证券的影响最小化的愿望, 无论在哪个国家中,这一关系都成立,并且,对外国货币的利 外汇的远期市场应运而生。远期外汇合约(forward foreig即ex 率也有同样的关系,因此,费香于1930年建立了如下的关系: change contract)就是要求投资者在未来某一特定日期交割特