
926第五篇证券投资实务定量分析 持续期小于5年的期限。定期支付利息的债券的持续期 持续期是债券系统风险的指标,在分析和管理债券总风 总是小于其期限。零息债券或一次还本付息债券,持续期与 险时要用到该指标。 债券期限相同。 由于 公式(5)是计算持续期的简化。 1 C+)1-1+)-iy,M,w dP=-1+×DxP。xdi 2(1+i)W (1+i) 因此,债券的新价格为 D= (5) 1 (1+) 1+) P=P。+dP=P。-1+×DxP。×di 式中,P。一市场收益率为i时的债券价格: 公式中的各项与公式(1)的定义相同。 P一市场收益率变动后的债券价格。 表5-1-10的例子可以用公式(2)来计算: 901+0.14)°-(1+0.14)-(0.14)(521 (1000)(5) P=B。+P=B,+×DxP×i为一条直线,是债券 (0.14)2(1+0.14) (1+0.14)3 D=- 价格曲线在市场收益率为i时的切线,如图5-1-3所示: 1 1000 (1+0.14) 价格 0.14 (1+0.14) 902,1950-1.14-0.701.5000 (0.0196)1.9254)+1.9254 1 90[1-1.9254 1000 1.9254 0.14 =90(9.4164)+2596.86 90(3.4331)+519.37 =847.48+2596.86 828.39 9%11% 收益率 =4.158 图5-1-3持续期 实际上,持续期是偿还期、利息率、到期日价格,到期收益 率的函数。持续期与偿还期正相关,而与利息率和到期收益率 由于导数是自变量发生微小变动时因变量变化的量,因 负相关。如果债券的利息率较低,偿还期又长,其持续期要比那 此用持续期去估计债券价格波动是误差的。当市场收益率发 些高利率,短偿还期债券的持续期要长。同时,随到期收益率的 生较大波动时,误差会比较大。例如,一种债券的偿还期为25 上升,持续期将下降。持续期与价格的波动性正相关,因为较长 年,面值为1000元,票面利息率为6%的债券,在市场收益率 的持续期在利率改变时,其价格波动也较大。例如,如果预期利 为9%时价格为(P。)705.36元。当市场收益率提高到11% 率下降,投资者应投资于持续期较长的债券,以获取本利得。 时,债券价格P,按照债券价格公式(1)的计算结果为578.91 dp 1 p=-I+i'D.di (6) 元,下降17.93%。 而按照持续期方法计算的债券价格(P,)将下降21.24% 所以持续期与债券价格变动的大致关系为 -D(△基点) ×(×1.58×2%) △9,=1+100 式中,△P—债券j价格波动的百分比: 平均延续期免疫法(Immunity Method During Aver- D一债券j的持续期: age Last Period) 一债券j的到期收益率。 平均延续期免疫法是避免风险的方法之一。众多的投资 △基点债券j到期收益率的变动程度,即式(6)中的。 者在购入债券时都有确定的目标。要在既定时期获得确定收 这里1%为100个基点。 入以满足支出要求。例如,养老金机构要在退休者到达年龄 等式(6),表明持续期与价格变动正相关。所以持续期长 时付一年费。如果将资金投入债券,而中间利率下降,期终可 的债券比持续期短的债券的价格风险大。公式(6)也可以用 能得不到足够的收人。假设一家养老基金会现在有1000万 前面的例子来说明。债券的持续期为4.16年,现价为 元资本,5年以后需付出1610.5万元养老金,不考虑这段时间 $828.39,假设到期收益率从14%下降至12%,下降了200个 的经营费用,投资者必须使这笔投资的收益包括利息、债息、 基点,债券价格将上升7.3%,至$888.86。即 债券增值等达到10%的年率才行。设想基金会在一开始就购 49=+4)=1.30% 入1000万元年息10%的债券,看起来没什么问题,但如果利 率在这6年中下降,固然债券投资可收到原订的10%债息, 8828.39(1+0.0730)=$888.86 但新获得的债券却只能按较低的利率获得收益,总资金量达
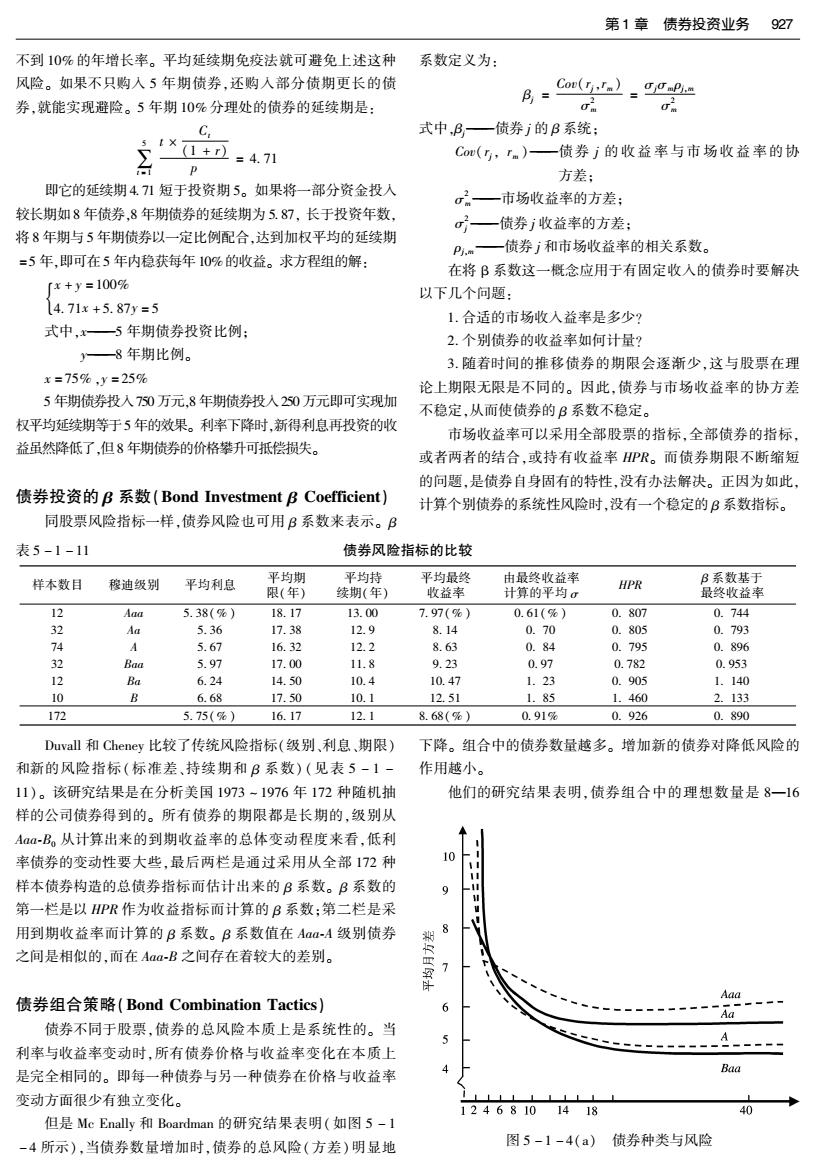
第1章债券投资业务 927 不到10%的年增长率。平均延续期免疫法就可避免上述这种 系数定义为: 风险。如果不只购入5年期债券,还购人部分债期更长的债 β= Cou(y')_ 券,就能实现避险。5年期10%分理处的债券的延续期是: c品 式中,B—债券j的B系统: 5【X 1+=4.71 Co(,Tm)一债券j的收益率与市场收益率的协 方差: 即它的延续期4.71短于投资期5。如果将一部分资金投入 σ2—市场收益率的方差; 较长期如8年债券,8年期债券的延续期为5.87,长于投资年数, 一债券j收益率的方差: 将8年期与5年期债券以一定比例配合,达到加权平均的延续期 Pm一债券j和市场收益率的相关系数。 =5年,即可在5年内稳获每年10%的收益。求方程组的解: 在将B系数这一概念应用于有固定收入的债券时要解决 「x+y=100% 以下几个问题: 4.71x+5.87y=5 1.合适的市场收入益率是多少? 式中,x一5年期债券投资比例: 2.个别债券的收益率如何计量? 一8年期比例。 3.随着时间的推移债券的期限会逐渐少,这与股票在理 x=75%,y=25% 论上期限无限是不同的。因此,债券与市场收益率的协方差 5年期债券投入750万元,8年期债券投入250万元即可实现加 不稳定,从而使债券的B系数不稳定。 权平均延续期等于5年的效果。利率下降时,新得利息再投资的收 市场收益率可以采用全部股票的指标,全部债券的指标, 益虽然降低了,但8年期债券的价格攀升可抵偿损失。 或者两者的结合,或持有收益率HPR。而债券期限不断缩短 的问题,是债券自身固有的特性,没有办法解决。正因为如此, 债券投资的B系数(Bond Investment B Coefficient) 计算个别债券的系统性风险时,没有一个稳定的B系数指标。 同股票风险指标一样,债券风险也可用B系数来表示。B 表5-1-11 债券风险指标的比较 样本数目 穆迪级别 平均利息 平均期 平均持 平均最终 由最终收益率 HPR B系数基于 限(年) 续期(年) 收益率 计算的平均σ 最终收益率 12 Aaa 5.38(%) 18.17 13.00 7.97(%) 0.61(%) 0.807 0.744 32 Aa 5.36 17.38 12.9 8.14 0.70 0.805 0.793 74 A 5.67 16.32 12.2 8.63 0.84 0.795 0.896 32 Baa 5.97 17.00 11.8 9.23 0.97 0.782 0.953 12 Ba 6.24 14.50 10.4 10.47 1.23 0.905 1.140 10 B 6.68 17.50 10.1 12.51 1.85 1.460 2.133 172 5.75(%) 16.17 12.1 8.68(%) 0.91% 0.926 0.890 Duvall和Cheney比较了传统风险指标(级别、利息、期限) 下降。组合中的债券数量越多。增加新的债券对降低风险的 和新的风险指标(标准差、持续期和B系数)(见表5-1一 作用越小。 11)。该研究结果是在分析美国1973-1976年172种随机抽 他们的研究结果表明,债券组合中的理想数量是8一16 样的公司债券得到的。所有债券的期限都是长期的,级别从 Aaa-B。从计算出来的到期收益率的总体变动程度来看,低利 率债券的变动性要大些,最后两栏是通过采用从全部172种 10 样本债券构造的总债券指标而估计出来的B系数。B系数的 9 1 第一栏是以PR作为收益指标而计算的B系数:第二栏是采 用到期收益率而计算的B系数。B系数值在Aaa-A级别债券 8 之间是相似的,而在Aaa-B之间存在着较大的差别。 > Aaa 债券组合策略(Bond Combination Tactics) Aa 债券不同于股票,债券的总风险本质上是系统性的。当 利率与收益率变动时,所有债券价格与收益率变化在本质上 是完全相同的。即每一种债券与另一种债券在价格与收益率 Baa 变动方面很少有独立变化。 LLLLLL 12468101418 40 但是Me Enally和Boardman的研究结果表明(如图5-1 -4所示),当债券数量增加时,债券的总风险(方差)明显地 图5-1-4(a)债券种类与风险
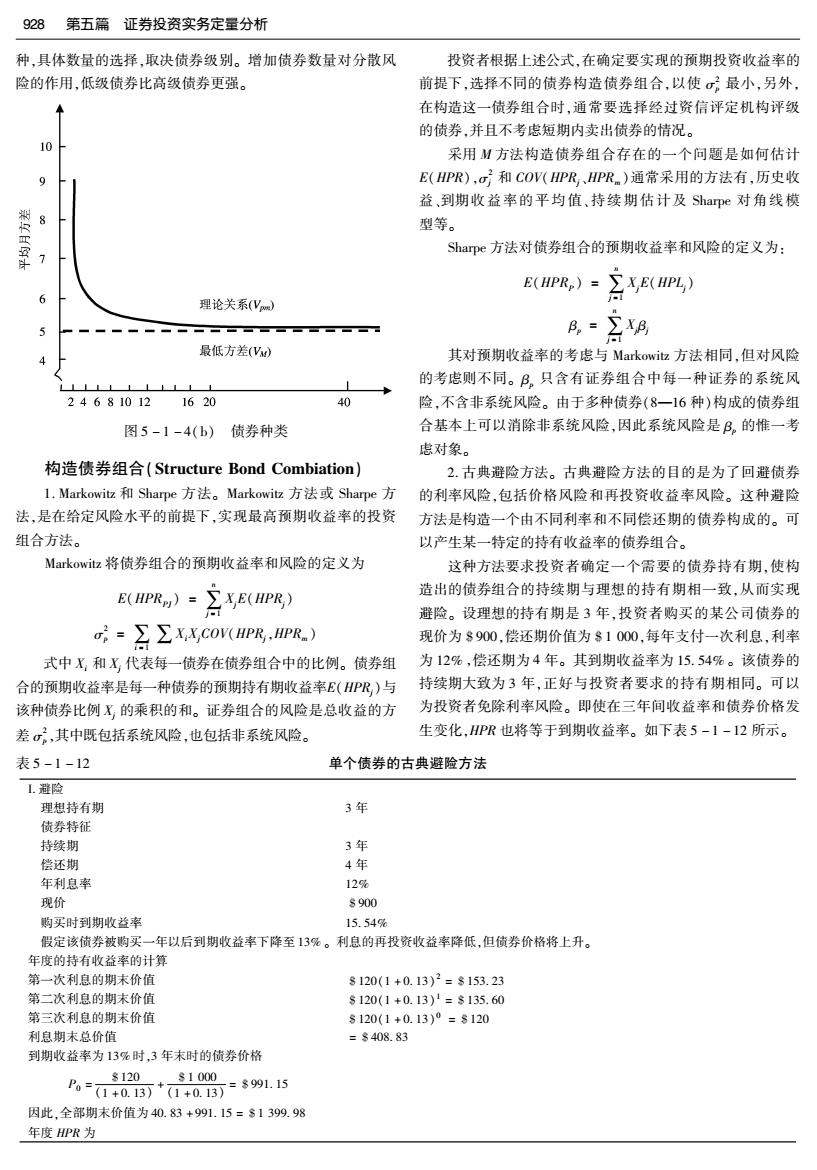
928第五篇证券投资实务定量分析 种,具体数量的选择,取决债券级别。增加债券数量对分散风 投资者根据上述公式,在确定要实现的预期投资收益率的 险的作用,低级债券比高级债券更强。 前提下,选择不同的债券构造债券组合,以使最小,另外, 在构造这一债券组合时,通常要选择经过资信评定机构评级 的债券,并且不考虑短期内卖出债券的情况。 10 采用M方法构造债券组合存在的一个问题是如何估计 E(HPR),G和COV(HPR、HPR.)通常采用的方法有,历史收 益、到期收益率的平均值、持续期估计及Sharpe对角线模 型等。 翠 Sharpe方法对债券组合的预期收益率和风险的定义为: E(HPR)=∑X,E(HPL) 理论关系(V) B,=∑9 最低方差(Vw) 其对预期收益率的考虑与Markowit恤方法相同,但对风险 1上 的考虑则不同。B。只含有证券组合中每一种证券的系统风 246810121620 40 险,不含非系统风险。由于多种债券(8一16种)构成的债券组 图5-1-4(b) 债券种类 合基本上可以消除非系统风险,因此系统风险是B。的惟一考 虑对象。 构造债券组合(Structure Bond Combiation)】 2.古典避险方法。古典避险方法的目的是为了回避债券 l.Markowitz和Sharpe方法。Markowitz方法或Sharpe方 的利率风险,包括价格风险和再投资收益率风险。这种避险 法,是在给定风险水平的前提下,实现最高预期收益率的投资 方法是构造一个由不同利率和不同偿还期的债券构成的。可 组合方法。 以产生某一特定的持有收益率的债券组合。 Markowitz将债券组合的预期收益率和风险的定义为 这种方法要求投资者确定一个需要的债券持有期,使构 E(PR,)-2XE(PR) 造出的债券组合的持续期与理想的持有期相一致,从而实现 避险。设理想的持有期是3年,投资者购买的某公司债券的 =∑XXCo(PR,HPR.) 现价为$900,偿还期价值为$1000,每年支付一次利息,利率 式中X和X代表每一债券在债券组合中的比例。债券组 为12%,偿还期为4年。其到期收益率为15.54%。该债券的 合的预期收益率是每一种债券的预期持有期收益率E(HPR)与 持续期大致为3年,正好与投资者要求的持有期相同。可以 该种债券比例X的乘积的和。证券组合的风险是总收益的方 为投资者免除利率风险。即使在三年间收益率和债券价格发 差,其中既包括系统风险,也包括非系统风险。 生变化,HPR也将等于到期收益率。如下表5-1-12所示。 表5-1-12 单个债券的古典避险方法 1.避险 理想持有期 3年 债券特征 持续期 3年 偿还期 4年 年利息率 12% 现价 8900 购买时到期收益率 15.54% 假定该债券被购买一年以后到期收益率下降至13%。利息的再投资收益率降低,但债券价格将上升。 年度的持有收益率的计算 第一次利息的期末价值 8120(1+0.13)2=$153.23 第二次利息的期末价值 s120(1+0.13)1=$135.60 第三次利息的期末价值 8120(1+0.13)0=$120 利息期末总价值 =$408.83 到期收益率为13%时,3年末时的债券价格 8120 .s1000 P=0+013++03=891.15 因此,全部期末价值为40.83+991.15=$1399.98 年度HPR为

第1章债券投资业务929 续表 81399.98=8900(1+r)3 1.5555=(1+r)3 1.1586=1+r r=15.86% Ⅱ.假定收益率不变时的年度PR的计算 第一次利息的期末价值 $120(1+0.1554)2=8160.19 第二次利息的期末价值 8120(1+0.1554)=$138.65 第三次利息的期末价值 8120(1+0.1554)0=8120 全部利息的期末价值 =$418.84 到期收益率为15.54%时,第三年年底时的债券价格 120 1000 B=0+0.1554+0+0.15554=$969.36 年度HPR为 $418.84+$969.36=900(Hr)3 1.5424=(1+r)3 r=15.54% 表5-1-12的第一部分,是根据13%的到期收益率计算些偏向于被动投资策略,即只保证投资收益维持在一个事先 的三次付息的期末价值。 确定的水平上。有条件免险的组合策略则是主动投资策略与 因为到期收益率在购买债券的一年后从15.54%下降至 被动投资策略的综合。这一组合方式要求投资者确定一个最 13%。同时,由于债券的偿还期为4年,三年后其价格并不是低的收益率(HPR)水平。如果组合的收益水平高于最低标 其面值的$1000,因为票面利率是12%而到期收益率为准,投资者可以进行主动投资管理,追求更高的收益。而一旦 13%。又由于期限存在差别,债券的价值或出卖价格需要计 债券组合的收益水平降到了最低标准线,则采取古典避险方 算出来。这一计算结果意味着在持有期末,投资者将以法,调整债券组合的持续期,使之与要求的持续期相适应,确 $991.15的价格将债券卖出。将各次利息的期末价值与出卖保一定的收益水平。 价格相加,表明投资者的期末总收入为$1399.98,而三年前 的投资额为8900,年度的PR为15.86%,大致与最初的到期 国际投资收益率的计算(International Investment 收益率相等。这一细小的差别是由于债券的持续期不是正好 Yield Rate Calculation) 3年,而是3.37年。 国际投资收益率的计算指在进行国际投资时,汇率的变 应当指出,如果多种债券的收益发生变化,债券组合的持 动可以改变投资者所获得的收益率的计算。 续期将发生变化,偏离理想的持有期,这时,债券组合就不能 图5-1-5显示出了一位美国投资者将100美元投资到 再完全免除利率风险,需要重新调整债券组合,使持续期等于 德国股票市场上,一年后再收回投资的全过程。 剩余的持有期。债券组合的持续期为: 美国 第一步 德国 D,=0 1=0$100 a($/DM0=0.6 166.67DM 式中,X一债券j在债券投资组合中的资金比率: D一债券的持续期。 R=15% 第二步 如果债券组合的持续期等于其理想的持有期,该债券组 第三步 合就可以免除利率风险。 t=nS95.8 191.67DM 这里所讨论的持续期指标被称为古典模型或单因素模 fa($/DM0=0.6 型。当用这一模型免除债券组合风险时,一般都假设利率期 图5-1-5一位美国投资者在德国股票 限结构是平滑的,平行移动的。这就要求投资者必须适时调 市场上所获得的收益 整债券组合以适应收益率、价格及偿还期的变化。即始终保 持债券组合的持续期等于投资期。如果投资者最初的投资期 第一步,将美元($)兑换成德国马克(DM)。假设当天的 为5年,最开始的债券组合的持续期也应该是5年。一年之 美元汇率是($/DM)=0.6。也就是说,1德国马克可以兑 后,剩余的投资期为4年,债券组合也应调整、修改以使其持 换0.6美元,或者,1美元可兑换1.67德国马克,即f。(8/ 续期为4年。 3.有条件免险。按照古典避险方法构造债券组合多少有 DM)=1/0.6=1.67。所以,100美元可以兑换成166.67 马克
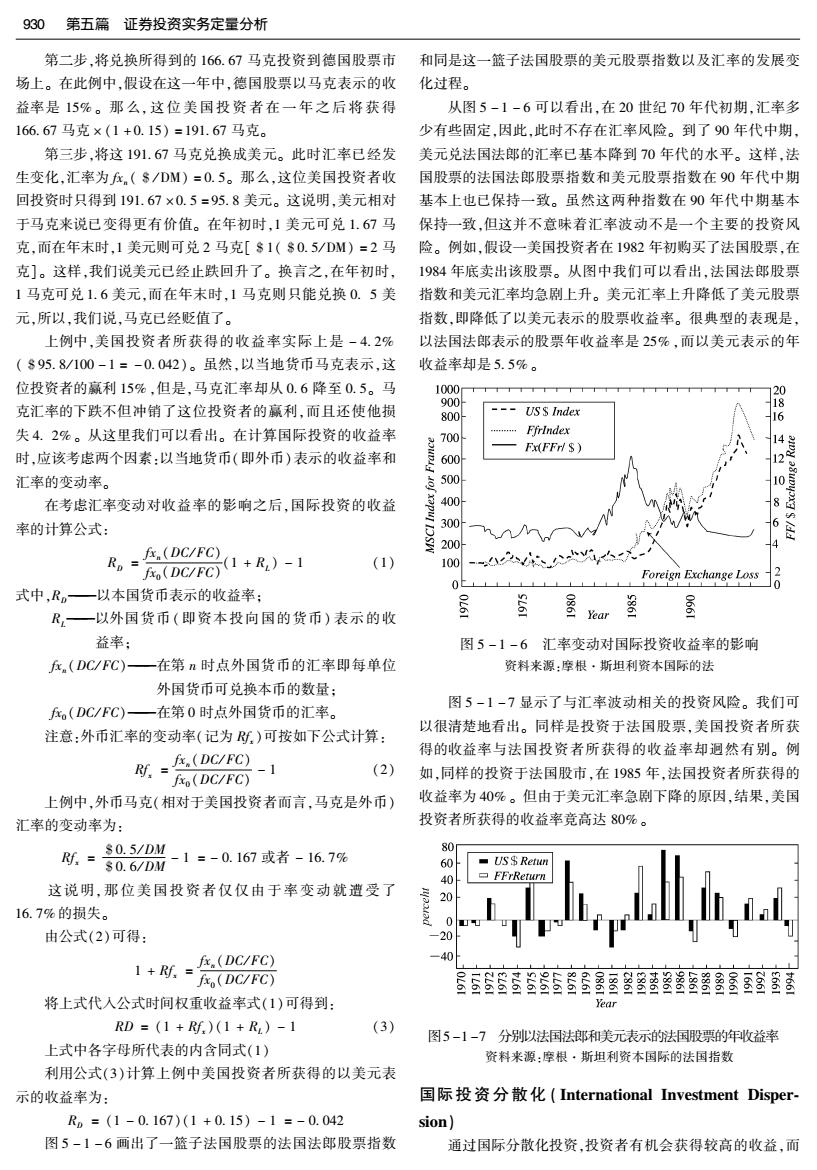
930第五篇证券投资实务定量分析 第二步,将兑换所得到的166.67马克投资到德国股票市 和同是这一篮子法国股票的美元股票指数以及汇率的发展变 场上。在此例中,假设在这一年中,德国股票以马克表示的收 化过程。 益率是15%。那么,这位美国投资者在一年之后将获得 从图5-1-6可以看出,在20世纪70年代初期,汇率多 166.67马克×(1+0.15)=191.67马克。 少有些固定,因此,此时不存在汇率风险。到了90年代中期, 第三步,将这191.67马克兑换成美元。此时汇率已经发 美元兑法国法郎的汇率已基本降到70年代的水平。这样,法 生变化,汇率为f.($/DM)=0.5。那么,这位美国投资者收国股票的法国法郎股票指数和美元股票指数在90年代中期 回投资时只得到191.67×0.5=95.8美元。这说明,美元相对基本上也已保持一致。虽然这两种指数在90年代中期基本 于马克来说已变得更有价值。在年初时,1美元可兑1.67马保持一致,但这并不意味着汇率波动不是一个主要的投资风 克,而在年末时,1美元则可兑2马克[$1($0.5/DM)=2马险。例如,假设一美国投资者在1982年初购买了法国股票,在 克]。这样,我们说美元已经止跌回升了。换言之,在年初时,1984年底卖出该股票。从图中我们可以看出,法国法郎股票 1马克可兑1.6美元,而在年末时,1马克则只能兑换0.5美指数和美元汇率均急剧上升。美元汇率上升降低了美元股票 元,所以,我们说,马克已经贬值了。 指数,即降低了以美元表示的股票收益率。很典型的表现是, 上例中,美国投资者所获得的收益率实际上是-4.2% 以法国法郎表示的股票年收益率是25%,而以美元表示的年 (895.8/100-1=-0.042)。虽然,以当地货币马克表示,这 收益率却是5.5%。 位投资者的赢利15%,但是,马克汇率却从0.6降至0.5。马 120 克汇率的下跌不但冲销了这位投资者的赢利,而且还使他损 900 18 800H USS Index 16 失4.2%。从这里我们可以看出。在计算国际投资的收益率 FfrIndex 700 Fx(FFriS) 时,应该考虑两个因素:以当地货币(即外币)表示的收益率和 600 汇率的变动率。 500 在考虑汇率变动对收益率的影响之后,国际投资的收益 率的计算公式: 300 6 d R-81+成)-1 200 (1) 100 Foreign Exchange Loss 式中,R。一以本国货币表示的收益率: R,一以外国货币(即资本投向国的货币)表示的收 2061 066 益率: 图5-1-6汇率变动对国际投资收益率的影响 在.(DC/FC)一在第n时点外国货币的汇率即每单位 资料来源:摩根·斯坦利资本国际的法 外国货币可兑换本币的数量: 图5-1-7显示了与汇率波动相关的投资风险。我们可 f。(DC/FC)一在第0时点外国货币的汇率。 以很清楚地看出。同样是投资于法国股票,美国投资者所获 注意:外币汇率的变动率(记为:)可按如下公式计算: (DC/FC) 得的收益率与法国投资者所获得的收益率却迥然有别。例 Ry, f(DC/FC) -1 (2) 如,同样的投资于法国股市,在1985年,法国投资者所获得的 上例中,外币马克(相对于美国投资者而言,马克是外币) 收益率为40%。但由于美元汇率急剧下降的原因,结果,美国 汇率的变动率为: 投资者所获得的收益率竞高达80%。 Rf.0.6/DM $0.5/DM -1=-0.167或者-16.7% ■US$Ret 40 FFrReturn 这说明,那位美国投资者仅仅由于率变动就遭受了 16.7%的损失。 由公式(2)可得: -20 1+f =(DC/FC) -40 fo(DC/FC) 将上式代人公式时间权重收益率式(1)可得到: Year RD=(1+Rf.)(1+R)-1 (3) 图5-1-7分别以法国法郎和美元表示的法国股票的年收益率 上式中各字母所代表的内含同式(1) 资料来源:摩根·斯坦利资本国际的法国指数 利用公式(3)计算上例中美国投资者所获得的以美元表 示的收益率为: 国际投资分散化(International Investment Disper- R,=(1-0.167)(1+0.15)-1=-0.042 sion】 图5-1-6画出了一篮子法国股票的法国法郎股票指数 通过国际分散化投资,投资者有机会获得较高的收益,而