
第1章债券投资业务 921 N。一投资者在第i期期初所拥有的证券的数量: 到债券出售日这一段时间的应得利息。同时,该债券的购买 P。一在第n期期末证券的市场价格: 者,到下次利息支付日前不管何日购进均能领到半年的利息。 R。一在第i期期初证券的市场价格: 为了解决这个矛盾,在买卖债券时,买者向卖者除支付债券价 T—所得税税率: 格以外,还应该支付从上次利息支付日到债券出售日这段时 T一资本增益税税率。 期的利息,这一段时期的利息也就是应得利息或称为应计利 等式右边的一-N.(P。-P。)T项表示由于资本增益税 息(accraedinterest)。应计利息计算法是在计算利息收入时以 而减少的收益(或表示由于资本增益而被扣除的税收)。不 应计利息为基础,而不应以现金收入为基础。计算证券的收 过,这只是一个近似值,因为该式忽略了由于对收益进行再投 益率时应充分考虑各种应得到利息或股息。由于股票股息包 资而发生的资本增益税。 含在股票的交易价格中,故计算股票收益率时可以以交易价 下面举一个例子来说明税后收益率的计算方法。 格为标准:而债券的交易价格中并不包含应得利息,故计算债 假设你在1月1日买进股票,在当年的12月31日卖出股 券的收益率时应考虑债券的应得利息(或应计利息)。 票。参见表5-1-6中的数据。第一时期的期间收益率(考 在计算债券的收益时,我们解决应计利息的方法是,将期 虑税收)是: 初的应计利息和期末的应计利息分别加到期初的价格和期末 [(880-$100+$2×(1-0.25))/8100=-0.1850 的价格上去。这样,债券收益率的计算表达则为: 可见,这个税后的期间收益率要比在没有考虑税收时的 R=P+)-(P+A)+C] 期间收益率-0.18低。注意:税收同样也降低于时间权重收 (P1+AL1) 益率。税前的时间权重收益率是8.42%,而税后的时间权重 式中,R一债券在第i期的期间收益率; 收益率则降至6.27%。另外,在本例中,由于购入价和卖出价 P一债券在第i期期末的市场价格: 是一致的(均为100美元每股),故没有资本增益税发生。 P.1一债券在第i-1期期末的市场价格: 表5-1-6计算ABC公司股票税后的时间权重收益率。 A1一在第i期期末时债券中的应计利息(如果你出售 假设收入税税率和资本增益税税率均为25% 债券,你将得到这部分应计利息): A山1一在第i-1期期末时债券上积累的应计利息(如 日期 第i期 现金 市场 税后期间 税后时间权 股息 价格 收益率 重收益率 果你购进该债券,你则必须支付这部分应计利 1月1日 8100 息): 2月15日 1 $2 s80 -0.1850 -0.1850 C:一债券发行者在第i期内按债券规定的日期和利率 5月15日 2 $2 895 0.2063 -0.0169 支付给债券持有者的息票利息。 8月15日 3 82 8105 0.1211 0.1022 这种息票利息一般只在固定的日期(即债券上规定的日 11月15日4 $2 8120 0.1571 0.2753 12月31日 5 8100 -0.1667 0.0627 期)支付,其余时间不支付,且如果发行者在支付息票利息之 后,那么积累在债券上的应计利息便为零。关于这一点可以 我们也可以用下列等式来估算税后收益率: 参见表5-1-5的有关数据。 RAr Bur(1 -T) (3) 表5-1-7(a)具体给出了用综合法计算债券的时间权重 式中,R一税后收益率; 收益率(考虑应计利息)的解题过程。该表列出了各个日期的 Rr一税前的时间权重收益率: 债券市场价格、债券发行者支付的息票利息以及应计利息。 T—收入税税率。 由期间收益率式(1)可知,在计算期间收益率时应先计算期初 当然,这里还应假定:(1)所有收入税都在各个时期的期 和期末证券的市场价值,在这里债券的市场价值应等于债券 末支付:(2)收人税税率与资本增益税税率相同。 的市场价格加上积累在债券上的应计利息。例如,计算第1 运用估算式(3),我们可以得出税后的时间权重收益 期(从1月1日到5月15日)的期间收益率时,期初市场价值 率为: 等于期初市场价格加上应计利息,即期初市场价值为$990+ Rr=0.0842×(1-0.25)=0.0632 810=81000:期末市场价值则是81040+810=$1040: 这个结果与0.0627之间只存在5个基本点的误差。但 在第i期的期间收人为投资者在5月15日收到的息票利息, 是,当第期期末的市场价格和第1期期初的市场价格相差很 即为40美元。期中,上述的10美元应计利息可通过如下式子 大,且存在资本增益税发生时,那么,这个误差便会很大。 得出:(1.5个月/6个月)×$40=$10。这里的1.5个月是 指从头一年11月15日到下一年的1月1日,所以,第一期的 应计利息的债券收益率(Interest Accrued Liability 期间收益率是: rield Rate) R=【81040-(890+810)+$40]=0.08或89% 传统的计算债券的收益率的方法,一般都是按固定日期 8990+810 每年支付两次利息,其他日期并不支付利息。这样凡是在付 在债券发行人支付利息之后,积累在债券上的应计利息 息日以前出售债券的投资者,就失掉了从上一次利息支付日 便为零了。即所有的应计利息都已由发行人在约定日期(如
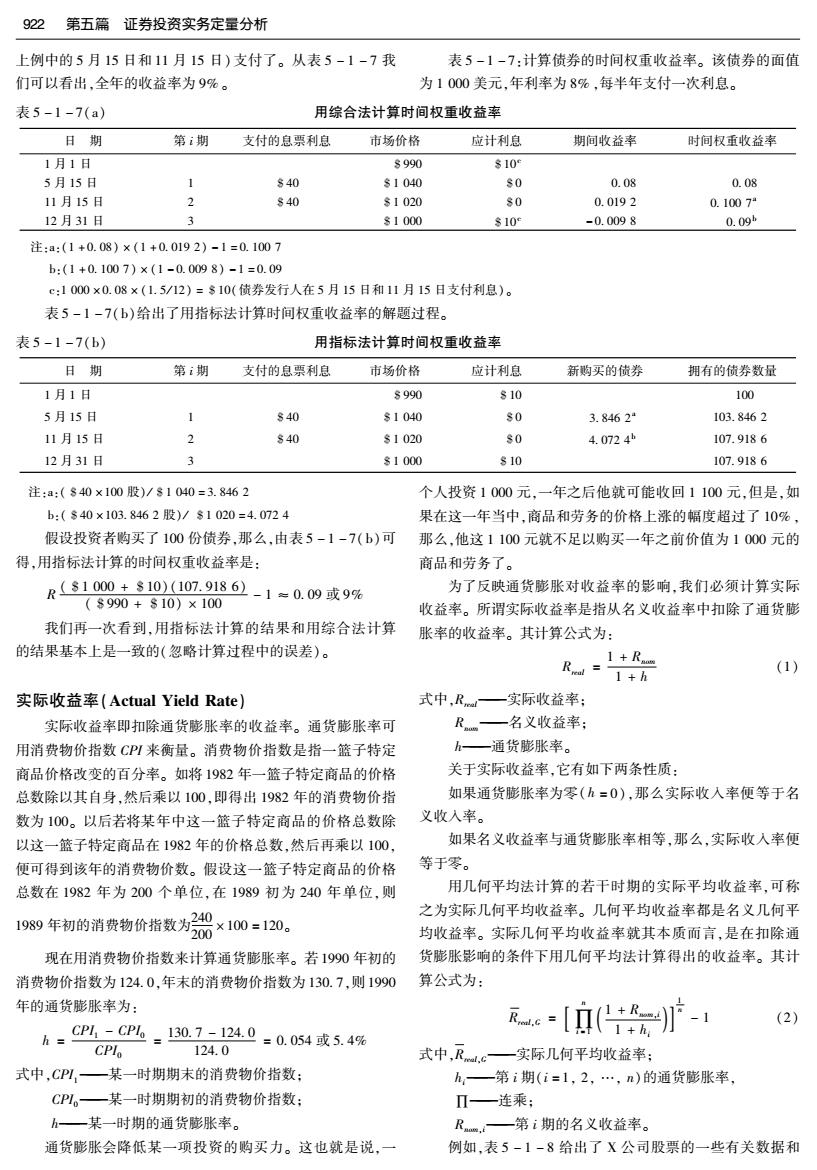
922 第五篇证券投资实务定量分析 上例中的5月15日和11月15日)支付了。从表5-1-7我 表5-1-7:计算债券的时间权重收益率。该债券的面值 们可以看出,全年的收益率为9%。 为1000美元,年利率为8%,每半年支付一次利息。 表5-1-7(a) 用综合法计算时间权重收益率 日期 第i期 支付的息票利息 市场价格 应计利息 期间收益率 时间权重收益率 1月1日 8990 8109 5月15日 1 s40 s1040 s0 0.08 0.08 11月15日 2 840 $1020 80 0.0192 0.1007 12月31日 81000 810 -0.0098 0.09b 注:a:(1+0.08)×(1+0.0192)-1=0.1007 b:(1+0.1007)×(1-0.0098)-1=0.09 c:1000×0.08×(1.5/12)=$10(债券发行人在5月15日和11月15日支付利息)。 表5-1-7(b)给出了用指标法计算时间权重收益率的解题过程。 表5-1-7(b) 用指标法计算时间权重收益率 日期 第i期 支付的息票利息 市场价格 应计利息 新购买的债券 拥有的债券数量 1月1日 s990 810 100 5月15日 1 s40 s1040 s0 3.8462 103.8462 11月15日 840 $1020 S0 4.0724b 107.9186 12月31日 3 81000 810 107.9186 注:a:(840×100股)/81040=3.8462 个人投资1000元,一年之后他就可能收回1100元,但是,如 b:($40×103.8462股)/81020=4.0724 果在这一年当中,商品和劳务的价格上涨的幅度超过了10%, 假设投资者购买了100份债券,那么,由表5-1-7(b)可 那么,他这1100元就不足以购买一年之前价值为1000元的 得,用指标法计算的时间权重收益率是: 商品和劳务了。 Rs1000+$10)107.9186)-1=0.09或9% 为了反映通货膨胀对收益率的影响,我们必须计算实际 ($990+$10)×100 收益率。所谓实际收益率是指从名义收益率中扣除了通货膨 我们再一次看到,用指标法计算的结果和用综合法计算 胀率的收益率。其计算公式为: 的结果基本上是一致的(忽略计算过程中的误差)。 1+R Rl=1+h (1) 实际收益率(Actual Yield Rate) 式中,R一实际收益率; 实际收益率即扣除通货膨胀率的收益率。通货膨胀率可 R一名义收益率; 用消费物价指数CPI来衡量。消费物价指数是指一篮子特定 h—通货膨胀率。 商品价格改变的百分率。如将1982年一篮子特定商品的价格 关于实际收益率,它有如下两条性质: 总数除以其自身,然后乘以100,即得出1982年的消费物价指 如果通货膨胀率为零(h=0),那么实际收入率便等于名 数为100。以后若将某年中这一篮子特定商品的价格总数除 义收入率。 以这一篮子特定商品在1982年的价格总数,然后再乘以100, 如果名义收益率与通货膨胀率相等,那么,实际收入率便 便可得到该年的消费物价数。假设这一篮子特定商品的价格 等于零。 总数在1982年为200个单位,在1989初为240年单位,则 用几何平均法计算的若干时期的实际平均收益率,可称 1989年初的消费物价指数为0×100=120。 之为实际几何平均收益率。几何平均收益率都是名义几何平 均收益率。实际几何平均收益率就其本质而言,是在扣除通 现在用消费物价指数来计算通货膨胀率。若1990年初的 货膨胀影响的条件下用几何平均法计算得出的收益率。其计 消费物价指数为124.0,年末的消费物价指数为130.7,则1990 算公式为: 年的通货膨胀率为: (2) h=CPCP4=130.7-124.0=0.054或5.4% CPlo 124.0 式中,Rl.c一实际几何平均收益率: 式中,CPI,一某一时期期末的消费物价指数: h,一第i期(i=1,2,…,n)的通货膨胀率, CPL。一某一时期期初的消费物价指数: Π一连乘: h一某一时期的通货膨胀率。 R—第i期的名义收益率。 通货膨胀会降低某一项投资的购买力。这也就是说,一 例如,表5-1-8给出了X公司股票的一些有关数据和

第1章债券投资业务 923 相应时期的通货膨胀率。则X公司股票在这五个时期中的实 债券流动性风险亦称债券变现风险,指的是债券不能以 际几何平均收益率为: 合理的价格及时出让的风险。对于准备将债券持有到期的投 R4.c=[(1+0.10)(1+0.08)(1+0.32)(1- 资者来说,流动性风险不重要。 0.12)(1+0.06)/(1+0.02)(1+0.04)(1+ 0.06)(1+0.05)(1+0.12)]-1 债券回购风险(Call Risk) =(1.4628/1.3224)方-1 某些债券的发行条款可能允许发行者在债券到期日之前 赎回部分或全部债券(即提前偿还),这实际上是给发行者提 =0.0204或者2.04% 供了一种选择权。如果在未来某个时间市场收益率低于债券 发行时的市场收益率很多时,发行者将按既定价格赎回债券 表5-1-8 X公司股票在各个时期的名义收益率 并以较低的利率发行新债券来替代它。 和相应各个时期的通货膨胀率 从债券投资者的角度来看,回购条款有三个不利之处: 必 各个时期的名义收益率R,d 通货膨胀率h, 1.现金流具有不确定性: 10% 2% 2.因为发行者在市场利率下降时可能赎回债券,投资者 3 8% 4% 面临较大的再投资风险: 32% 6% 3.可回购债券的增值潜力有限。通常,利率下降时,债券 -12% 5% 6% 12% 价格上升。但对于可赎回债券而言,其价格上升将以既定的 赎回价格为上限。 认购者收益率(Subscribers'Yield Rate) 债券的外汇风险(Currency Risk) 认购者收益率是债券的发行条件之一,也是投资者判断 投资者购买外币债券时,其投资收益受外汇汇率的影响。 某一债券与其他债券相比是否有吸引力的标准,同时还是认 这种由于外汇汇率波动而导致的风险称为债券的外汇风险。 购者所得的偿还价格和发行价格的差额利润率及票面利息率 购买本币债券不存在外汇风险。 的总和。投资者在购买债券之前就把收益率与银行存款利息 和股份投资的收益率比较,从而判断向哪方面投资更为有利。 债券再投资收益率风险(Bond Reinvestment Yield 认购者收益率的计算公式为: Rate Risk)】 认购者收益率= 如果运用债券利息收入进行再投资,由于再投资收益率 /面额×票面利率+票面价格一发行价格Y发行价格 偿还期限 的不确定性,再投资是有风险的。到期收益率的确定要求利 例如,某投资者以900元的市场价格买进一张面值为 息收入按照与到期收益率相同的再投资收益率进行再投资。 1000元,年利10%,期限10年的债券。其收益率的计算如下: 投资者利用其他诸如预期持有收益率E(HPR)等收益指标来 1000×10%+1000-900 决定持有期时,也必须解决再投资风险问题。 收益率 10 —=12.22% 假设一投资者要在下面两种债券中作出选择:A债券期 900 限2年,利率为8%,B债券利率为12%,期限为4年。两种债 其实际收益率超过其名义收益率2.22%。 券的资信级别均为Aa,每年付利息一次。首先,假设在两年的 持有期内到期收益率保持稳定。则如表5-1-9第一部分所 债券投资的利率风险(nterest Rate Risk)】 列的那样,如果投资者购买债券A,到第二年年底时,现金流动 债券投资的利率风险指的是,由于市场利率波动带来的 量总值为$1168.80,其中包括第一年80元利息以11%投资 债券投资收益的不确定性。通常,债券价格与市场利率反方 收益率进行再投资,到第二年年底时得到的88.80$,以及第 向变化:当市场利率上升时,债券价格下跌:市场利率下降时, 二年年底时的利息和本金收入80元和1000元。11%的年持 债券价格上升。如果债券价格上升,投资者将获得资本收益: 有收益率(HPR)与原始的到期收益率相同。关于债券B,假设 相反,债券价格下跌,投资者将蒙受损失。 第二年年底以市场价格出卖,由于到期收益率等于利息率,并 且稳定不变,债券的价格也不变,其年持有收益率等于到期收 债券违约风险(Default Risk) 益率12%。投资者通过比较这一结果,并且认定收益率实际 债券违约风险又称债券信用风险,指的是债券发行人在 上稳定不变,他将毫不迟疑地选择B债券,原因是B债券的持 规定的时间不能及时支付利息或偿还本金从而使投资者蒙受 有收益率(HPR)高。 损失的风险。 表5-1-9第二部分假设现金流量以8%的收益率作再 投资,这使得A债券的年持有收益率降至10.89%。同时应当 债券流动性风险(Liquidity Risk) 指出,由于投资者一直持有A债券至偿还期,他不能得到因收

924第五篇证券投资实务定量分析 益率下降带来的价格上升的好处。对于B债券,再投资收益 债券就会较有吸引力了。B债券价格将下跌,并且冲销了再投 的下降的损失完全被因到期收益率降至8%而引起价格上升 资的收益。表5-1-9的第三部分说明了这一点。 的资本利得所抵消。B债券的HPR为14.93%,高于12%的 如果持有期延长至两年以上,同时再投资收益率上升,A 到期收益率。 债券就更有吸引力了。因为两年后1000$的本金收入可以 若现金流量能以更高的收益率去再投资,则在上例中,A从事再投资。 表5-1-9 再投资收益率风险 L当利息按最终收益率从事再投资时(最终收益率稳定不变) 债券A 债券B 目前到期收益率 11% 12% 市场价格 $948.62 s1000 假定持有期为两年,到第二年年底时的现金流量总值 第一年利息 80×(1·11)=888.80 120×(1·12)=多134.40 第二年利息 80×(1·0)=s80.00 120×(1·0)=8120.00 偿还价格 8=1000.00 、 第二年底价格 8=1000.00 第二年年底总值 $=1168.80 8=1254.40 年持有收益率HPR: 债券A:81168.80=8948.62(1+r)2 1.2321=(1+r)2 1+r=个.232T r=11% 债券B:$1254.40=$1000(1+r)2 1.2544=(1+r)2 r=12% Ⅱ.计算当利息的再投资收益率低于一般到期收益率时的HPR 债券A 债券B 假设的再投资收益率: 8% 8% 第二年年底的总现金流量: $1166.40 81320.93 HPR: 10.89% 14.93% Ⅲ.计算如果再投资收益率高于一般到期收益率时的HPR 债券A 债券B 假设的再投资收益率: 14% 14% 第二年年底的总现金流量: $1171.20 81223.86 HPR: 11.11% 10.63% 投资者必须从利息所得和偿还价格两方面考虑再投资收 率,和通货膨胀率1。,那么,简单算法: 益率的风险。从表5-1-9中,可以得到以下基本结论: r。=,+ 1.如果再投资收益率不等于到期收益率,持有期收益率 如果,为12%,通货膨胀率为7%,实际收益率为5%。 HPR将不等于到期收益率。 精确算法为: 2.即使债券的偿还期与投资者的理想持有期相同,如果 (1+r.)=(1+,)(1+1)》 在此间内的收益率发生变化,PR与到期收益率依然不相等。 3.未来较高的再投资收益率使得利息率上升,因而期限 1+-1 ,=1+1, 较短的债券更具吸引力。 实际收益率为4.7%。 4.如果收益率下降,再投资收益率将下降,利率较低,期 如果市场不能准确地预期通货膨胀,则债券的名义收益 限较长的债券的价格将大幅上涨,这一资本利得将抵消再投 率就不能正确地体现投资者所要求的实际收益率。如果实际 资收益率下降给投资者带来的损失。 通货膨胀率低于预期通货膨胀率,则实际收益率高于预期的 实际收益率。如果实际通货膨胀率高于预期通货膨胀率,则 债券投资的购买力风险(Purchasing Power Risk) 实际收益率低于预期的实际收益率。这种因通货膨胀导致的 收益率有实际收益率和名义收益率之分。实际收益率是 实际收益率的不确定性,就是购买力风险。 排除通货膨胀影响后的收益率。名义收益率「。包括实际收益

第1章债券投资业务 925 债券系统风险分析指标(Bond System Risk Analysis 有 Index) IC. NMx d五 (2) 1.总风险。债券总风险指标是收益指标的标准差。收益指标 包括直接收益率,到期收益率或持有期收益率HPR等。这一风险指 显然蛋<0 标包括全部收益的总波动,既包括系统风险,也包括非系统风险。 因此,债券价格与市场收益率呈相反方向变化。那么,什 2.持续期。由于大多数债券是定期得到利息收入的,因 么样的债券的价格变化幅度会更大一些呢? 此,投资者在债券到期之前就可得到利息收益。债券的持续 期是债券各期现金流加权平均年份,权数是每一现金流的现 由于号=智x× 值在总现金流现值的比例,计算出来的加权平均的期限就是 有 “持续期”。持续期的定义及计算公式: NM Σ+ D=女(1+订+1+ ∑G+M, -×di (3) M (1) C 2(1+i)(1+i) 名(1++1+) 式中,D—持续期; D= 总" t—现金流入的时期t=1,…,W; Σ4*a MN W一债券的期限或者至到期日的剩余时间: C—t期的利息: 则 一最终收益率: 咒=D dP (4) M一债券的到期日价格。 因此,持续期D反映了市场利率每变化一个百分比,债券 公式(1)的分母是债券的现值。分子与分母很相似,但C, 价格波动多少个百分比。持续期相当于债券价格波动相对于 被乘以t,t=1,…,N,Mw被乘以N。 市场利率波动的倍数。 C M 因为P= 名(1+)+(1+) 如持续期的计算表5-1-10。 表5-1-10 持续期的计算 假设一种债券的最终收益率为14%,面值为10008,年息9%,至偿还期还有5年 【.持续期计算的格式 最终收益率为14% 每一现金流现值占 年 现金流 现金流的现值 的现金系数 总现金流现值的比率 (1) (2) (3) (4) (5) 1 90 0.8772 s78.95 0.0953 2 90 0.7695 69.25 0.0836 90 0.6750 60.75 0.0733 90 0.5921 53.29 0.0643 1090 0.5194 566.15 0.6835 8828.39 1.0000 权数乘以时间阶段的和[(1)×(5)] 0.0953 0.1672 0.2199 0.2572 +3.4175 =4.1571 持续期等于4.1571年 Ⅱ.利用公式(1),直接计算: 1(890) 2($90) +3(890) 4(s90),5(s1090) D=1+0.14)1+0.14京+0+0.14+1+0.14++0.14 $90 890 890 890 s1090 (1+0.14)+(1+0.14)+(1+0.14)+(1+0.14)+(1+0.14) D=$3443.60 =4.157年 8828.39