
·可能的本征值取 L.=mh m=-,-l+1,.,l-1,1称为磁量子数。 L=0,±h,士2h,.,±1h 角动量在空间的取向也是量子化的。 对于一定的角量子数1,磁量子数m可取(2l+1)个值, 角动量在空间z方向的取向只有(21+1)种可能
z = mL h m=-l,-l+1,…,l-1,l 称为磁量子数。 • L ˆ z可能的本征值取 角动量在空间的取向也是量子化的。 Lz = ± ± , ,...2 , ,0 ± lhhh 对于一定的角量子数l ,磁量子数 m 可取(2 l +1)个值, 角动量在空间 z 方向的取向只有(2 l +1)种可能
2.角动量空间量子化的经典矢量模型 L:t 1i=√11+1)h=V6方 L,=2h 0 L.=2h -2h 将角动量想象为一长度为L=V(1+1)h的经典矢量 该矢量在L,轴上的投影在-1h到h之间。 但对矢量的具体方位p不能限制,可以在半顶角α的 圆锥面上的任意方位(其中a=m/V(1+1)),若L, 取定值,则完全不确定
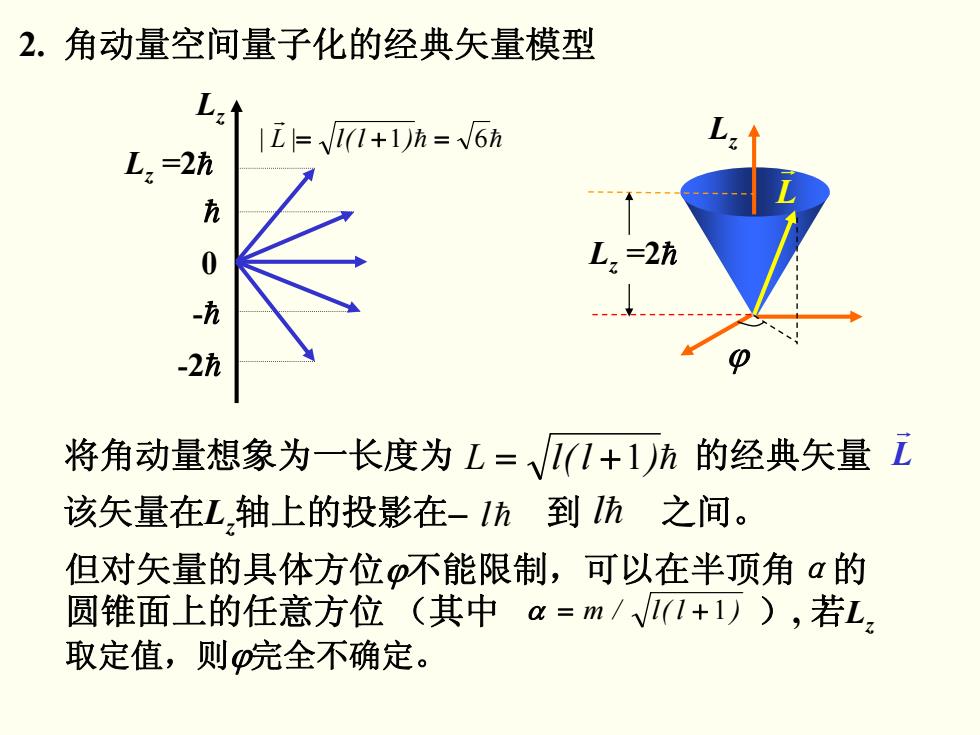
2. 角动量空间量子化的经典矢量模型 该矢量在Lz轴上的投影在 到 之间。 − lh lh 但对矢量的具体方位ϕ不能限制,可以在半顶角α的 圆锥面上的任意方位 (其中 ), 若Lz 取定值,则ϕ完全不确定。 α = + 1 )l(l/m hh r )l(l|L| =+= 61 0 -2h h Lz =2h -h Lz 将角动量想象为一长度为 += 1)l(lL h 的经典矢量 Lr Lz Lz =2h ϕ L r