
第二章方差分析方法 方差分析的数学模型的几条假定: (1)X=u+a;+e i=1,2,,p j=1,2,…,r (22a,=0 cmese,uestc (3)是相互独立且遵从正态分布N(,o) 由这三条建立的模型叫做线性模型。 建立数学模型后,统计分析需要解决两个问题: (1)参数估计 (2)统计检验 School of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 i p i i=1 ij X a 1,2,......, j 1,2,......,r 2 a 0 3 N ij ij i p = + + = = = 2 方差分析的数学模型的几条假定: (1) ( ) ( ) 是相互独立且遵从正态分布 ( , ) 由这三条建立的模型叫做线性模型。 建立数学模型后,统计分析 (1)参数估 需要解决两个 计 (2 问题: )统计检验

第二章方差分析方法 2、参数估计 参数估计即通过子样(样本,一组试验数据)算出统计量, 用这些统计量u和{a},它们的估计量用u和a表示。 根据子样平均值的定义 cmese.uestc 之,u+a+)=4+g+e (2-1-5) …克-,20-a+)a19 (2-1-6) 成空车空 (2-1-7) i= i-1 School of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 2、参数估计 i _ 1 1 _ 1 1 1 1 1 1 a 1 1 ( ) (2 1 5) 1 1 ( ) (2 1 6) 1 1 r r ij i ij i i j j p p r r ij i ij i j i j r p ij j i x a a r r x a p r p r r p r = = = = = = = = = = + + = + + − − = = + + = + − − • • = = • i _ i _ _ _ i 参数估计即通过子样(样本,一组试验数据)算出统计量, 用这些统计量 和{a },它们的估计量用 和 表示。 根据子样平均值的定义 x x 式中: 1 (2 1 7) r ij j= − −

第二章方差分析方法 x是的一个无偏估计量,记作山=x (2-1-8) a的无偏估计是x-x, 即a,=x,-x (2-1-9) cmese,uestc 于是(2-1-3)可以改写为:x,=+a,+ (2-1-10) 式中:1反映了误差 根据(2-1-10)对试验数据进行分解,通过数据的分解可看出 水平效应和误差大小。 试验设计的关键:是把水平效应和实验误差分开,估计它们的值,并进行显著 性检验。 School of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 _ _ _ _ _ i _ 2 1 8 (2 1 9) (2 1 10) a i ij i i i ij x x x l x a x x a l = = − − − = + + − − − ij 记作 ( -- ) 即 于是(2-1-3)可以改写为: x 式中: 根据(2-1-10)对试验数据进行分解 是 的一个无偏估计量, 的无偏估计是 , 反映 ,通过数据的分解可看出 水平效应和误 了误差 差大小。 试验设计的关键:是把水平效应和实验误差分开,估计它们的值,并进行显著 性检验
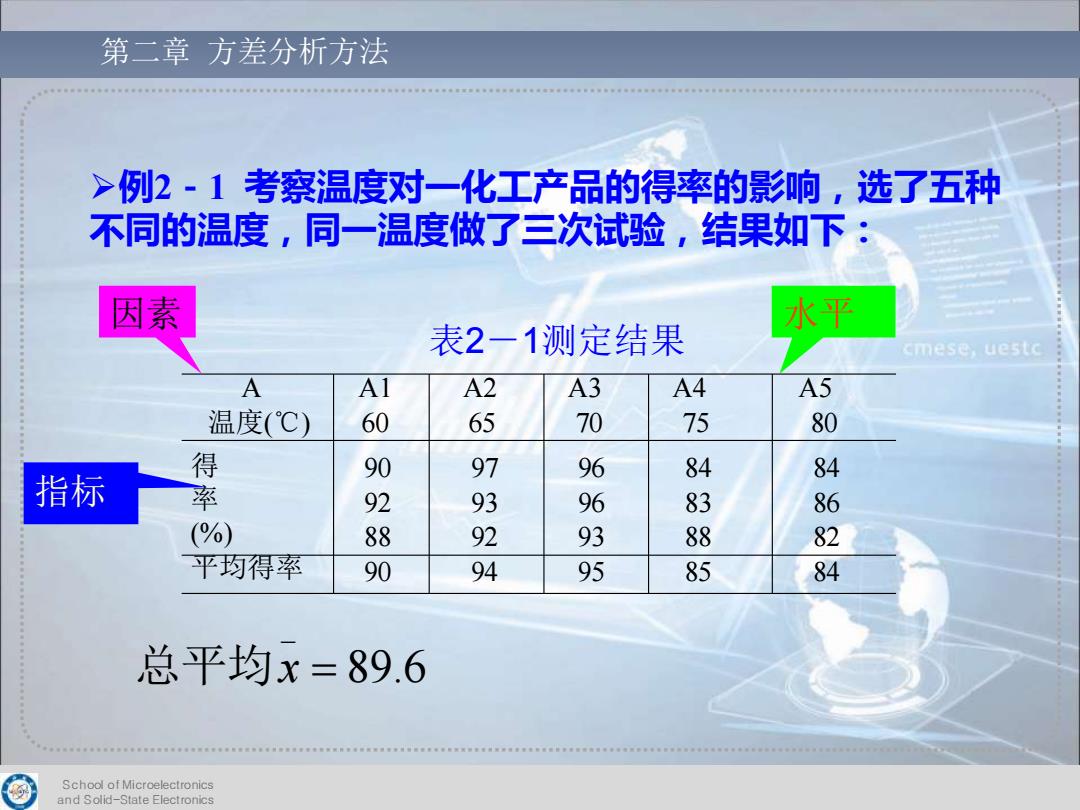
第二章方差分析方法 >例2-1考察温度对一化工产品的得率的影响,选了五种 不同的温度,同一温度做了三次试验,结果如下: 因素 水平 表2一1测定结果 cmese.uestc A Al A2 A3 A4 A5 温度(℃) 60 65 70 75 80 得 90 97 96 84 84 指标 92 93 96 83 86 (%) 88 92 93 88 82 平均得率 90 94 95 85 84 总平均x=89.6 Schodl of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 ➢例2-1 考察温度对一化工产品的得率的影响,选了五种 不同的温度,同一温度做了三次试验,结果如下: A A1 A2 A3 A4 A5 温度(℃) 60 65 70 75 80 得 率 (%) 平均得率 90 97 96 84 84 92 93 96 83 86 88 92 93 88 82 90 94 95 85 84 表2-1测定结果 _ 总平均x = 89.6 因素 水平 指标

第二章方差分析方法 总平均x=89.6 依(2-1-10)式有: 4=x=89.6 11=x1-4-41=90-89.6-0.4=0 41=x1-x=90-89.6=0.4 12=x2-4-41=92-89.6-0.4=2 uestc a2=x2-x=94-89.6=4.4 13=x3-4-41=88-89.6-0.4=-2 43=x3-x=95-89.6=5.4 这样x,就可以分解成三个数之和: x11=89.6+0.4+0 a4=x4-x=85-89.6=-4.6 x12=89.6+0.4+2 45=x-x=84-89.6=-5.6 X13=89.6+0.4-2 School of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 _ _ _ _ 1 1 _ _ 2 2 _ _ 3 3 _ _ 4 4 _ _ 5 5 89.6 89.6 90 89.6 0.4 94 89.6 4.4 95 89.6 5.4 85 89.6 4.6 84 89.6 5.6 x x a x x a x x a x x a x x a x x = = = = − = − = = − = − = = − = − = = − = − = − = − = − = − 总平均 11 11 1 12 12 1 13 13 1 90 89.6 0.4 0 92 89.6 0.4 2 88 89.6 0.4 2 89.6 0.4 0 89.6 0.4 2 89.6 0.4 2 ij l x a l x a l x a x = − − = − − = = − − = − − = = − − = − − = − = + + = + + = + − 11 12 13 依(2-1-10)式有: 这样 就可以分解成三个数之和: x x x