《机械工程控制基础》课程授课教案（讲义）第二章 系统的数学模型

2.含共轭复数极点情况： b.Sm+.+S+b X(S)-(S+o+jB)(S+a-jB)(S+B)-(S+E.) CS+C C. ++5+a-j9+3+月++s+R (CS+C:)=[X(S)(S+a+jB)(S+o-jB) 令上式两边实、虚部相等，可求得C、C,。 CS+C可通过配方，化成正（余）弦象函数形式→r S+CS+d +1 例6试求：X5)5的拉氏反变换 年-可气品号 S+1 S+1 C=1 8+S+1的两个根为：)9 将XS)式两边同表s+51,并令-分语 1÷sG+ 得C=-l,C=0

2.含共轭复数极点情况：            1 0 3 1 2 3 3 . . . m m n n n b S b S b X S S j S j S P S P C S C C C S j S j S P S P                               1 2      s j s j C S C X S S j S j                       令上式两边实、虚部相等，可求得 C1、C2。 1 2 2 C S C S CS d    可通过配方，化成正（余）弦象函数形式→ 1 L  例 6.试求：   3 2 S 1 X S S S S     的拉氏反变换 解：     1 2 3 3 2 2 2 1 1 1 1 S S C S C C X S S S S S S S S S S              3 C 1 2 S S  1 的两个根为： 1 3 2 2   j 将 X(S)式两边同乘 2 S S  1 ，并令 1 3 2 2   j 则   1 3 1 2 1 3 2 2 2 2 1 S j S j S C S C S              得 1 2 C C    1, 0

x -s+ S+ 51 阁阁 25 2 3.含多重极点的情况 bnS"+.+bS+b, X(S)-S+PyS+P)-S+P】 C C1, C G+t+月t+5++++月sg++2 C C 根据 17 +-e C C,=[xS)(s+R门 C-{Ss+By]}】 GG[9s+A门 倒7.试求：X⑤)=$+2+3的拉氏反变换 (S+1)3

  2 2 2 2 2 2 2 1 1 1 1 2 2 1 1 3 2 2 1 3 1 2 3 1 2 1 3 1 3 2 2 2 2 S S X S S S S S S S S S S                                                                  所以：   2 2 2 3 3 3 3 3 3 cos sin 1 sin cos 1 2 3 2 3 2 2 t t t x t e t e t e t t                   3.含多重极点的情况                 1 0 1 1 1 11 1 1, 1 1, 1 1 1 1 1 . . . . . m m r r n r r r r j n r r r j r r n b S b S b X S S P S P S P C C C C C C S P S P S P S P S P S P                              根据     1 1 1 1 1 1 1 ! k p t k t L L e S P k                                  1 1 1 1 1 1 1, 1 1 2 1, 1 2 1 11 1 1 : 1 ( )! 1 1 ! r j r r s p r r s p r r j s p r r r s p C C x S S P d C x S S P ds d C x S S P r j ds d C x S S P r ds                                                              例 7. 试求：     2 3 2 3 1 S S X S S     的拉氏反变换

:高高品 C=[x(S)-(S+门=S2+2S+3=2 c-{[x(6+]},-s+2以=0 c=[xssy门}-21 xX5)5可*5市 2 故：x(=2e+e 五.用拉氏变换求常系数线性徽分方程 例8.解方程：()+5()+6y()=6,其中，[(0)=2，y(0)=2] 解：根据微分定理有sS-50-0+5[SS-o]+6S)-号 (S+55+6r65)-9+25+2 将器将 -号品g2 所以：y(0=1+5e”-4e 由上例可见，用L解微分方程的步骤： （1)对微分方程进行L (2)做因变量的→求出微分方程的时间解

解：         2 13 12 11 3 3 2 2 3 1 1 1 1 S S C C C X S S S S S               3 2 13 1 1 1 2 3 2 S S C X S S S S                      3 12 1 1 1 2 2 0 S S d C X S S S ds                         2 3 11 2 1 1 1 1 2 1 2! 2 S d C X S S ds                       3 2 1 1 1 X S S S      故:   2 t t x t t e e     五.用拉氏变换求常系数线性微分方程 例 8.解方程： y t y t y t      5 6 6     ,其中，   y y 0 2, 0 2        解：根据微分定理有             2 6 S Y S Sy y SY S y Y S 0 0 5 0 6 S               2 6 S S Y S S 5 6 2 12 S             2 2 2 1 2 3 2 12 6 2 12 6 5 6 2 3 1 5 4 2 3 2 3 S S S S Y S S S S S S S C C C S S S S S S                      所以：   2 3 1 5 4 t t y t e e      由上例可见，用 L 解微分方程的步骤： （1）对微分方程进行 L （2）做因变量的 1 L  →求出微分方程的时间解

微分方程上代数方程求解，YS☐上+y0☐→ 解 图2.7解微分方程流程图 上例中，假设初始条件为0，则 5+5沙+6y=6 根据微分定理有(S+55+6jr-号 6 得)sS+s+)s*2*3南 132 所以：y()=e-3e”+2e 例9.系统如图2.8所示，最初是静止的，假定有一单位脉动使系统开 始运动，求系统的运动规律。 +x(0 →60 图2.8k-m系统 解：m()+c()=() 拉氏变换得：(ms2+)X(S)=1 X(S)-m+k子+k 1 =m

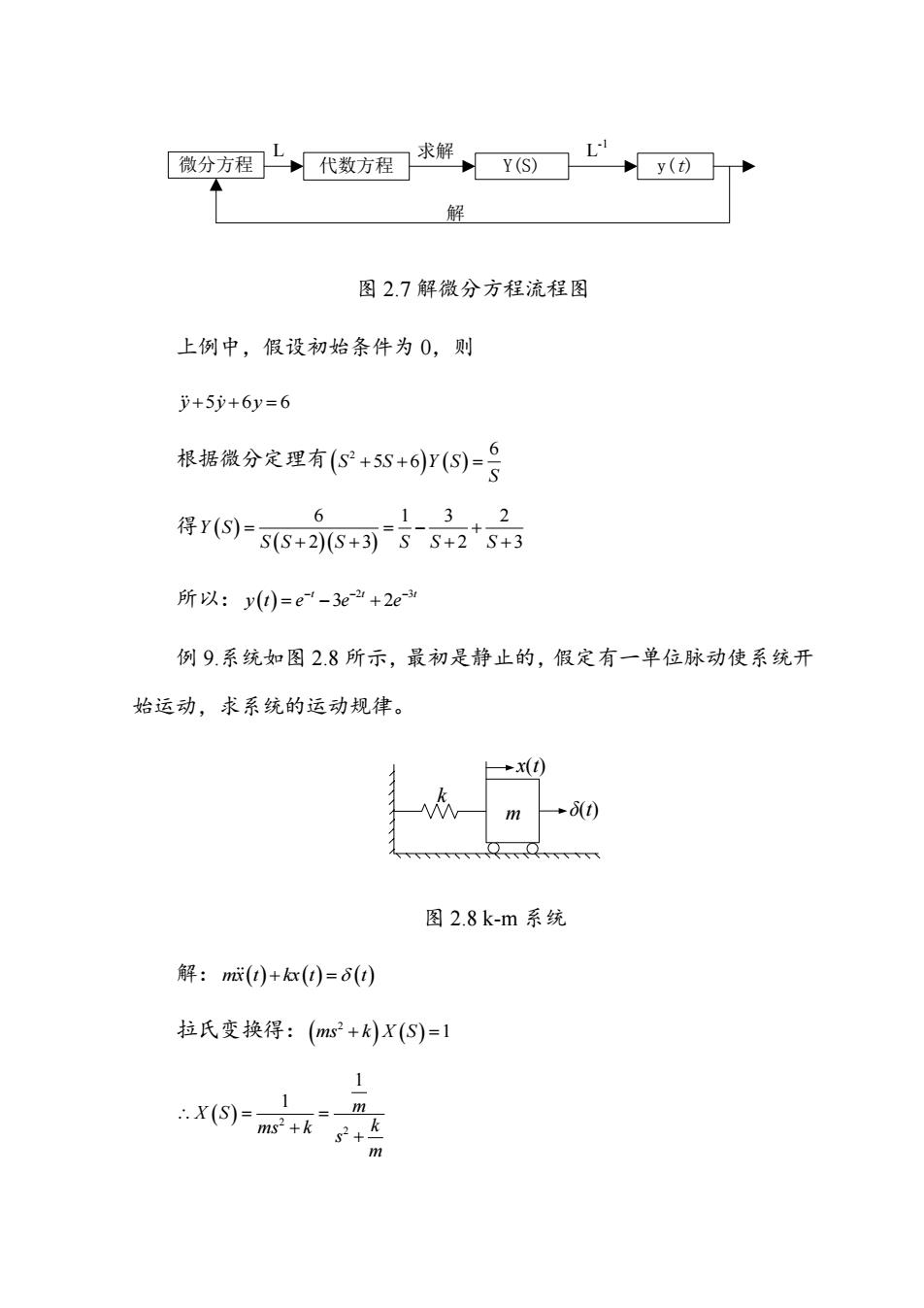
微分方程 代数方程 Y(S) y(t) 求解 L-1 L 解 图 2.7 解微分方程流程图 上例中，假设初始条件为 0，则 y y y    5 6 6 根据微分定理有     2 6 S S Y S 5 6 S    得      6 1 3 2 2 3 2 3 Y S S S S S S S         所以：   2 3 3 2 t t t y t e e e       例 9.系统如图 2.8 所示，最初是静止的，假定有一单位脉动使系统开 始运动，求系统的运动规律。 k m x(t) δ(t) 图 2.8 k-m 系统 解： mx t kx t t          拉氏变换得：     2 ms k X S  1   2 2 1 1 m X S ms k k s m     