《机械工程控制基础》课程授课教案（讲义）第二章 系统的数学模型

-5k"=-e+5eh=-[e= 所以：=1 4.指数函数f0=em(a为正实数) F(S)=L[f()]=L[e-"]-Se"e"d asa 5.正弦函数f=sinot(o为正实数) F(S)-L[f()]-fsinot.ed-Ied[cos] =eowa-wa假e-。 -。己e4ma小esna+mm 引maea :0w ÷F(S)=s2+8 6.余弦函数f)=cosm 同理：FS)=L[cos网]-s+ 7抛物线函数（加速度函数）f0=,120 = 附：拉氏变换表 序号 ( F(s) 1 6) 1

2 2 0 0 0 0 1 1 1 1 1 st st st st tde t e e dt e S S S S S                           所以： L t[ ] 1  4.指数函数   t f t e  （  为正实数）       0 0 1 1 t t st s t F S L f t L e e e dt e S S                                   5.正弦函数 f t t    sin （  为正实数）             0 0 0 0 0 2 2 0 0 0 2 2 1 sin cos 1 1 cos cos cos 1 1 sin sin sin 1 sin st st st st st st st st st F S L f t t e dt e d t S e t t de t e dt S S e d t e t t de S t e dt                                                                             即： 2 2 1 ( ) ( ) S F s F s     ，   2 2 F S S      6.余弦函数 f t t    cos . 同理：     2 2 cos S F S L t S      7.抛物线函数（加速度函数）   1 2 , 0 2 f t t t     2 3 1 1 2 F S L t S         附：拉氏变换表 序号 f t  F s  1  t 1

10 K 4 -40dB/dec 6 e 1 s+& 7 Ie n! (6+a) 8 影 1 5+ 9 sinot 品 10 cos@t 2+0 (s+af+o 12 s+a (G+}+a2 13 -e) 三常用的拉氏变换性质：（不作证明) 1.叠加性 若[]=E,[5]=E() 则[a)+bg.=aF(s+b5) 例3.函数f(0=1-2cosm,求其拉氏变换。 4/01=4-24aag 2.微分定理：

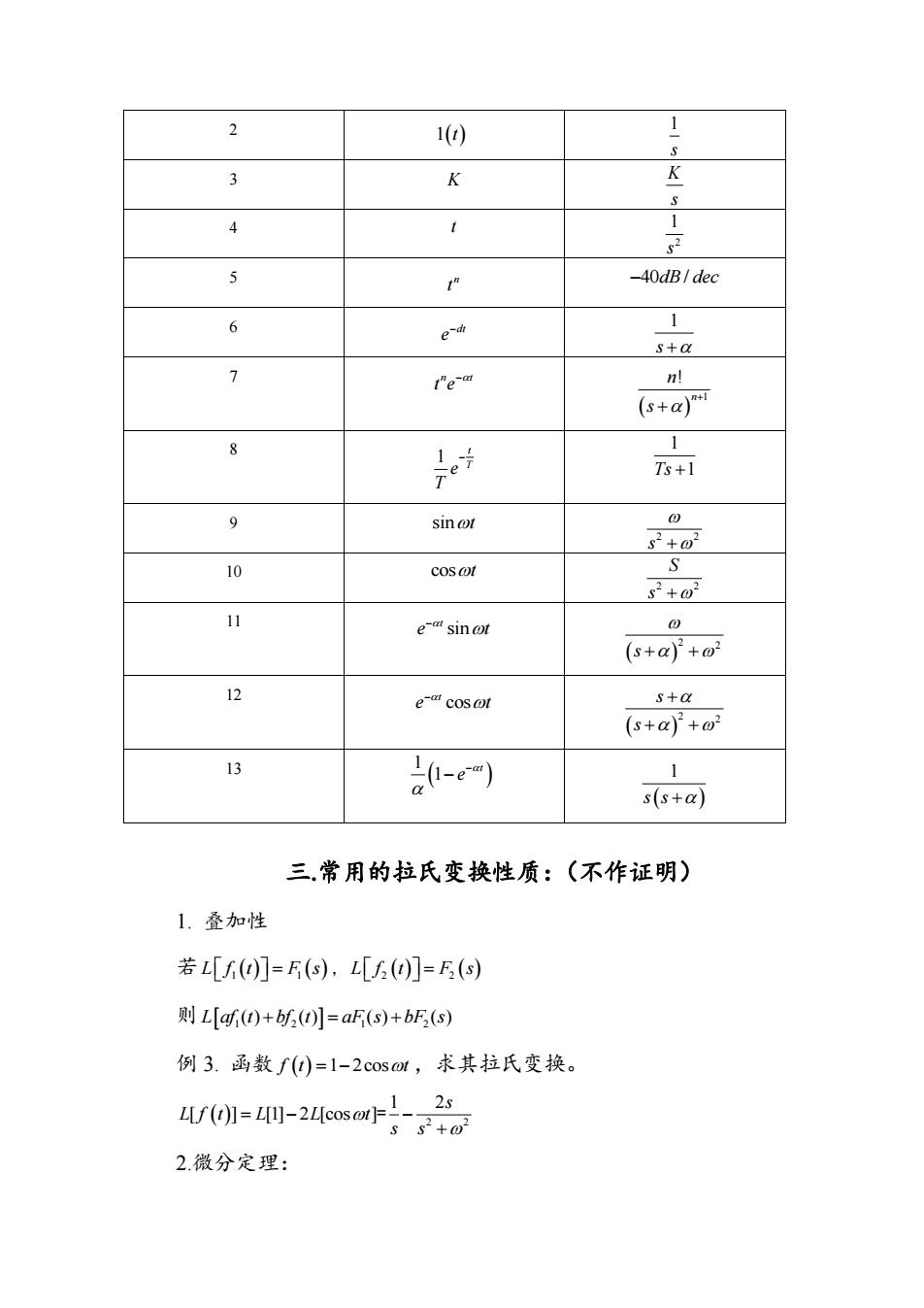
2 1t 1 s 3 K K s 4 t 2 1 s 5 n t 40 / dB dec 6 dt e  1 s  7 n t t e   1 ! n n s    8 1 t T e T  1 Ts 1 9 sint 2 2 s   10 cost 2 2 S s  11 sin t e t      2 2 s      12 cos t e t      2 2 s s       13   1 1 t e       1 s s  三.常用的拉氏变换性质：（不作证明） 1. 叠加性 若 L f t F s   1 1        ， L f t F s   2 2        则 L af t bf t aF s bF s  1 2 1 2 ( ) ( ) ( ) ( )     例 3. 函数 f t t    1 2cos ，求其拉氏变换。   2 2 1 2 [ ] [1] 2 [cos ] s L f t L L t s s       = 2.微分定理：

s-ro -ss0-mro-o 若f(O),f(0)f-(0),这些初始值为0，则：L[(0]=S"F(S) 如任0+20+30+0=20+x0 d d 根据微分定理：(S+2S2+3S+1)x,(S)=(2S+1)x(S) 3积分定理： ro 0]-go+甘ro 若∫f(0)d山，f2(0)dmf(o)d,这些初始值为0，则： (s) 4.位移定理：

                1 2 ' ( 1) 0 0 0 . 0 n n n n n n df t L SF S f dt d f t L S F S S f S f f dt                       若       ' 1 0 , 0 . 0 n f f f  ，这些初始值为 0，则：   ( ) ( ) n n L f t S F S      如 3 2 0 0 0 3 2 0 ( ) ( ) ( ) ( ) 2 3 ( ) 2 ( ) i i d x t d x t dx t dx t x t x t dt dt dt dt      根据微分定理：         3 2 0 2 3 1 2 1 i S S S x S S x S      3.积分定理：                ( ) 1 0 1 1 0 . 0 n n n n F S L f t dt f dt S S F S L f t dt f dt f dt S S S                        若       (2) ( ) 0 , 0 . 0 n f dt f dt f f dt  ，这些初始值为 0，则：     ( ) n 1 n L f t dt F S S       4.位移定理： f(t) t f(t-τ) t

图2.6函数位移示意图 如图2.6所示，原函数)沿时间轴平移x,为f(-)。 L[f(t-r)]=e-"F(S) L e-af(t)=F(S+a) 如[co]s+a旷+o S+a 5.初值定理：时间函数)的初值为imf0=mSF(S) 只有0)存在时才能应用，用来确定系统的初值，而勿需知道原函数。 如：F)=4a求0) (0)=limf()=limsF(S)=limsima 或L+f)=em,f(0)=e°=1 6.终值定理：时间函数)的稳定值（终值)为mf0=mF(S) :F-写a求回 =0 f回)=mr(S)-gs+a 或r+f)=em,f(o)=e*=0 四拉氏反变换 拉氏反变换定义： 0-r[(s]+0e 简单方法：原函数→典型象函数叠加（查表）→)

图 2.6 函数位移示意图 如图 2.6 所示，原函数 f(t)沿时间轴平移  ，为 f t  。         s at L f t e F S L e f t F S a                 如   2 2 cos at S a L e t S a            5.初值定理：时间函数 f(t)的初值为     0 lim lim t S f t SF S    只有 f(0)存在时才能应用，用来确定系统的初值，而勿需知道原函数。 如：   1 F S S a   ，求 f(0)       0 1 0 lim lim lim lim 1 1 t S S S S f f t SF S S a a S            或 1 L  →   at f t e  ，   0 f e 0 1   6.终值定理：时间函数 f(t)的稳定值（终值）为     0 lim lim t S f t SF S    如：   1 F S , S a   求 f      0 0 lim lim 0 S S S f SF S   S a      或 1 L  →   at f t e  ， f e   0     四.拉氏反变换 拉氏反变换定义：     1 x t L x S       →     1 2 j st j x t x S e ds j          简单方法：原函数→典型象函数叠加（查表）→f(t)

例4试求：X=5的拉氏反变换 25-1 解：r[xS]=r。S] (+1)2+22 [s+11 2 s++2*s++2 cos21-esin2 常遇到如下形式的有理分式： X(S=65+6S++65+6 S”+an1++aS+a 使分母为0的S值→极点，使分子为0的S值+零，点 可通过部分分式展开法求 1.只含不同单极，点的情况 bnS"++bS+b。 X)=s8+6+As4*s月++s5 C C. C C。一为S=-P极点处的留数。 C.=[xS)(S+P】- 将X(S)进行，得：x(0=L[X(S)]=Cem+C,ew++Cew S+3 例5.试末X)-2的拉氏反变换 S+3 S+3 G-[68gel2,6 21 X5)3年5中2→0=2e-e

例 4. 试求：   2 2 5 S X S S S    的拉氏反变换 解：       1 1 1 2 2 2 1 1 2 5 1 2 S S L x S L L S S S                                  1 1 2 2 2 2 1 1 2 1 2 1 2 2 1 cos 2 sin 2 2 t t S L L S S e t e t                               常遇到如下形式的有理分式：   1 1 1 0 1 1 1 0 . . m m m m n n n b S b S b S b X S S a S a S a              使分母为 0 的 S 值→极点，使分子为 0 的 S 值→零点 可通过部分分式展开法求 1 L  1.只含不同单极点的情况        1 0 1 2 1 2 1 2 . . . m m n n n b S b S b C C C X S S P S P S P S P S P S P               Cn—为 n S P   极点处的留数。     k k k s P C X S S P         将 X(S)进行 1 L  ，得：     1 1 2 1 2 . n p t p t p t n x t L X S C e C e C e              例 5.试求   2 3 3 2 S X S S S     的拉氏反变换. 解：      1 2 2 3 3 3 2 1 2 1 2 S S C C X S S S S S S S                1   1 3 1 2 1 2 s S C S S S                ， 2 C  1     2 1 2 2 1 2 t t X S x t e e S S          