
例1.证明三角形余弦定理 c2 a2+b2-2abcos0 证:如图.设 CB-a,CA=b,AB= 则 c-a-b c=(区-)=aa+b.b-2a-6 =lap+B2-2acos0 a=a,b=b,c=7 c2 a2 +b2 -2abcos0 HIGH EDUCATION PRESS 机动目录上页下页返回结束
A B C a b c 例1. 证明三角形余弦定理 2 cos 2 2 2 c = a + b − ab 证: 则 2 cos 2 2 2 c = a + b − ab 如图 . 设 CB = a , CA = b, AB = c = 2 c ( a − b)( a − b)= a a + b b − 2a b 2 = a 2 + b − 2 a b cos a = a , b = b , c = c 机动 目录 上页 下页 返回 结束

4.数量积的坐标表示 设a=ai+a,j+a.k,b=bi+b,j+bk,则 ab=(a,i+a,了+a.)(b.i+b,j+b飞) i.i=j.f=k.k=1,T.j=j.k-ki-0 a-b=axbx +ayby +a-b 两向量的夹角公式 当a,b为非零向量时,由于a.乃=acos0,得 a.b axbx +ayby a-b- cos a va+a5+a√b+b+b HIGH EDUCATION PRESS ◆00⊙8 机动目录上页下页返回结束
4. 数量积的坐标表示 设 则 = 0 x x y y z z =a b + a b + a b 当 为非零向量时, cos = = x x y y z z a b + a b + a b 2 2 2 x y z a + a + a 2 2 2 x y z b + b + b 由于 a b cos a a i a j a k , = x + y + z b b i b j b k , = x + y + z ( a i + a j + a k ) x y z (b i b j b k ) x + y + z i j = j k = k i a b a b 两向量的夹角公式 , 得 机动 目录 上页 下页 返回 结束
填空题1分 ⊙设置 设a=(1,1,-4),b=(2,0,-2) 则(a+(a-b= [填空1] 正常使用填空题需3.0以上版本雨课堂 HIGH EDUCATION PRESS 作答
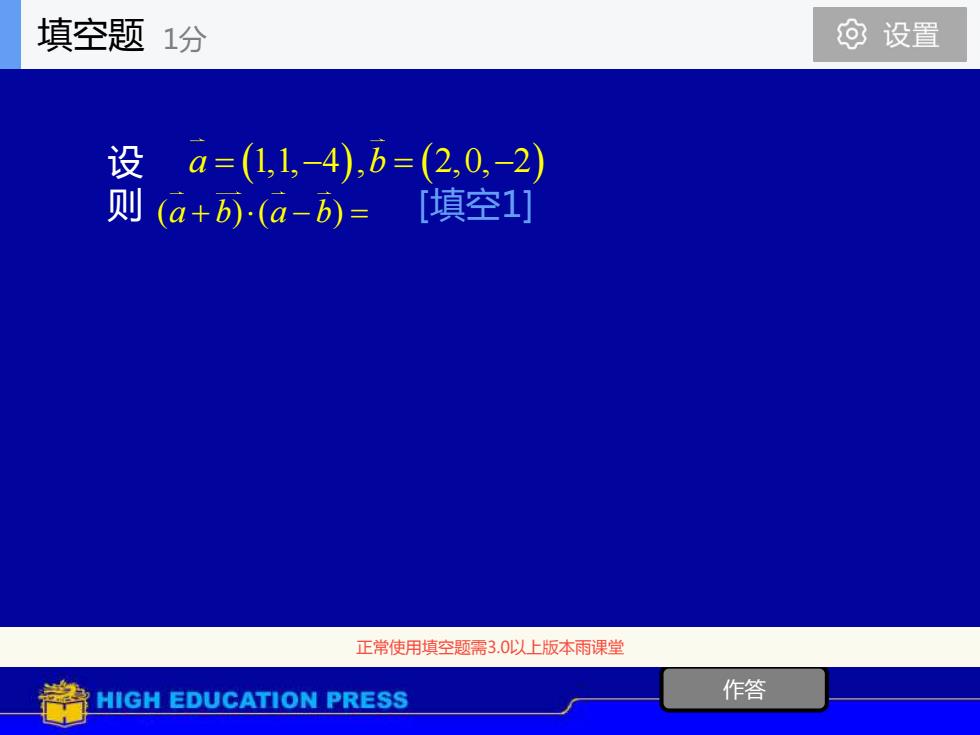
设 则 [填空1] 作答 正常使用填空题需3.0以上版本雨课堂 a b = − = − (1,1, 4 , 2,0, 2 ) ( ) ( ) ( ) a b a b + − = 填空题 1分