
(5)[0,1山≈(0,1) 构造区间[0,1]与(0,1)之间1-1映射的 一个例子。我们知道全体有理数的集合是 可数的,于是(0,1)区间中的有理数是可数 的,不妨将它们排成a1,a2,an,的 形式。 而闭区间[0,1]比区间(0,1)多两个数0 和1,它们是有理数,于是可建立闭区间[0, 1]中的有理数到区间(0,1)中的有理数的1-1 映射o1:
(5) [0,1] (0,1) 构造区间[0,1]与(0,1)之间1-1映射的 一个例子。我们知道全体有理数的集合是 可数的,于是(0,1)区间中的有理数是可数 的,不妨将它们排成a1 , a2 , ., an , .的 形式。 而闭区间[0,1]比区间(0,1)多两个数0 和1,它们是有理数,于是可建立闭区间[0, 1]中的有理数到区间(0,1)中的有理数的1-1 映射1:

0,1,a1, a1,a2a3 a4’ .,ant2 令区间[0,1]中的无理数到区间(0,1)中的无理数 的1-1映射o,为自己对应自己。则映射0=01U02 为区间[0,1]到区间(0,1)的1-1映射。从而区间 [0,1]与(0,1)等势
令区间[0,1]中的无理数到区间(0,1)中的无理数 的1-1映射2为自己对应自己。则映射= 1∪2 为区间[0, 1]到区间(0,1)的1-1映射。从而区间 [0,1]与(0,1)等势。 0, 1, a1, a2,.,an,. . . a1,a2,a3, a4,., an+2,

定理9.1 (1)A≈A (2)若A≈B,则B≈A 3)若A≈B,B≈C,则A≈C
定理9.1 (1) A A (2) 若A B,则B A (3) 若A B, B C,则A C
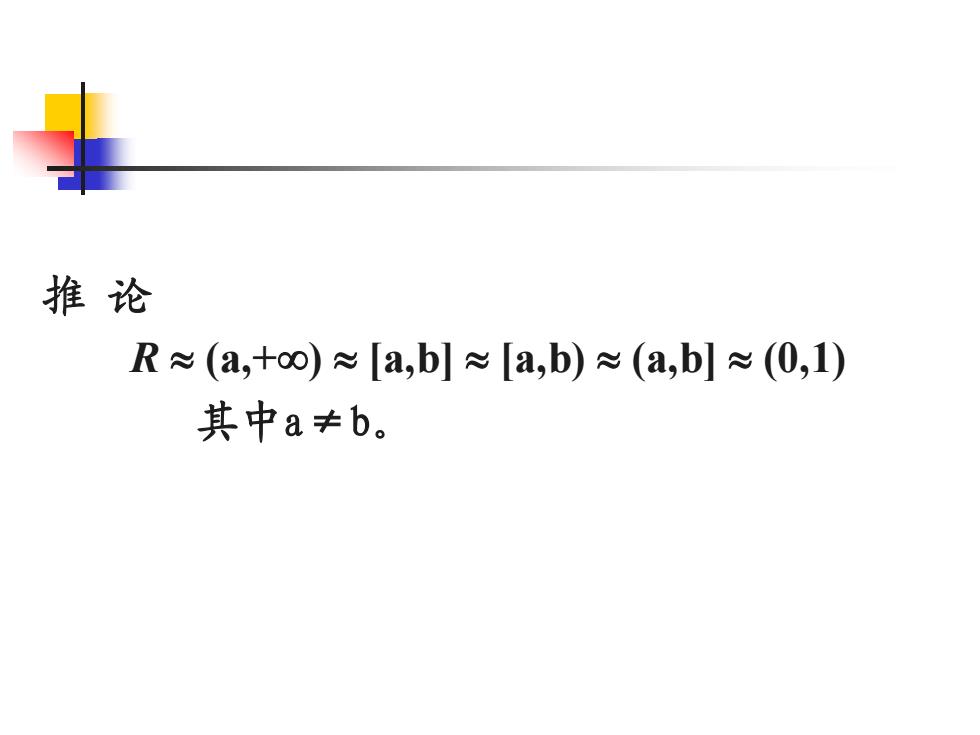
推论 R≈(a,+o∞)≈a,b]≈[a,b)≈(a,bl≈(0,1) 其中a≠b
推 论 R (a,+) [a,b] [a,b) (a,b] (0,1) 其中a≠b

定理9.2(康托尔定理) (1)N¥R (2)对任意集合A都有A*P(A)
定理9.2(康托尔定理) (1) N R (2) 对任意集合A都有 A P(A)