
§1热传导方程及其定解问题的导出 热传导方程的导出 定解问题的提法 扩散方程 逾国
§1 热传导方程及其定解问题的导出 1 热传导方程的导出 2 定解问题的提法 3 扩散方程

热传导方程的导出 u(x,y,Z,t)表示表示物体在位置(x,y,z)处及时刻t的温度 (1)预备知识 (i)高斯公式:设2是3中的有界开域,2的边界T分片光滑,记 五=2U.设函数p(x,y,z,Q(x,y,z),R(x,y,z)在五上连续,在2内有 一阶偏导数,则 y dsc)Ros()ds
1 热传导方程的导出 𝑢(𝑥,𝑦, 𝑧,𝑡)表示表示物体在位置(𝑥, 𝑦, 𝑧)处及时刻𝑡的温度 (1)预备知识 (ⅰ)高斯公式:设Ω是R 3中的有界开域,Ω的边界Γ分片光滑,记 Ωഥ = Ω ∪ Γ.设函数𝑝(𝑥, 𝑦, 𝑧),𝑄(𝑥, 𝑦, 𝑧),𝑅(𝑥, 𝑦, 𝑧)在Ωഥ上连续,在Ω内有 一阶偏导数,则 ම𝛺 𝜕𝑝 𝜕𝑥 + 𝜕𝑄 𝜕𝑦 + 𝜕𝑅 𝜕𝑧 𝑑𝑥𝑑𝑦 ⅆ𝑧 =ඵ 𝛤 ሾ𝑝cos 𝑛, 𝑥 + 𝑄cos 𝑛, 𝑦 + 𝑅cos(𝑛, 𝑧)]𝑑𝑆

1热传导方程的导出 其中(cos(n,x),cos(n,y),cos(n,z))是Γ上的面积微元 dS的外法线方向的方向余弦. (ii)Fourieri热试验定律: 物体在无穷小时段dt内沿法线方向n流过一个无穷小面积dS的热量dQ与物体温 度沿曲面dS法线方向的方向导数成正比,即 dn dQ=-k(x,y,z)dSdt(k是物体在(x,y,z)点的热传导系数
1 热传导方程的导出 其中(cos(𝑛, 𝑥),cos(𝑛, 𝑦),cos(𝑛, 𝑧))是Γ上的面积微元 𝑑𝑆的外法线方向的方向余弦. (ⅱ)Fourier热试验定律: 物体在无穷小时段𝑑𝑡内沿法线方向𝑛流过一个无穷小面积𝑑𝑆的热量𝑑𝑄与物体温 度沿曲面𝑑𝑆法线方向的方向导数𝜕𝑢 𝜕𝑛成正比,即 𝑑𝑄 = −𝑘(𝑥, 𝑦, 𝑧) 𝜕𝑢 𝜕𝑛 𝑑𝑆 𝑑𝑡(𝑘是物体在(𝑥, 𝑦, 𝑧)点的热传导系数)
1热传导方程的导出 G d 国色
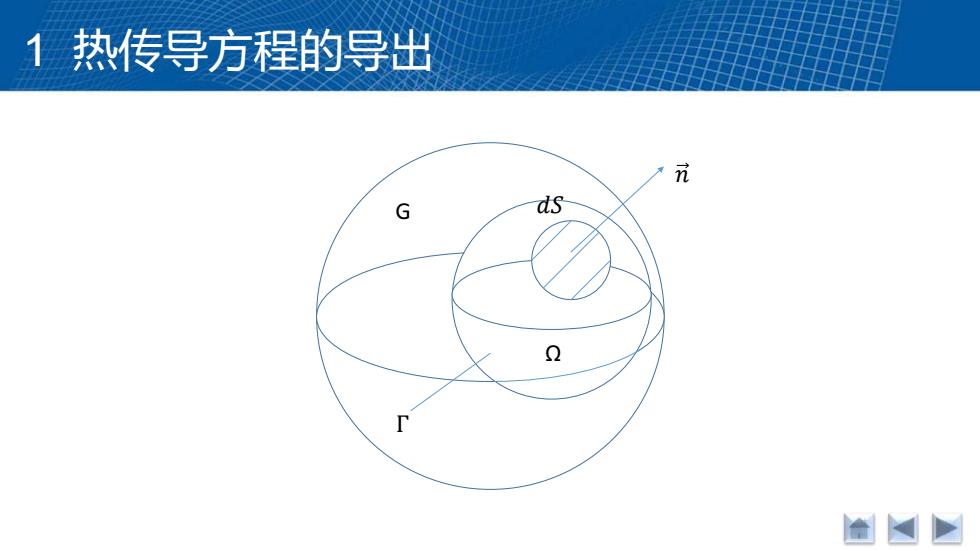
𝑛 G Ω Γ 𝑑𝑆 1 热传导方程的导出

1热传导方程的导出 (2)方程的导出 问题:空间某物体G,建立温度函数u(x,y,z,t)所满足的微分方程. 基本关系式:在物体G内任取一闭曲线「,它包含的区域记为Q,在 上,从时刻t到时刻t2热量流动成立热平衡方程式 流入的热量Q1=引起温度变化所吸收的热量Q2 由Fourier热试验定律,从t1到t2流入的热量为 Q,={们kgy器arr是n的边第)
1 热传导方程的导出 问题:空间某物体G,建立温度函数𝑢(𝑥,𝑦, 𝑧,𝑡)所满足的微分方程. 基本关系式:在物体G内任取一闭曲线Γ,它包含的区域记为Ω,在 Ω上,从时刻𝑡1到时刻𝑡2热量流动成立热平衡方程式 流入的热量𝑄1=引起温度变化所吸收的热量𝑄2 由Fourier热试验定律,从𝑡1到𝑡2流入Ω的热量为 𝑄1 = න 𝑡1 𝑡2 ඵ 𝛤 𝑘(𝑥, 𝑦, 𝑧) 𝜕𝑢 𝜕𝑛 ⅆ𝑠 ⅆ𝑡(Γ是Ω的边界) (2)方程的导出