
本次课主要内容 (一)、树的概念与应用 (二)、树的性质 (三)、树的中心与形心
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 本次课主要内容 (一)、树的概念与应用 (二)、树的性质 (三)、树的中心与形心
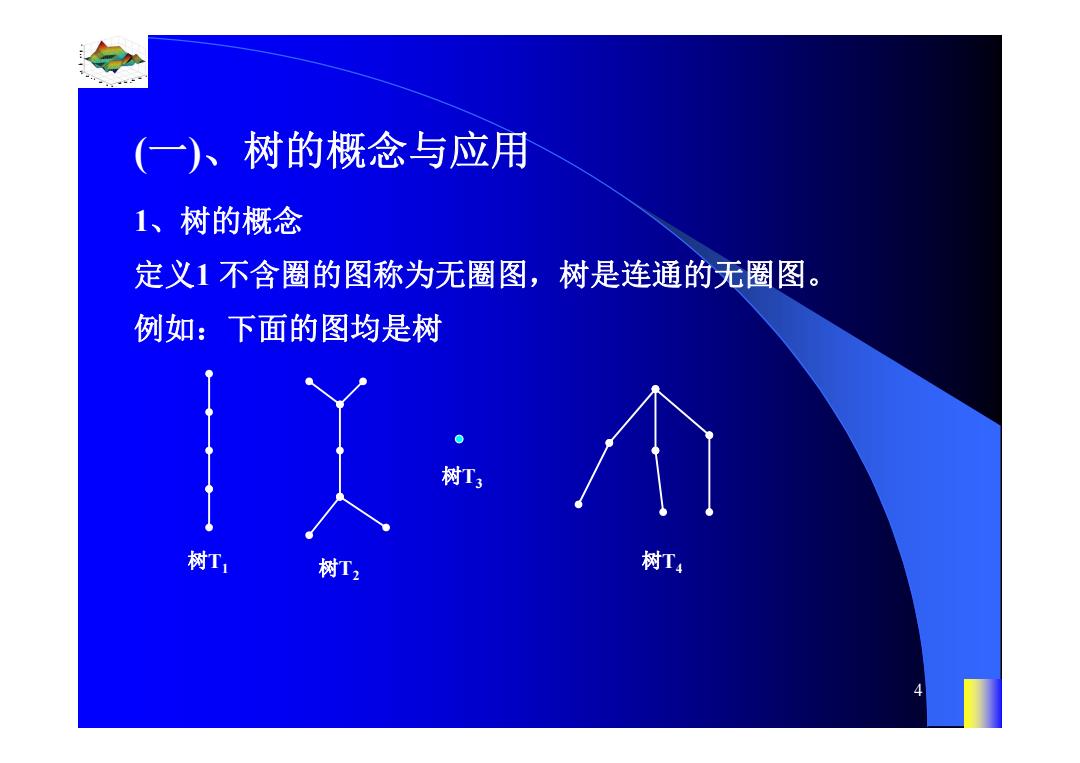
(一)、树的概念与应用 1、树的概念 定义1不含圈的图称为无圈图,树是连通的无圈图。 例如:下面的图均是树 树T3 树T, 树T2 树T4
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 1、树的概念 (一)、树的概念与应用 定义1 不含圈的图称为无圈图,树是连通的无圈图。 例如:下面的图均是树 树T1 树T2 树T3 树T4

定义2称无圈图G为森林。 注:(1)树与森林都是单图; (2)树与森林都是偶图。 例1画出所有不同构的6阶树。 解:按树中存在的最长路进行枚举。6阶树中能够存在 的最长路最小值为2,最大值为5。 火义平
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 定义2 称无圈图G为森林。 注: (1)树与森林都是单图; (2) 树与森林都是偶图。 例1 画出所有不同构的6阶树。 解:按树中存在的最长路进行枚举。6阶树中能够存在 的最长路最小值为2,最大值为5

2、树的应用 树是图论中应用最为广泛的一类图。在理论上,由 于树的简单结构,常常是图论理论研究的“试验田” 在实际问题中,许多实际问题的图论模型就是树。 例2族谱图与树 要把一个家族的繁衍情况简洁直观表达出来,用点 表示家族中成员,成员x是成员y的儿女,把点x画在点 y的下方,并连线。如此得到的图,是一颗树,称为根 树。示意如下: 根树
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 树是图论中应用最为广泛的一类图。在理论上,由 于树的简单结构,常常是图论理论研究的“试验田”。 在实际问题中,许多实际问题的图论模型就是树。 例2 族谱图与树 2、树的应用 要把一个家族的繁衍情况简洁直观表达出来,用点 表示家族中成员,成员x是成员y的儿女,把点x画在点 y的下方,并连线。如此得到的图,是一颗树,称为根 树。示意如下: 根树

实际上,根树是许多问题的模型,如社会结构,计算机 数据结构,数学中的公式结构,分类枚举表示等。 例3道路的铺设与树 假设要在某地建造4个工厂,拟修筑道路连接这4处。 经勘探,其道路可按下图的无向边铺设。现在每条边的 长度已经测出并标记在图的对应边上,如果我们要求铺 设的道路总长度最短,这样既能节省费用,又能缩短 工期,如何铺设? 1V2 4
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 实际上,根树是许多问题的模型,如社会结构,计算机 数据结构,数学中的公式结构,分类枚举表示等。 例3 道路的铺设与树 假设要在某地建造4个工厂,拟修筑道路连接这4处。 经勘探,其道路可按下图的无向边铺设。现在每条边的 长度已经测出并标记在图的对应边上,如果我们要求铺 设的道路总长度最短,这样既能节省费用 ,又能缩短 工期 ,如何铺设? v2 v3 v4 e2 e3 e4 v1 e1 e5 e6