
课程网站 http://math.sjtu.edu.cn/course/skymath/ 第二讲智者的沉思:从勾股定理到费马猜想 算术基本定理可以看成是一个关于正整数的乘法性质的结论.自然数还 有一个基本运算,即加法。 课题问答:什么是加法?更进一步,什么是减法?什么是乘法、除 法?… 关于自然数加法性质的结论往往与乘法混合在一起,其中最著名最古 老的是 勾股定理直角三角形的两直角边的平方和等于斜边的平方.如果 以a,b,c记直角三角形的两个直角边与斜边的长,则有a2+2=c2. 注1.勾股定理还称为商高定理(内容是“勾三股四弦五”这一特 例),我国最早记载于《周髀算经》(约前一世纪):陈子(约前7世纪) 测日法“若求邪至日者,以日下为勾,日高为股,勾股各自乘,并开方而 除之,得邪至日者”.西方称勾股定理为毕达哥拉斯(Pythagoras)定理, 百牛定理,或驴桥定理(Asses'Bridge,等腰三角形两底角相等),约前570- 前495.现有记载中最早发现相同结果的是古巴比伦,大约前2000-前1700年 1
➅➜✤Õ http://math.sjtu.edu.cn/course/skymath/ ✶✓ù ➐ö✛➐❣➭❧✄✘➼♥✔↕êß➂ ➂â➘✢➼♥➀➧✇↕➫➌❻✬✉✔✒ê✛➛④✺➓✛✭Ø. ❣✱ê❸ ❦➌❻➘✢✩➂➜❂❭④✧ ➅❑➥❽➭➓♦➫❭④➸➁❄➌Ú➜➓♦➫⑦④➸➓♦➫➛④✦Ø ④➸..... ✬✉❣✱ê❭④✺➓✛✭Ø✥✥❺➛④➲Ü✸➌å➜Ù➙⑩❮➯⑩✔ P✛➫ ✄✘➼♥ ❺✍♥✍✴✛ü❺✍❃✛➨➄Ú✤✉✒❃✛➨➄. ❳❏ ➧a, b, cP❺✍♥✍✴✛ü❻❺✍❃❺✒❃✛⑧➜❑❦a 2 + b 2 = c 2 . ✺1. ✄✘➼♥❸→➃û♣➼♥↔❙◆➫✴✄♥✘♦✉✃✵ù➌❆ ⑦↕➜➲■⑩❅P✶✉✺➧✕➂➨✻(✕❝➌➢❱)➭ ➑❢↔✕❝7➢❱↕ ÿ❋④✴❡➛✑➊❋ö➜➧❋❡➃✄➜❋♣➃✘➜✄✘❼❣➛➜➾♠➄✌ Ø❷➜✚✑➊❋ö✵. Ü➄→✄✘➼♥➃✳❼①✳❞(Pythagoras)➼♥➜ ③Ú➼♥➜➼➻①➼♥(Asses’ Bridge➜✤✛♥✍✴ü✳✍❷✤)➜✕❝570- ❝495. ②❦P✶➙⑩❅✉②❷Ó✭❏✛➫✔♥✬Ô➜➀✕❝2000-❝1700❝. 1
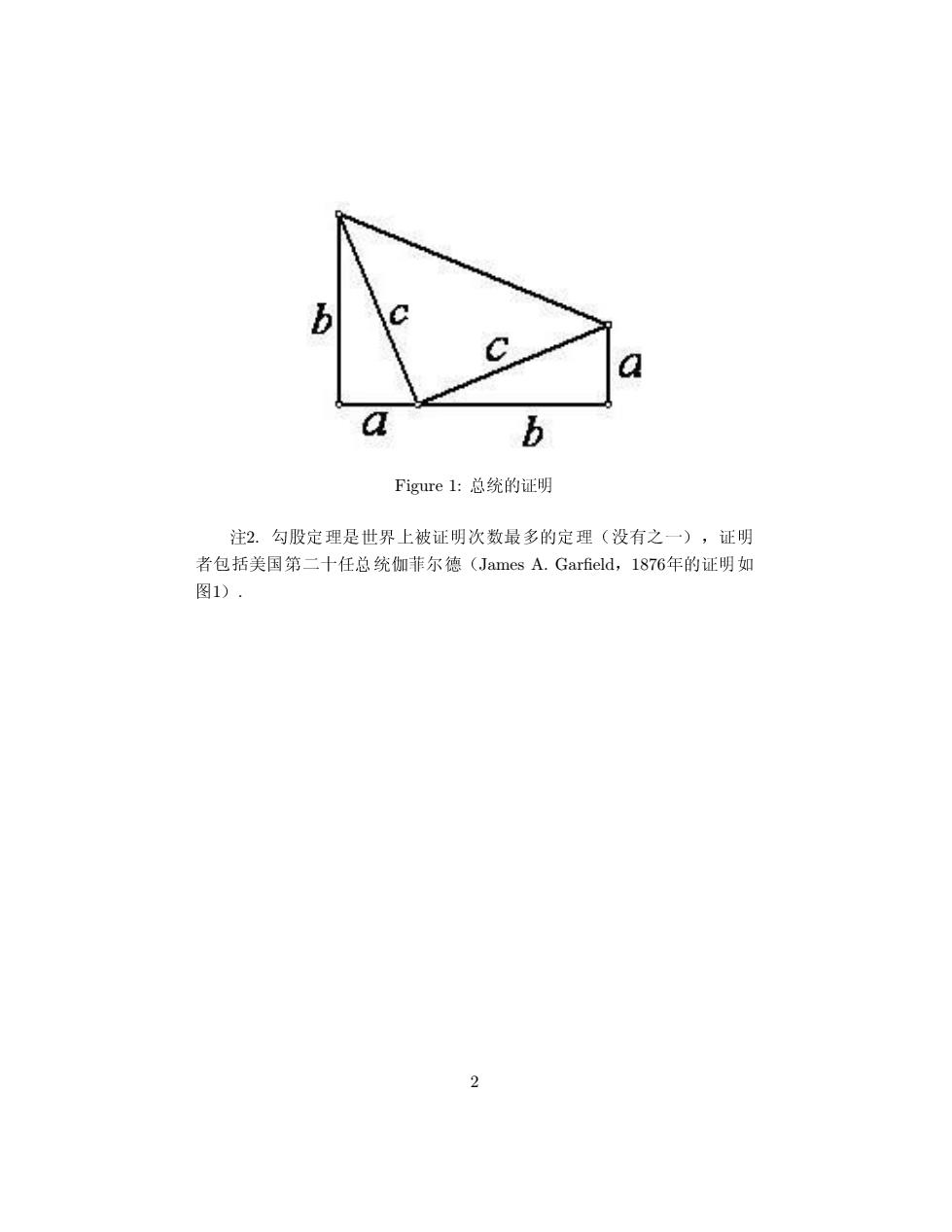
b a a b Figure1:总统的证明 注2.勾股定理是世界上被证明次数最多的定理(没有之一),证明 者包括美国第二十任总统伽菲尔德(James A.Garfield,1876年的证明如 图1). 2
Figure 1: ♦Ú✛②➨ ✺2. ✄✘➼♥➫➢✳þ✚②➨❣ê⑩õ✛➼♥↔✈❦❷➌↕➜②➨ ö➑✮④■✶✓➏❄♦Ú➩➍✏✙↔James A. Garfield➜1876❝✛②➨❳ ã1↕. 2
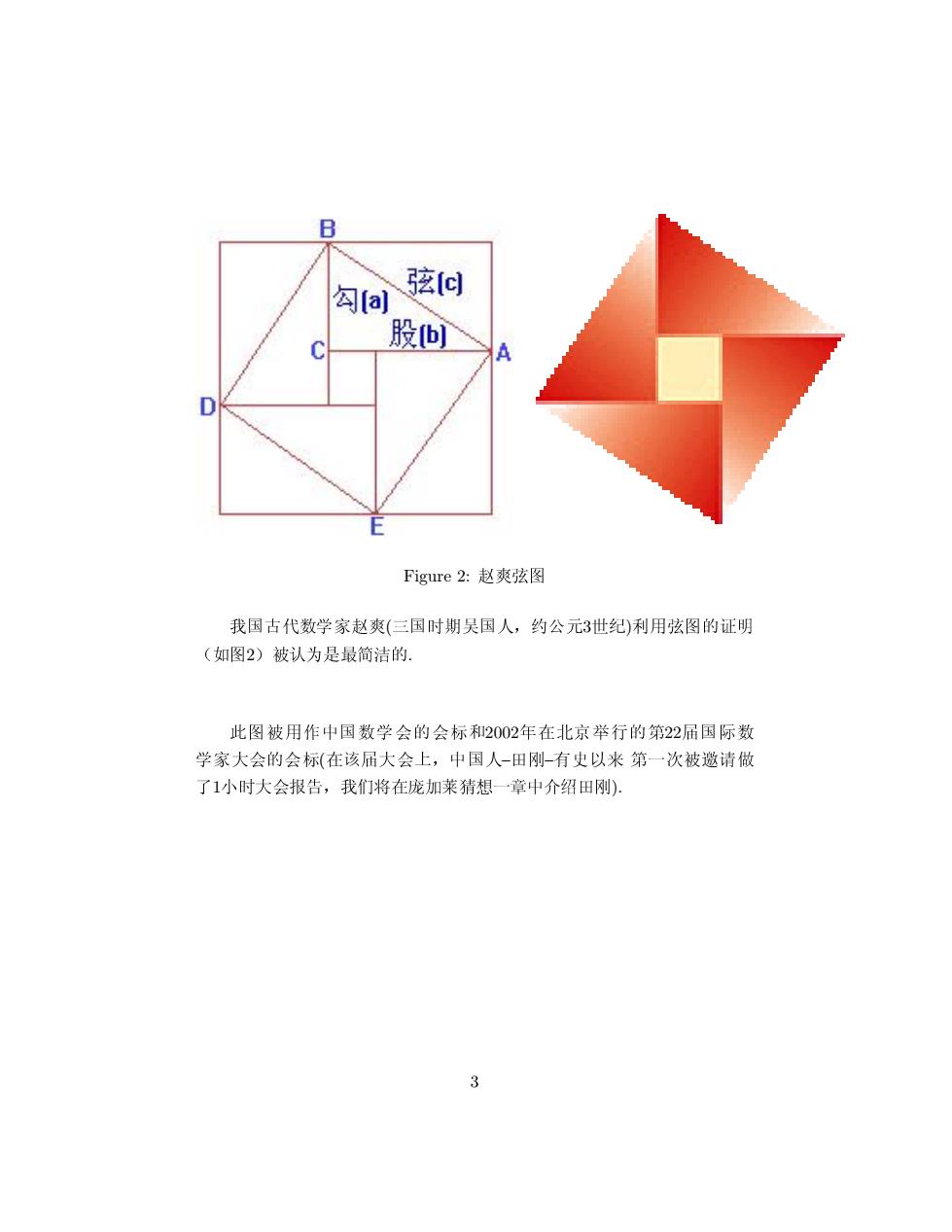
B 勾a 弦d C 股 A D Figure2:赵爽弦图 我国古代数学家赵爽(三国时期吴国人,约公元3世纪)利用弦图的证明 (如图2)被认为是最简洁的. 此图被用作中国数学会的会标利和2002年在北京举行的第22届国际数 学家大会的会标(在该届大会上,中国人-田刚-有史以来第一次被邀请做 了1小时大会报告,我们将在庞加莱猜想一章中介绍田刚) 3
Figure 2: ë❲✉ã ➲■✔➇ê➷❬ë❲(♥■➒Ï➬■❁➜✕ú✄3➢❱)⑤❫✉ã✛②➨ ↔❳ã2↕✚❅➃➫⑩④✬✛. ❞ã✚❫❾➙■ê➷➡✛➡■Ú2002❝✸✏➤Þ✶✛✶22✸■❙ê ➷❬➀➡✛➡■(✸❚✸➀➡þ➜➙■❁–❳❢–❦↕➧✺ ✶➌❣✚✚➒❽ ✡1✂➒➀➡✞✇➜➲❶ò✸✡❭✹ß➂➌Ù➙✵☛❳❢). 3

注2.高维推)广与欧氏距离 由勾股定理可知,平面(R2)上两点x=(x1,x2),y=(1,2)的距离为 d(x,)=V(x1-1)2+(x2-y2)2 所以单位圆(周)的方程是x子+x号=1(通常将平面上点的坐标记 为(x,y),因此单位圆的方程写为x2+y2=1) 空间(R3)中两点x=(c1,x2,x3),y=(y1,2,3)的距离为 d(x,)=V(x1-h)2+(c2-2)2+(x3-g)2 上面的公式可以看成是3维空间中的勾股定理,比如由此公式可知,3 维空间中的单位球(面)的方程是x子+x号+x=1(通常将空间中点的坐标 记为(x,,),因此单位球的方程写为x2+y2+2=1) 般地,勾股定理可以推到n维(实)空间R”,任意两点x=(x1,x2,·,x),y= (1,2,·,n)的距离为 d(x,y)=V(c1-h)2+(x2-2)2+·+(xn-yn)2 所以n维空间R”中的单位球(面)的方程是x子+x子+·+x品=1. 习题2:勾股定理反映了直角三角形三条边长之间的关系,试研究面积 的勾股定理 4
✺2. ♣➅í✷❺î➻å❧ ❞✄✘➼♥➀⑧➜➨→(R 2 )þü✿ x = (x1, x2), y = (y1, y2)✛å❧➃ d(x, y) = p (x1 − y1) 2 + (x2 − y2) 2. ↕➧ü➔☛(➧)✛➄➜➫ x 2 1 + x 2 2 = 1 (Ï⑦ò➨→þ✿✛❿■P ➃(x, y)➜Ï❞ü➔☛✛➄➜✕➃ x 2 + y 2 = 1). ➌♠(R 3 )➙ü✿x = (x1, x2, x3), y = (y1, y2, y3)✛å❧➃ d(x, y) = p (x1 − y1) 2 + (x2 − y2) 2 + (x3 − y3) 2. þ→✛ú➟➀➧✇↕➫3-➅➌♠➙✛✄✘➼♥➜✬❳❞❞ú➟➀⑧➜3- ➅➌♠➙✛ü➔➙(→)✛➄➜➫ x 2 1 + x 2 2 + x 2 3 = 1 (Ï⑦ò➌♠➙✿✛❿■ P➃(x, y, z)➜Ï❞ü➔➙✛➄➜✕➃x 2 + y 2 + z 2 = 1). ➌❸✴➜✄✘➼♥➀➧í✷✔n ➅(➣)➌♠R n➜❄➾ü✿x = (x1, x2, · · · , xn), y = (y1, y2, · · · , yn)✛å❧➃ d(x, y) = p (x1 − y1) 2 + (x2 − y2) 2 + · · · + (xn − yn) 2. ↕➧ n ➅➌♠R n➙✛ü➔➙(→)✛➄➜➫ x 2 1 + x 2 2 + · · · + x 2 n = 1. ❙❑2➭✄✘➼♥❻◆✡❺✍♥✍✴♥❫❃⑧❷♠✛✬❳➜➪ï➘→➮ ✛✄✘➼♥. 4

注3.如果正整数a,b,c满足条件a2+b2=c2,则称(a,b,c)为一个毕达 哥拉斯理元组(Pythagorean triple).比如,(3,4,5),(5,12,13)是毕达哥 拉斯理元组.如果一个毕达哥拉斯理元组中的整数α,b,c两两互素,则称其 为本原的(primitive).比如,(3,4,5),(5,12,13)均是本原毕达哥拉斯理元 组,但(6,8,10)不是本原毕达哥拉斯理元组. 随堂练习1:求你能写出的最大的本原毕达哥拉斯理元组. 当然存在无限多个本原毕达哥拉斯理元组,为什么? 思考题:单位圆周x2+y2=1上有多少个有理点(即两个坐标都为有理 数的点)? 思考题:圆周x2+y=3上有多少个有理点?请比较上面的思考题 5
✺3. ❳❏✔✒êa, b, c÷✈❫❻a 2 + b 2 = c 2 ➜❑→(a, b, c)➃➌❻✳❼ ①✳❞♥✄⑤(Pythagorean triple). ✬❳➜(3, 4, 5)➜(5, 12, 13) ➫✳❼① ✳❞♥✄⑤. ❳❏➌❻✳❼①✳❞♥✄⑤➙✛✒ê a, b, cüü♣❷➜❑→Ù ➃✢✝✛(primitive). ✬❳➜(3, 4, 5)➜(5, 12, 13) þ➫✢✝✳❼①✳❞♥✄ ⑤➜✂(6, 8, 10) Ø➫✢✝ ✳❼①✳❞♥✄⑤. ➅✱ö❙1➭ ➛❭❯✕Ñ✛⑩➀✛✢✝✳❼①✳❞♥✄⑤. ✟✱⑧✸➹⑩õ❻✢✝✳❼①✳❞♥✄⑤➜➃➓♦? ❣⑧❑➭ü➔☛➧x 2 + y 2 = 1 þ❦õ✟❻❦♥✿(❂ü❻❿■Ñ➃❦♥ ê✛✿)➸ ❣⑧❑➭☛➧ x 2 + y 2 = 3þ❦õ✟❻❦♥✿➸➒✬✖þ→✛❣⑧❑. 5