/966 Let f(n)be the unit-sample response from the input u(n) to the state x(n),and let g(n)be the unit-sample response from the error e(n)to the output yn).It is necessary to scale the inputs to multipliers in order to avoid internal overflow. d b u(n) y(n) f(n) x(n) e(n) d u(n) y(n) x(n+1) g(n) e(n) 2021年2月 16
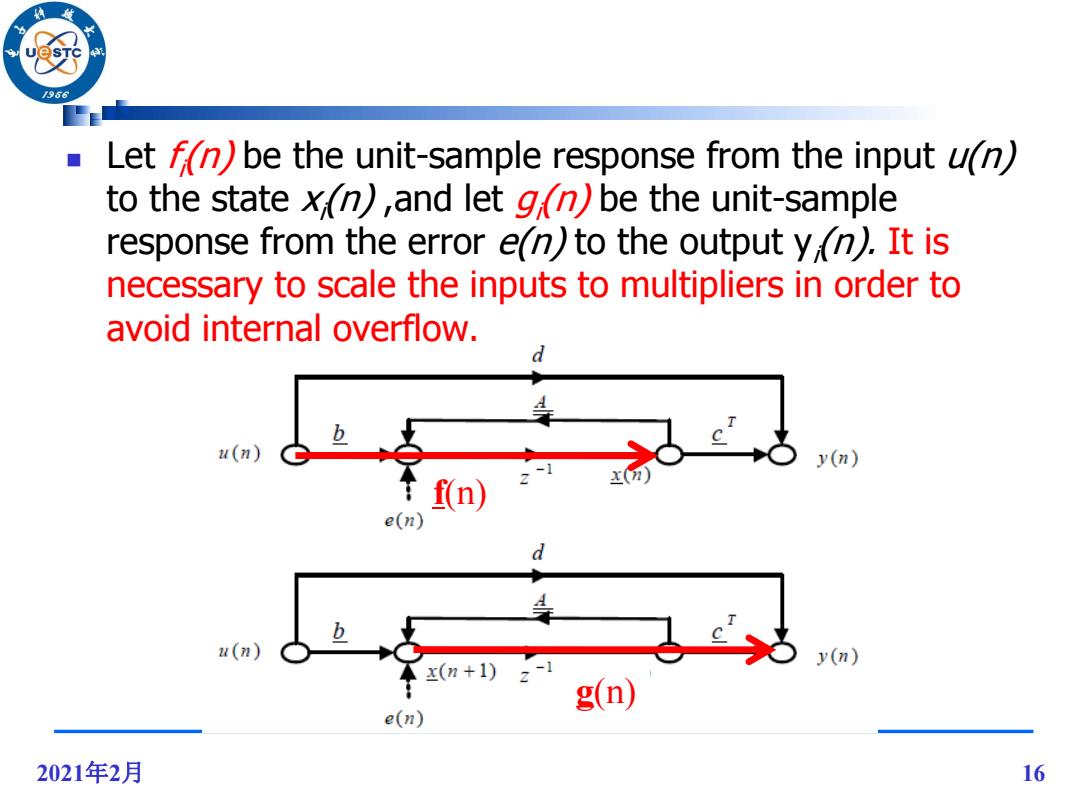
2021年2月 16 Let f i (n) be the unit-sample response from the input u(n) to the state xi (n) ,and let gi (n) be the unit-sample response from the error e(n) to the output yi (n). It is necessary to scale the inputs to multipliers in order to avoid internal overflow. f(n) g(n)

/966 Signals x(n)are input to the multipliers in Fig11.5.We need to compute f(n)for scaling. Conversely,to find the noise variance at the output,it is necessary to find the unit-sample response from the location of the noise source e(n)to y(n).Thus g(n) represents the unit-sample response of the noise transfer function except for a delay. 2021年2月 17
2021年2月 17 Signals x(n) are input to the multipliers in Fig11.5. We need to compute f(n) for scaling. Conversely, to find the noise variance at the output, it is necessary to find the unit-sample response from the location of the noise source e(n) to y(n). Thus g(n) represents the unit-sample response of the noise transfer function except for a delay

/96 十00 F(a)=∑fnz F(z)z-1dz n=-00 X(e) b21 (11.12) ve 0I-14 Then we can write the z-transform of f(n),F(z)as, Ea)=X(e)/W日)=+41+42:2+…b1, (11.13) =f0m)=4m-.b,n≥1. (11.14) ■ We can compute f(n)by substituting u(n)by 6(n)and using the recursion(11.15)and initial condition f(O)-0. f+1)=4f(m+bδ(0m) (11.15) 2021年2月 18
2021年2月 18 Then we can write the z-transform of f(n), F(z) as, We can compute f(n) by substituting u(n) by δ(n) and using the recursion (11.15) and initial condition f(0)=0
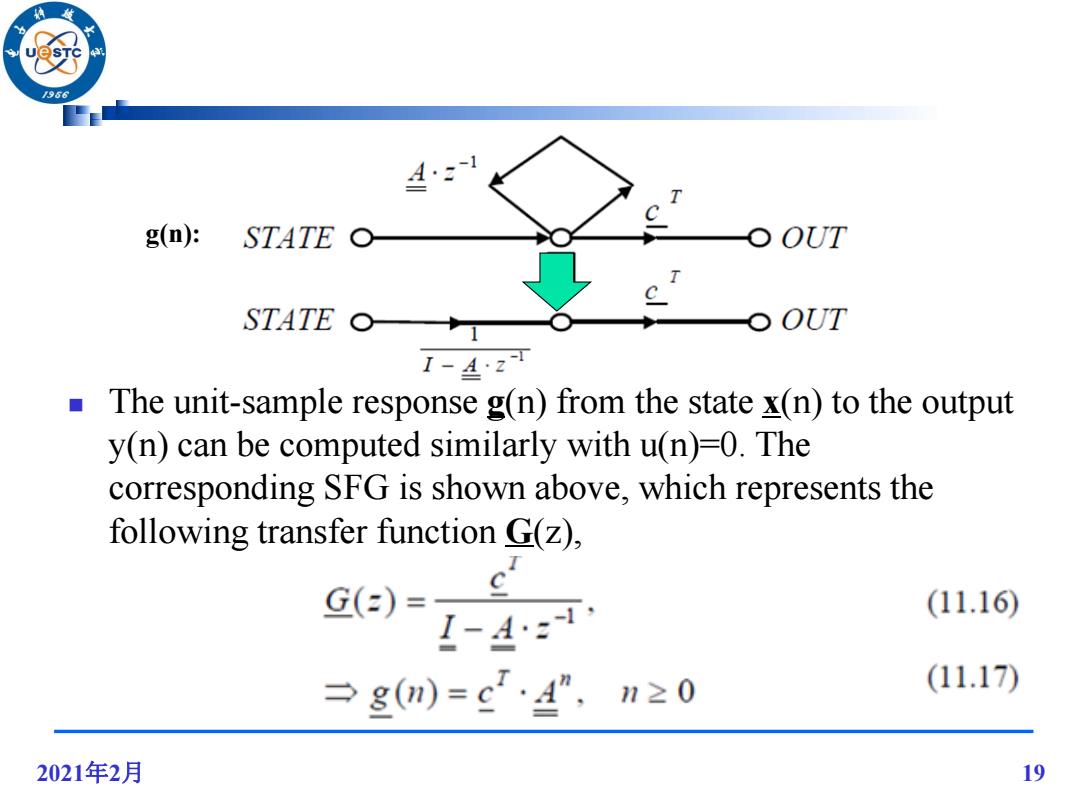
/966 g(n): STATE o OUT STATE O OUT 1-4z可 The unit-sample response g(n)from the state x(n)to the output y(n)can be computed similarly with u(n)-0.The corresponding SFG is shown above,which represents the following transfer function G(z), Ge)=1-4: (11.16) →g)=c·4",n≥0 (11.17) 2021年2月 19
2021年2月 19 The unit-sample response g(n) from the state x(n) to the output y(n) can be computed similarly with u(n)=0. The corresponding SFG is shown above, which represents the following transfer function G(z), g(n):