
The Branch-and-Bound Method Subproblem I t=1 = 6= 南24 24 与53 Subproblem 2 Subprohlem 2 2=4 12 =4 Subprubiem 3 1m2 新三4 Subproblem 3 =号 22 S 1 22 S I Subprobdem 4 13 t4 = Inteahle Subproblem 4 =3 【=4 =1 Infeasible = 3=1 25 4 525 TI S 4 Subproblem 6 Subprabiem 7 2=37 =4 :=1 Canddate solution )Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 11/42
The Branch-and-Bound Method Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 11 / 42

The Branch-and-Bound Method Definition 2.1 When further branching on a subproblem cannot yield any useful information,we say that the subproblem (or node)is fathomed. Definition 2.2 A solution obtained by solving a subproblem in which all variables have integer values is a candidate solution.The z-value for the candidate solution is a lower bound on the optimal z-value for the original IP. Definition 2.3 The LIFO(last in first out)approach,which chooses to solve the most recently created subproblem,is often called backtracking.When branching on a node,the jumptracking approach solves all the problems created by the branching.Then it branches again on the node with the best z-value. 0Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 12/42
The Branch-and-Bound Method Definition 2.1 When further branching on a subproblem cannot yield any useful information, we say that the subproblem (or node) is fathomed. Definition 2.2 A solution obtained by solving a subproblem in which all variables have integer values is a candidate solution. The z -value for the candidate solution is a lower bound on the optimal z -value for the original IP. Definition 2.3 The LIFO (last in first out) approach, which chooses to solve the most recently created subproblem, is often called backtracking. When branching on a node, the jumptracking approach solves all the problems created by the branching. Then it branches again on the node with the best z -value. Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 12 / 42
The Branch-and-Bound Method Suhproblem I f=1 1=1 4 = 24 ≤3 24 1s3 t2 。4 Subproblemn 2 Subprobicm 3 2=4 2=30 1=2 与“4 1=7 =3 22 的至1 台如号 =3 LB=40 22 5≤ Intasibie 23 4 t=3 Sabproblem 4 1=4 【nfeasible 1一帮 =1 2 37 1■4 6 =5 25 ±=0 I1 S 4 【M=32 Candilate olutson Subproblem 6 Subproblem 7 2=40 正”7 1=6 1=5 f=5 【1=4 中 杜0 Candictate solution Candidate solution 0Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 13/42
The Branch-and-Bound Method Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 13 / 42

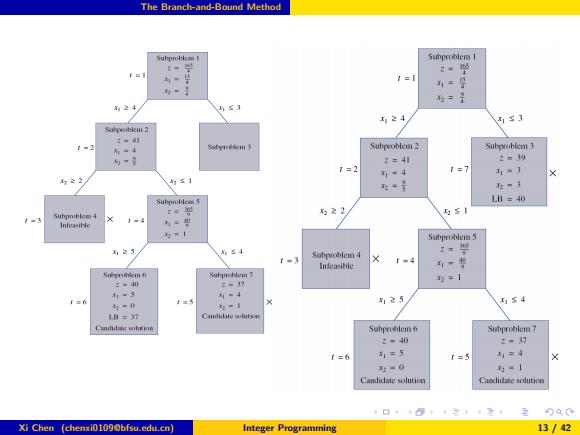
The Branch-and-Bound Method The key aspects of the branch-and-bound method for solving pure IPs may be summarized as follows: Step 1 If it is unnecessary to branch on a subproblem,then it is fathomed. The following three situations result in a subproblem being fathomed: (1)The subproblem is infeasible: (2)the subproblem yields an optimal solution in which all variables have integer values;and (3)the optimal z-value for the subproblem does not exceed (in a max problem)the current LB. Step 2 A subproblem may be eliminated from consideration in the following situations: (1)The subproblem is infeasible(in the Telfa problem,subproblem 4 was eliminated for this reason); (2)the LB(representing the z-value of the best candidate to date)is at least as large as the z-value for the subproblem(in the Telfa problem,subproblems 3 and 7 were eliminated for this reason). DaO Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 14/42
The Branch-and-Bound Method The key aspects of the branch-and-bound method for solving pure IPs may be summarized as follows: Step 1 If it is unnecessary to branch on a subproblem, then it is fathomed. The following three situations result in a subproblem being fathomed: (1) The subproblem is infeasible; (2) the subproblem yields an optimal solution in which all variables have integer values; and (3) the optimal z-value for the subproblem does not exceed (in a max problem) the current LB. Step 2 A subproblem may be eliminated from consideration in the following situations: (1) The subproblem is infeasible (in the Telfa problem, subproblem 4 was eliminated for this reason); (2) the LB (representing the z-value of the best candidate to date) is at least as large as the z-value for the subproblem (in the Telfa problem, subproblems 3 and 7 were eliminated for this reason). Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 14 / 42