
的初始储能产生的响应,它是电路的齐次微分方程满住初试条件的解。若零输入响应用 ∫)表示,其初始值为f(0,),则零输入响应可表示为 L.()=1(0.)e t>0 上式可以作为公式直接应用如本题的求解。 7-4 开关S原在位置1己久,t0时合向位置2,求c()和()。 1 100k2 -100k2 10μF 解:1>0时的电路如题解7-4图(a)所示。 25Q2 ①5w 1002 uc(0_) 100a 104F (a) (b) 题解6.4图 由图可知 5 .0.)=100+25×100=4 故可得电容电压的初始值 4c(0,)=(0.)=4 1>0后的电路如题解图(b)所示,这是一个一阶RC零输入电路。由于从电容两端看去的等效电阻 为R=100∥100=50k2 故有时间常数r=RC=50x10×10x10=之9 电容电压 uc(t)=uc(0.)e :=4e-2V 电流 0=9-0o4em4
的初始储能产生的响应,它是电路的齐次微分方程满住初试条件的解。若零输入响应用 f (t) x 表示,其初始值为 (0 ) x + f ,则零输入响应可表示为 t x x f t f e = + ( ) (0 ) t 0 上式可以作为公式直接应用如本题的求解。 7-4 开关 S 原在位置 1 已久,t=0 时合向位置 2,求 u (t) C 和 i(t) 。 + 5V 25k 100k + uc 10F 1 2 S 100k i 解:t > 0 时的电路如题解 7-4 图(a)所示。 由图可知 uC 100 4V 100 25 5 (0 ) = + = 故可得电容电压的初始值 uC (0+ ) = uC (0 ) = 4V t > 0 后的电路如题解图(b)所示,这是一个一阶 RC 零输入电路。由于从电容两端看去的等效电阻 为 R0 =100//100 = 50k 故有时间常数 R C s 2 1 50 10 10 10 3 6 = 0 = = 电容电压 u t u e e V t t C C 2 ( ) (0 ) 4 = + = 电流 e mA u t i t C 2t 0.04 100 ( ) ( ) = =

7-5 图中开关S在位置1已久,1=0时合向位置2,求换路后的i(t)和4,(t)。 12 +wL- ①10v 42 42 题6-5图 解:1>0时的电路如题图解(a)所示。 由图(a)可知 10 0)=+424 根据换路时i,不能跃变,有 i(0.)=i(0.)=2A >0后的电路如图(b)所示。这是一个一阶RL零输入电路。其时间常数为 L11 7=R4+489 故电感电流和电压分别为 i(t)=i(t)=i(0.)e=2eA 4,0=L亚=1x2e"x-8)=-16e*p d 也可利用KVL计算u,(),即 4()=-(4+4),()=-16ev 注:从7-3到75题的求解过程可以归纳出一阶电路零输入响应的步骤为:(1)由1=0的电路确定 电容电压4c(0)或1,(0_)电感电流,根据c(0,)=4c(0),z(0)=z(0)得出动态元件的初始值: ②)求1>0后电路的时间常数T,对RC电路有T=RC,对RL电路有7,式中飞为动态 元件两端看去的一端口电路的等效电阻,计算R,的方法与求戴维宁等效电阻的方法相同:(3)利用 c(I)=ue(0,)er或i,()=iz(0,)er,求得4e()和i,),再利用KCL或KL元件的伏安关系
7-5 图中开关 S 在位置 1 已久,t = 0 时合向位置 2,求换路后的 i(t) 和 u (t) L 。 解:t > 0 时的电路如题图解(a)所示。 由图(a)可知 i L 2A 1 4 10 (0 ) = + = 根据换路时 L i 不能跃变,有 i L (0+ ) = i L (0 ) = 2A t>0 后的电路如图(b)所示。这是一个一阶 RL 零输入电路。其时间常数为 s R L 8 1 4 4 1 = + = = 故电感电流和电压分别为 i t i t i e e A t t L L 8 ( ) ( ) (0 ) 2 = = + = e e V dt di u t L L t t L 8 8 ( ) 1 2 ( 8) 16 = = = 也可利用 KVL 计算 u (t) L ,即 8 ( ) (4 4) ( ) 16 t L L u t i t e V = + = 注:从 7-3 到 7-5 题的求解过程可以归纳出一阶电路零输入响应的步骤为:(1)由 t 0 = 的电路确定 电容电压 (0 ) C u 或 (0 ) L i 电感电流,根据 (0 ) C u + = (0 ) C u , (0 ) (0 ) L L i i + = 得出动态元件的初始值; (2)求 t 0 后电路的时间常数 。对 RC 电路有 R C0 = ,对 RL 电路有 0 L R = ,式中 R0 为动态 元件两端看去的一端口电路的等效电阻,计算 R0 的方法与求戴维宁等效电阻的方法相同;(3)利用 ( ) (0 ) t C C u t u e = + 或 ( ) (0 ) t L L i t i e = + ,求得 () C u t 和 () L i t ,再利用 KCL 或 KVL 元件的伏安关系

式求出其它各支路的电压和电流。也可根据0等效电路,求出其它待求量的初值,应用 ()=f(0.)er得到所求量 7-6 图示电路中,若0时开关S闭合,求电流1。 0.1H 20uF YY m 0.11 i 20F 1002 1002s〉 01002 11502 150g2 1002 60 60v 题7-6图 解:设t<0时,S打开且保持足够长的时间,因此,电路已达稳态,有L短路,C开路,见图7-5(a)。 .0) 4.(0.) 20μ 1502 100 :1009l 6( 1002 1502 ①60V 图7-5(a) 图7-5(b) 于是,由KVL定律i(0) 60 150+100=0,24A 4.(0_)=60V-150×i(0_)=60V-36V=24V 1=0时,S闭合,发生换路,电路如图7-5(b)所示,由换路定则有 i,(0)=i,(0)=0.24A,4.(0)=4.(0)=24V 由于短路,L和C分别组成互不相关的回路,因此,在1>0时,仍然为一阶零输入回路: RC回路:4.=4.(0,)e=24e0rV RL回路:1=,0,e兰-024emA 由于10=C,@20×10-×24×仁500y0mA=-0.24e0A d 因此,由KCL定律:i=-,()-i.()=0.24e6o-e-1omA 7-9 图示电路中,若1=0时开关S打开,求4和电源发出的功率
式求出其它各支路的电压和电流。也可根据 0+ 等效电路,求出其它待求量的初值,应用 ( ) (0 ) t x x f t f e = + 得到所求量 7-6 图示电路中,若 t=0 时开关 S 闭合,求电流 i。 + 100 150 60V 100 0.1H 20F S i 题 7-6 图 解:设 t<0 时,S 打开且保持足够长的时间,因此,电路已达稳态,有 L 短路,C 开路,见图 7-5(a)。 + 100 150 60V 100 ( ) ( ) u c 0 L 0 i + + 100 150 60V 100 0.1H 20F i u c L i c i 图 7-5(a) 图 7-5(b) 于是,由 KVL 定律 0.24A 150 100 60 (0 ) = + iL = uc (0 ) = 60V 150 iL (0 ) = 60V 36V = 24V t = 0 时, S 闭合,发生换路,电路如图 7-5(b)所示,由换路定则有 i L (0+ ) = i L (0 ) = 0.24A,uc (0+ ) = uc (0 ) = 24V 由于短路, L 和 C 分别组成互不相关的回路,因此,在 t 0 时,仍然为一阶零输入回路: RC 回路: (0 ) 24 V RC 500t t c c u u e e = + = RL 回路: (0 ) 0.24 A 1000t t L R L L i i e e = + = 由于 ( ) 20 10 24 ( 500) A 0.24 A ( ) c 6 500t 500t c e e dt du t i t C = = 因此,由 KCL 定律: ( ) ( ) 0.24( )A 500t 1000t L c i i t i t e e = = 7-9 图示电路中,若 t = 0 时开关 S 打开,求 C u 和电源发出的功率
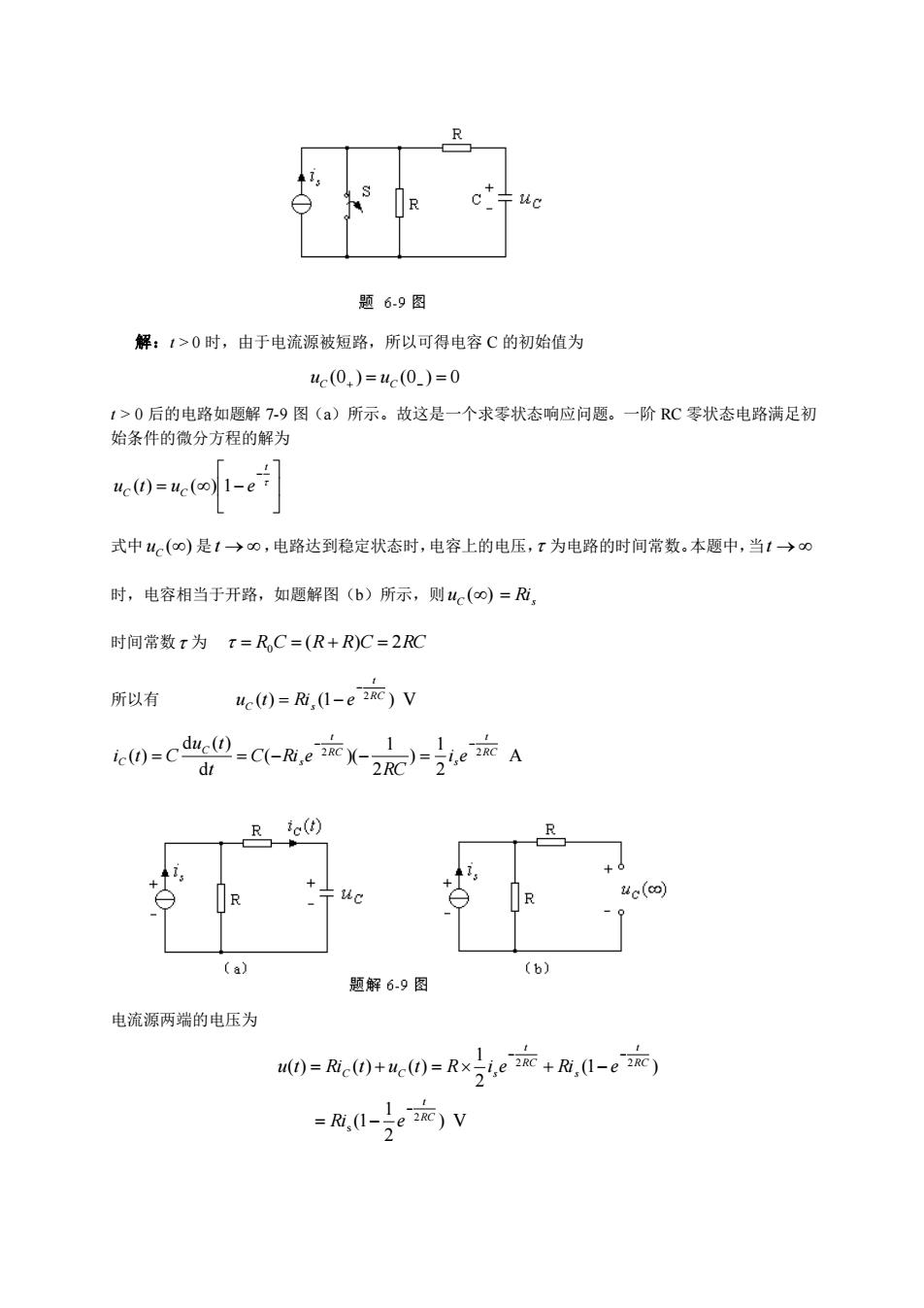
cT卡uc 题6-9图 解:1>0时,由于电流源被短路,所以可得电容C的初始值为 c(0,)=4c(0)=0 1>0后的电路如题解7-9图()所示。故这是一个求零状态响应问愿。一阶RC零状态电路满足初 始条件的微分方程的解为 4e0=e(m1-e] 式中4c(0)是t→0,电路达到稳定状态时,电容上的电压,t为电路的时间常数。本题中,当1→0 时,电容相当于开路,如题解图(b)所示,则4(o)=, 时间常数t为T=RC=(R+R)C=2RC 所以有 uc(t)=Ri,(1-eZRC)V 0=c-C-e产X-)e产A dt +0 R R uc(co) 〔a) (b) 题解6-9图 电流源两端的电压为 0=风e0+e0=Rx之,e壶+危,0-e)
解:t > 0 时,由于电流源被短路,所以可得电容 C 的初始值为 uC (0+ ) = uC (0 ) = 0 t > 0 后的电路如题解 7-9 图(a)所示。故这是一个求零状态响应问题。一阶 RC 零状态电路满足初 始条件的微分方程的解为 = t C C u (t) u ( ) 1 e 式中 () uC 是 t → ,电路达到稳定状态时,电容上的电压, 为电路的时间常数。本题中,当 t → 时,电容相当于开路,如题解图(b)所示,则 () uC = Ris 时间常数 为 = R0C = (R + R)C = 2RC 所以有 ( ) (1 2RC ) V t C s u t Ri e = A 2 1 ) 2 1 ( )( d d ( ) ( ) 2 2RC t s RC t s C C i e RC C Ri e t u t i t C = = = 电流源两端的电压为 ) V 2 1 (1 (1 ) 2 1 ( ) ( ) ( ) 2 s 2 2 RC t RC t s RC t C C s Ri e u t Ri t u t R i e Ri e = = + = +
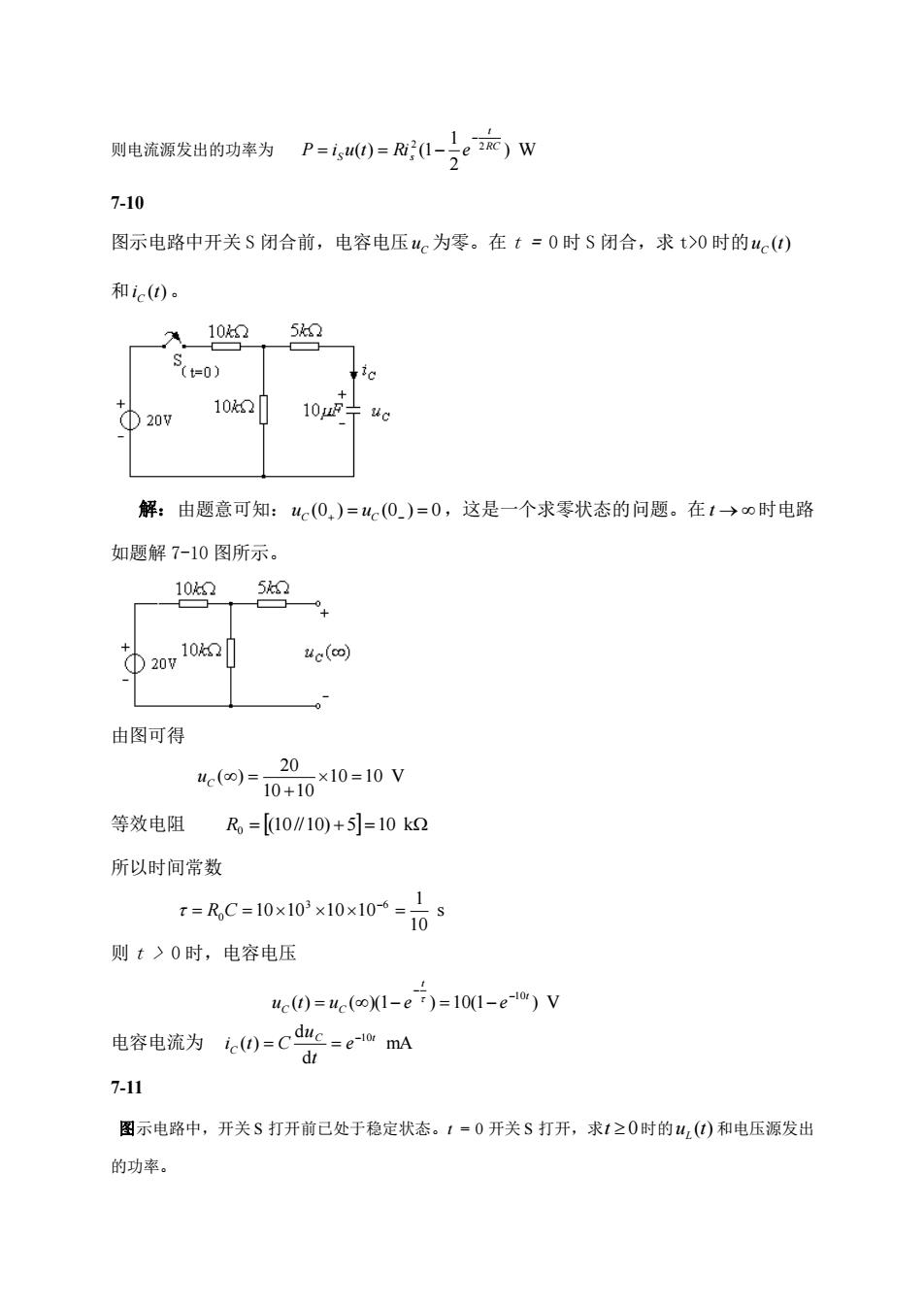
则电流返发出的功率为P=,)=0-)e证)W 7-10 图示电路中开关S闭合前,电容电压c为零。在t=0时S闭合,求t)0时的c() 和ie(0 10k2 5 (t=0) 102 209 10zF÷4c 解:由题意可知:4(0)=Wc(0.)=0,这是一个求零状态的问题。在1→o时电路 如题解7-10图所示。 102 52 4c(o) 由图可得 20 4e.(o)=10+10×10=10V 等效电阻R。=[10/10)+5]=10k2 所以时间常数 RC-10x10x10x10 则t>0时,电容电压 4e(0=ae(ol-ei)=101-e")V 电容电流为0=C普=e”A 7-11 图示电路中,开关S打开前己处于稳定状态。1-0开关S打开,求1之0时的4,)和电压源发出 的功率
则电流源发出的功率为 ) W 2 1 ( ) (1 2 2RC t S s P i u t Ri e = = 7-10 图示电路中开关 S 闭合前,电容电压 C u 为零。在 t = 0 时 S 闭合,求 t>0 时的 u (t) C 和 i (t) C 。 解:由题意可知: uC (0+ ) = uC (0 ) = 0 ,这是一个求零状态的问题。在 t → 时电路 如题解 7-10 图所示。 由图可得 10 10 V 10 10 20 ( ) = + uC = 等效电阻 R0 = (10//10) + 5=10 k 所以时间常数 s 10 1 10 10 10 10 3 6 = 0 = = R C 则 t > 0 时,电容电压 ( ) ( )(1 ) 10(1 ) V 10t t C C u t u e e = = 电容电流为 mA d d ( ) C 10t C e t u i t C = = 7-11 图示电路中,开关 S 打开前已处于稳定状态。t = 0 开关 S 打开,求 t 0 时的 u (t) L 和电压源发出 的功率