
第4章电路定理 4-1 应用叠加定理求图示电路中电压W6。 1 22 A 329 12/ 题4-图 22 12 22 ①5 sinty 32 120 32e 12 (d 题解4-图 解:首先画出两个电源单独作用式的分电路入题解41图(a)和(b)所示。 对(a)图应用结点电压法可得 1 解得 aSin3sint V 8-1-3m=sm:y 2+1 对(b)图,应用电阻的分流公式有 i=- +动+1359 所以 8=lx1=写e=02ey 故由叠加定理得 uab =ud+u=sint+0.2e V 12 22 12 29 32 12 32 12 () 题解4-图
第 4 章 电路定理 4-1 应用叠加定理求图示电路中电压 ab u 。 解:首先画出两个电源单独作用式的分电路入题解 4-1 图(a)和(b)所示。 对(a)图应用结 点电 压 法可 得 1 5sin ) 2 1 1 3 1 (1 1 t un = + + + 解得 1 5sin 3sin 5 3 n t u t V = = (1) 1 1 1 1 1 3sin sin 2 1 3 3 n ab n u u u t t V = = = = + 对(b)图,应用 电阻 的 分流 公 式有 1 1 3 2 1 1 1 1 3 5 t e t i e A − − + = = + + 所以 (2) 1 1 0.2 5 t t ab u i e e V − − = = = 故由叠加定理得 (1) (2) sin 0.2 t ab ab ab u u u t e V − = + = +
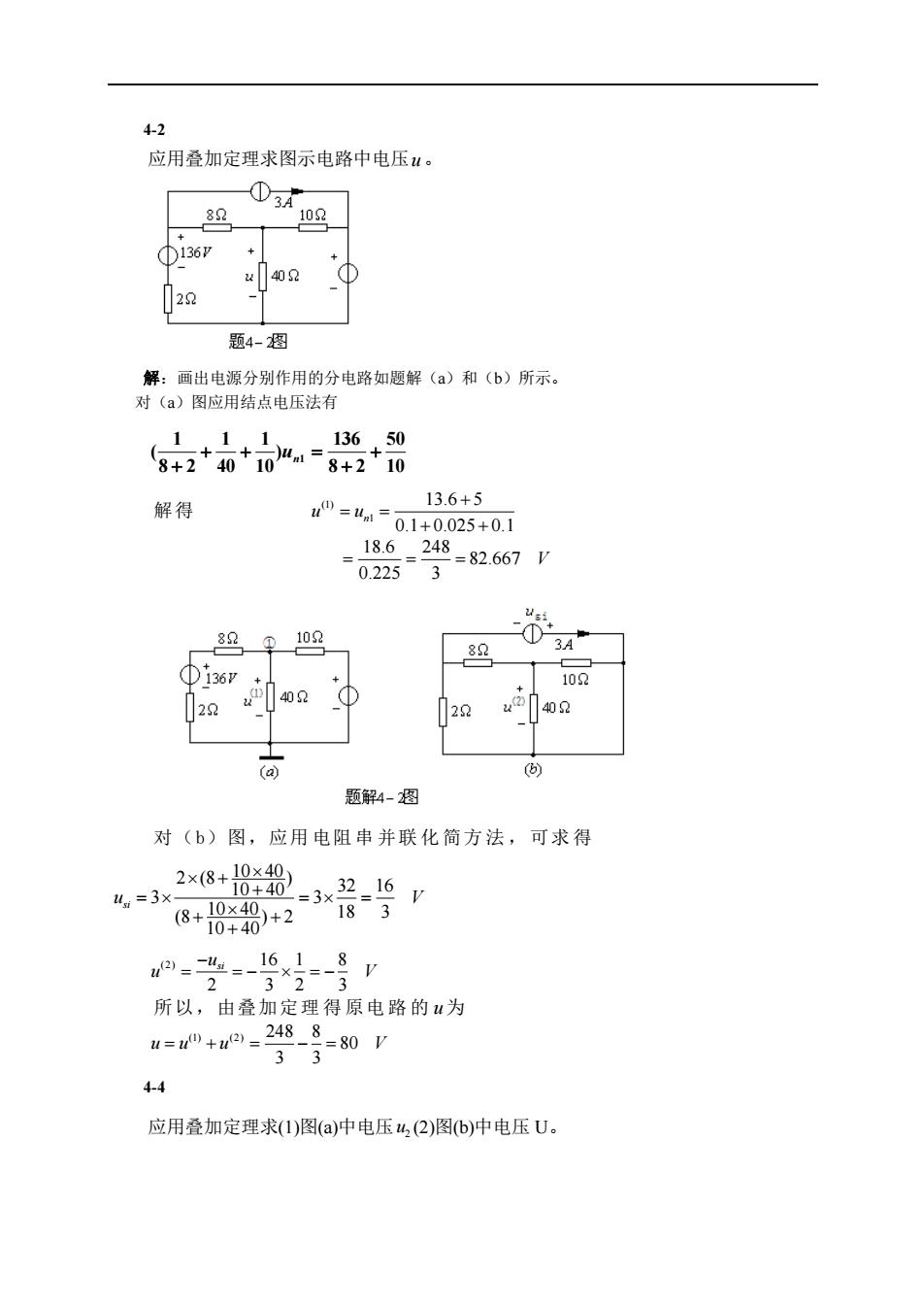
42 应用叠加定理求图示电路中电压。 -①3 82 109 ①136p 29 题4-图 解:画出电源分别作用的分电路如题解(a)和(b)所示。 对(a)图应用结点电压法有 +0 1 1 1 解得 13.6+5 49=-0.1+0.025+01 18.6248 =82.667V 02253 82 34 ①i36v 102 20 402 22 40 题解4-2图 对(b)图,应用电阻串并联化简方法,可求得 2×8+8¥0」 a=3 8+1840)+2 09r 所以,由叠加定理得原电路的“为 u=0+w9=248-8=80y 331 44 应用叠加定理求(1)图(a)中电压4,(2)图b)中电压U
4-2 应用叠加定理求图示电路中电压 u 。 解:画出电源分别作用的分电路如题解(a)和(b)所示。 对(a)图应用结点电压法有 10 50 8 2 136 ) 10 1 40 1 8 2 1 ( 1 + + + + = + un 解得 (1) 1 13.6 5 0.1 0.025 0.1 n u u + = = + + 18.6 248 82.667 0.225 3 = = = V 对(b)图,应用 电阻 串 并联 化 简方 法 , 可求 得 10 40 2 (8 ) 10 40 32 16 3 3 (8 ) 2 10 40 18 3 10 40 si u V + + = = = + + + (2) 16 1 8 2 3 2 3 si u u V − = = − = − 所以,由叠加定理得原电路的 u 为 (1) (2) 248 8 80 3 3 u u u V = + = − = 4-4 应用叠加定理求(1)图(a)中电压 2 u (2)图(b)中电压 U
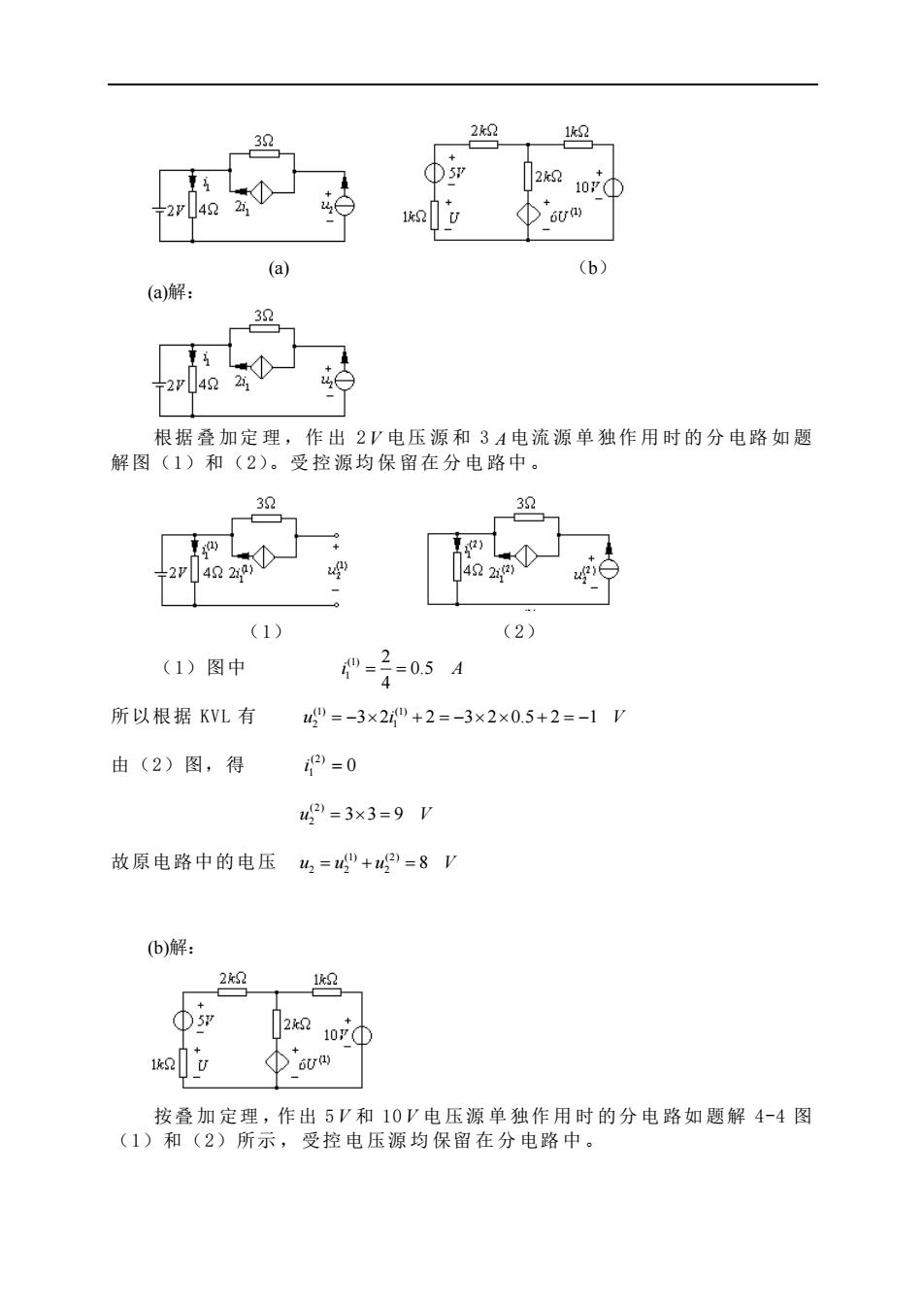
6t) (a) (b) (a)解 根据叠加定理,作出2V电压源和3A电流源单独作用时的分电路如题 解图(1)和(2)。受控源均保留在分电路中。 30 (1) (2) (1)图中 所以根据KVL有 "=-3×20+2=-3×2×0.5+2=-1V 由(2)图,得 2=0 42-3×3-9V 故原电路中的电压,=+2=8V b)解 2 小5 121o① 按叠加定理,作出5V和10V电压源单独作用时的分电路如题解4-4图 (1)和(2)所示,受控电压源均保留在分电路中
(a) (b) (a)解: 根据 叠 加定 理 ,作 出 2 V 电压 源 和 3 A 电流 源 单 独作 用 时的 分 电路 如 题 解图(1)和(2)。受 控 源均 保 留在 分 电 路中 。 (1) (2) (1)图中 (1) 1 2 0.5 4 i A = = 所以根据 KVL 有 (1) (1) 2 1 u i V = − + = − + = − 3 2 2 3 2 0.5 2 1 由(2)图,得 0 (2) i 1 = (2) 2 u V = = 3 3 9 故原电路中的电压 (1) (2) 2 2 2 u u u V = + = 8 (b)解: 按叠 加 定理 ,作出 5 V 和 10 V 电 压源 单 独作 用 时 的分 电 路如 题解 4-4 图 (1)和(2)所示 , 受控 电 压源 均 保留 在 分 电路 中
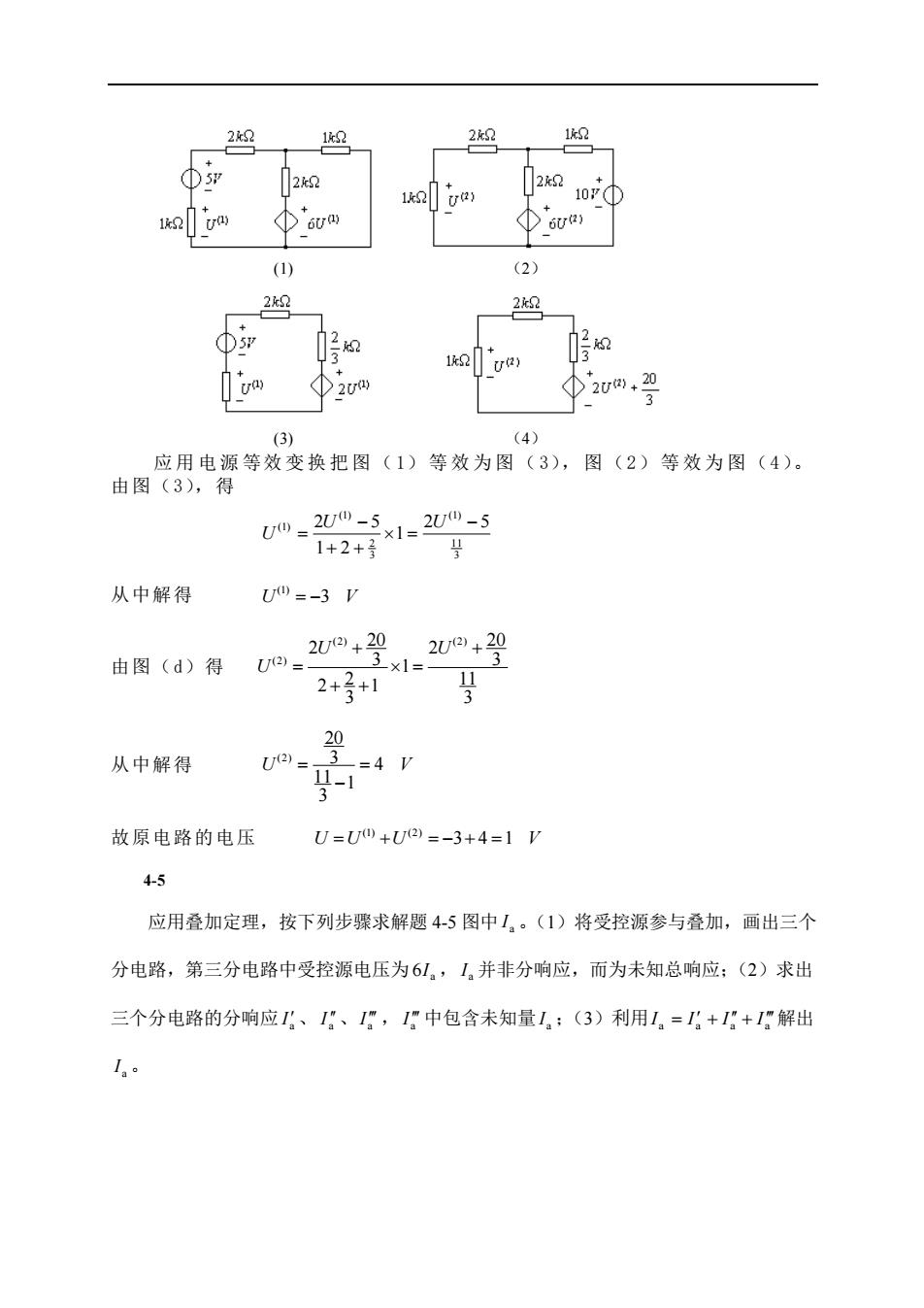
2 22 2k (2) 2 ①5 '2w, 3) (4) 应用电源等效变换把图(1)等效为图(3),图(2)等效为图(4) 由图(3),得 Uw-2w"-5 1=2Um-5 1+2+子1 从中解得 U0=-3V 0.2U+29 2w+29 由图(d)得 1 2++1 3 20 从中解得 U2= 4 故原电路的电压 U=U四+U2)=-3+4=1V 45 应用叠加定理,按下列步骤求解题4-5图中/,。(1)将受控源参与叠加,画出三个 分电路,第三分电路中受控源电压为61,1,并非分响应,而为未知总响应:(2)求出 三个分电路的分响应、1,1中包含未知量1:(3)利用1。=乃+:+I解出
(1) (2) (3) (4) 应 用 电 源 等效 变 换 把 图 ( 1)等效为图( 3), 图 (2)等效为图(4)。 由图(3),得 3 11 (1) 3 2 (1) (1) 2 5 1 1 2 2 5 − = + + − = U U U 从中解得 (1) U V = −3 由图(d)得 (2) (2) (2) 20 20 2 2 3 3 1 2 11 2 1 3 3 U U U + + = = + + 从中解得 (2) 20 3 4 11 1 3 U V = = − 故原电路的电压 (1) (2) U U U V = + = − + = 3 4 1 4-5 应用叠加定理,按下列步骤求解题 4-5 图中 a I 。(1)将受控源参与叠加,画出三个 分电路,第三分电路中受控源电压为 6 a I , a I 并非分响应,而为未知总响应;(2)求出 三个分电路的分响应 a I 、 a I、 a I , a I 中包含未知量 a I ;(3)利用 a a a a I = I + I + I 解出 a I
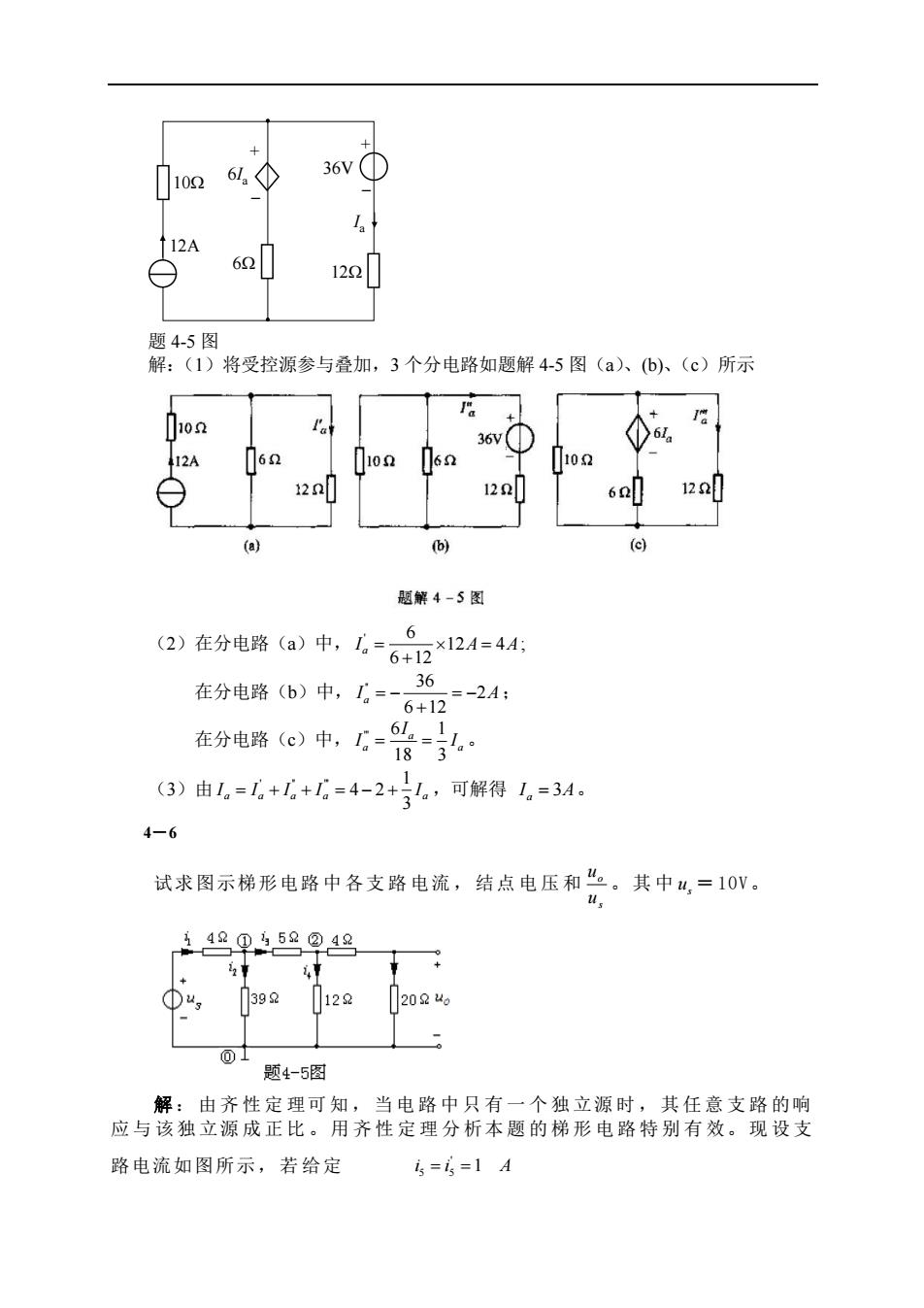
10261 36V 12A 62 122 题4-5图 解:(1)将受控源参与叠加,3个分电路如题解4-5图(a入、(b以、(c)所示 36v① 6 00 12 120 题解4-5图 6 2)在分电路(a)中,L-62×124=4 36 在分电路6)中,(=6521: 在分电路⊙)中,上-%· (3)由1,=1。+。+,=4-2+,可解得1,=3A。 4-6 试求图示梯形电路中各支路电流,结点电压和“。其中山,=10V 489.559②4鸟 392122024 ⑩士 题4-5图 解:由齐性定理可知,当电路中只有一个独立源时,其任意支路的响 应与该独立源成正比。用齐性定理分析本题的梯形电路特别有效。现设支 路电流如图所示,若给定 4=6=1A
+ − 6 I a 6I a + − 36V 10 12 12A 题 4-5 图 解:(1)将受控源参与叠加,3 个分电路如题解 4-5 图(a)、(b)、(c)所示 (2)在分电路(a)中, ' 6 12 4 6 12 a I A A = = + ; 在分电路(b)中, '' 36 2 6 12 a I A = − = − + ; 在分电路(c)中, ''' 6 1 18 3 a a a I I I = = 。 (3)由 ' '' ''' 1 4 2 3 a a a a a I I I I I = + + = − + ,可解得 3 a I A = 。 4-6 试求图示梯形电路中各支路电流,结点电压和 s o u u 。其中 s u = 10V。 解 : 由 齐 性 定 理可 知 , 当 电 路 中 只 有 一 个 独 立源 时 , 其 任 意 支 路 的响 应 与 该 独 立源 成 正 比 。 用 齐 性 定 理 分 析本 题 的 梯 形 电 路 特 别 有 效。 现 设 支 路电流如图所示,若给定 ' 5 5 i i A = =1