
第13章非正弦周期电流电路和信号的频谱 13-1 求下列非正弦周期函数∫()的频谱函数(傅里叶级数系数),并作频谱图。 (1)f(r)=cos4t+sin6t (2)f0如题13-1图(a、(b.(c)所示 f (a) 题13一1图f)的波形 13-2 设非正弦周期函数0的频谱函数为Ae=Q,一·试表述下列与f0相关函数的频谱函 数。 (1)f-o): 2)f0=f-). (3)f0=-f(-0, 4)f0=-f+12. 13-3 己知某信号半周期的波形如图所示。试在下列各不同条件下画出整个周期的波形: (1)a0=0,(2)对所有k,b=0,(3)对所有k,ak=,(4)a和bg为零,当k为偶数 时。 解:(1)当a。=0时,在后半个周期上,只要画出)的负波形与横轴(1轴)所围面积与
第 13 章 非正弦周期电流电路和信号的频谱 13-1 求下列非正弦周期函数 f t() 的频谱函数(傅里叶级数系数),并作频谱图。 (1) f t t t ( ) cos 4 sin 6 = + ; (2) f t() 如题 13—1 图(a)、(b)、(c)所示。 (a) (b) (c) f (t) f (t) f (t) Um - Um Um /2 - Um /2 O T/3 2T/3 T t - T/2 O T/2 t - T/2 T/2 -1 O 1 (t) t 题 13—1 图 f t() 的波形 13-2 设非正弦周期函数 f t() 的频谱函数为 j m j k A e a b k k k = − 。试表述下列与 f t() 相关函数的频谱函 数。 (1) 0 f t t ( ) − ; (2) f t f t ( ) ( ) = − ; (3) f t f t ( ) ( ) = − − ; (4) f t f t t ( ) ( / 2) = − + ; (5) d ( ) d f t t 。 13-3 已知某信号半周期的波形如图所示。试在下列各不同条件下画出整个周期的波形: (1)a 0 =0; (2) 对所有 k,b k =0;(3)对所有 k,a k =0;(4)a k 和 b k 为零,当 k 为偶数 时。 解:(1)当 a 0 =0 时,在后半个周期上,只要画出 f(t) 的负波形与横轴( t 轴)所围面积与
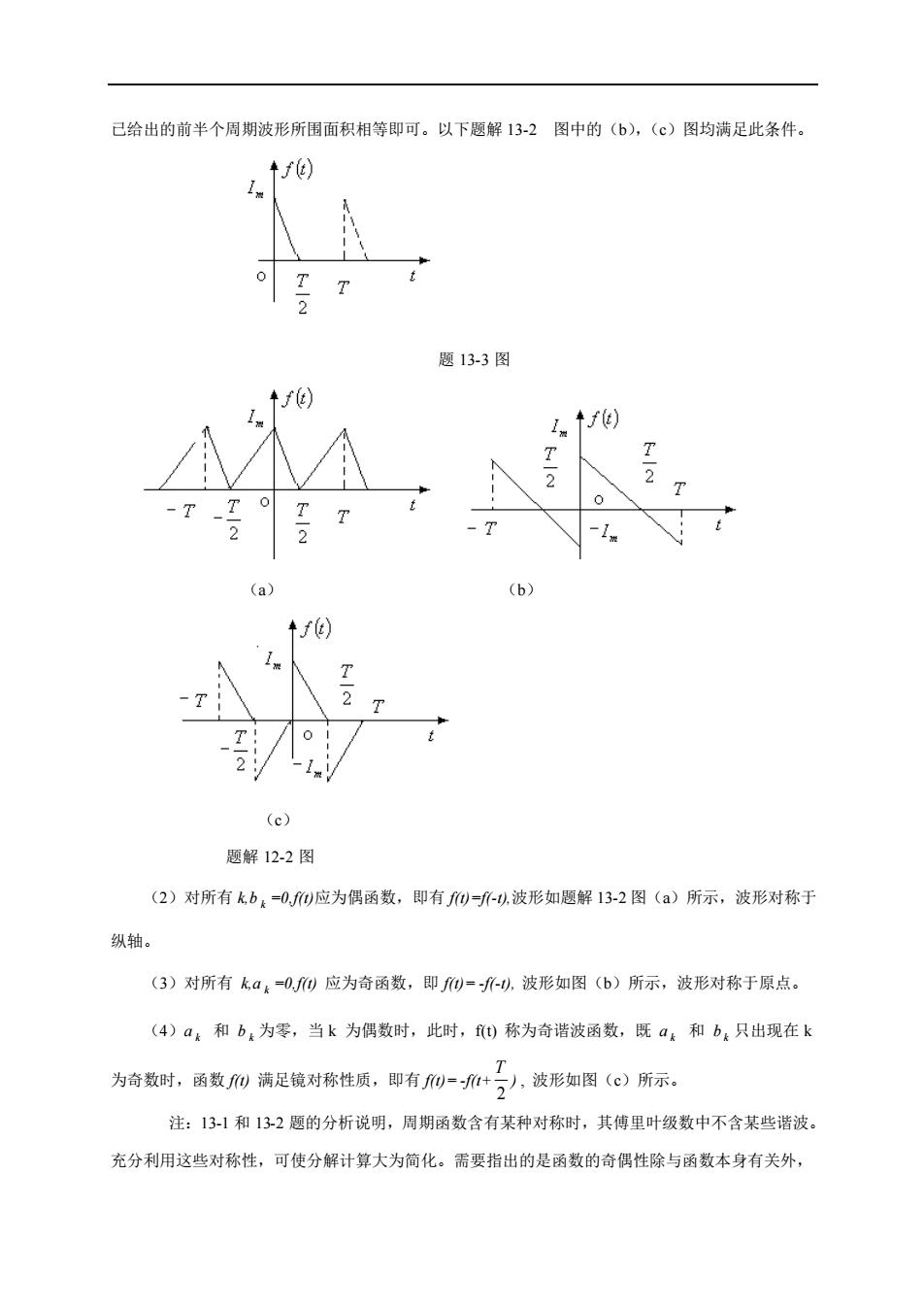
已给出的前半个周期波形所围面积相等即可。以下题解13-2图中的(b),(c)图均满足此条件。 ↑f) 题133图 +f) (a) (b) (c) 题解12-2图 (2)对所有kb,=0,)应为偶函数,即有)=升-.波形如题解13-2图(a)所示,波形对称于 纵轴。 (3)对所有ka:-00应为奇函数,即)=-,波形如图(b)所示,波形对称于原点。 (4)a:和b:为零,当k为偶数时,此时,f)称为奇谐波函数,既ak和bk只出现在k 为奇数时,函数m满足镜对称性质,即有们-了,波形如图(⊙)所示。 注:13-1和132题的分析说明,周期函数含有某种对称时,其傅里叶级数中不含某些谐波。 充分利用这些对称性,可使分解计算大为简化。需要指出的是函数的奇偶性除与函数本身有关外
已给出的前半个周期波形所围面积相等即可。以下题解 13-2 图中的(b),(c)图均满足此条件。 题 13-3 图 (a) (b) (c) 题解 12-2 图 (2)对所有 k,b k =0,f(t)应为偶函数,即有 f(t)=f(-t),波形如题解 13-2 图(a)所示,波形对称于 纵轴。 (3)对所有 k,a k =0,f(t) 应为奇函数,即 f(t)= -f(-t), 波形如图(b)所示,波形对称于原点。 (4)a k 和 b k 为零,当 k 为偶数时,此时,f(t) 称为奇谐波函数,既 a k 和 b k 只出现在 k 为奇数时,函数 f(t) 满足镜对称性质,即有 f(t)= -f(t+ 2 T ) , 波形如图(c)所示。 注:13-1 和 13-2 题的分析说明,周期函数含有某种对称时,其傅里叶级数中不含某些谐波。 充分利用这些对称性,可使分解计算大为简化。需要指出的是函数的奇偶性除与函数本身有关外

还与计时起点的选择有关,因此,对某些周期函数可以适当选择计时起点,使它成为奇函数或偶函 数,以便简化傅立叶级数的系数计算。 134 一个RLC串联电路。其R-12,L-0015H,C-704F,外加电压为 u)=1I+14L.4cos(1000w-35.4sin2000]V 试求电路中的电流)和电路消耗的功率。 解:RLC串联电路如题解133图所示,电路中的非正弦周期电压W)为已知,分别有直 流分量,基波和二次谐波分量。可写出电流相量的一般表达式 题解12-3图 U ZaR+aL-in 电压分量分别作用,产生的电流和功率分量为: (1)直流U。=1Ψ作用时,电感L为短路,电容C为开路,故,1。=0,P。=0。 (2)基波(k=)作用时,令U=100∠0°V Zw=RaL-6C)-10.714)n=1023∠37Ip 100∠0° 故1m会"n28T974-37入 P=IR=905.28W 2三次谐波k=2引作用时,令0心a=35490°25032∠90 ZaR20L-20C)-+00-号x1428%-25,36∠6430
还与计时起点的选择有关,因此,对某些周期函数可以适当选择计时起点,使它成为奇函数或偶函 数,以便简化傅立叶级数的系数计算。 13-4 一个 RLC 串联电路。其 R=11 ,L=0.015H ,C=70 F , 外加电压为 u(t) = [11+141.4cos(1000t) –35.4sin(2000t)]V 试求电路中的电流 i(t) 和电路消耗的功率。 解: RLC 串联电路如题解 13-3 图所示,电路中的非正弦周期电压 u(t) 为已知,分别有直 流分量,基波和二次谐波分量。可写出电流相量的一般表达式 ( ) ( ) ( ) ) 1 ( ( ) . . k C R j k L U Z U I k k k k + − = = 其中 , L =15 , C 1 =14.286 . 电压分量分别作用,产生的电流和功率分量为: (1) 直流 U0 =11V 作用时,电感 L 为短路,电容 C 为开路,故,I 0 =0 , P0 =0 。 (2) 基波 (k=1)作用时,令 . U =100 0 0 V Z (1) = R+j( L — C 1 ) =(11+j0.714) =11.023 0 3.71 故 (1) . I = (1) (1) Z U = 0 0 11.023 3.71 100 0 =9.072 0 − 3.71 A P (1) = I 2 (1) R = 905.28 W (3)二次谐波 (k=2) 作用时,令 U(2) = 0 90 2 35.4 =25.032 0 90 V Z (2) =R +j(2 L — 2C 1 ) =11 +j(30 — 2 1 14.286) =25.366 0 64.3

故1。0536264 .02=25.032∠90° =0.987∠25.7°A P=2R=0.98)2x11=10.716w 所以,电路中的电流10为 i(0=0+2x9.072cos(1000t-3.71°)+2×0.987co2000t+25.7) =12.83c0s(1000t-3.71)-1.396sin(2000t-64.3)A 电路消耗的功率 P-D+Po+P2=905.28+10.716=916W 13-5 电路如图所示,电源电压为 4s()=[50+100sin(314t)-40cos(628t)+10sin(942t+20°)JV 试求电流1)和电源发出的功率及电源电压和电流的有效植。 102 5020R s 01m504 题12-4图 题124国 解:设电流10第k次谐波的向量为(采用复振幅相量)。(1)当k-0,直流分量U= 50V作用时,电路如题解12-4图所示,有Z。=R+R1=602,故
故 (2) I = (2) (2) Z U = 0 0 25.366 64.3 25.032 90 = 0.987 0 25.7 A P (2) =I 2 (2) R =(0.98) 2 11 = 10.716 W 所以,电路中的电流 i (t) 为 i (t) = 0 + 2 9.072 cos (1000t — 3.71 0 ) + 2 0.987 cos(2000t + 25.7 0 ) = 12.83 cos (1000t - 3.71 0 ) – 1.396 sin (2000t – 64.3 0 ) A 电路消耗的功率 P = P0 + P(1) + P(2) = 905.28 +10.716 = 916 W 13-5 电路如图所示,电源电压为 S u (t) = [ 50 + 100 sin ( 314t ) – 40 cos (628t ) + 10 sin ( 942t + 20 0 )]V 试求电流 i (t) 和电源发出的功率及电源电压和电流的有效植。 解:设电流 i (t) 第 k 次谐波的向量为 m(k ) I (采用复振幅相量)。(1)当 k = 0 ,直流分量 U 0 = 50V 作用时,电路如题解 12-4 图所示,有 Z 0 =R +R 1 = 60 ,故

P。=U,-0g416w (2)当-l,即可=可,=314ads,基波向量00=100∠-90°V作用时,有 1 Z=10+j3.14+ -=71.267∠-19.31°2 00157+30+314 1 故 0n7267Z193=1403∠-7069A in Zo 100∠-90° x1.403c0193 =66.2W (3)当k-2,即0=2@,=628ds,二次谐波向量02=40∠0°V作用时,有 1 Z2=10+j6.28+ -=42.528∠-54.552°2 00314+30+j628 1 故 -40∠00 2=Z42.528∠-54.5520=09412-125448° Pe,=0✉g1ac0s-5452)=7×40x094xcos54.52°=10,915w (4)当k=3,即0=30,=942rad/s,三次谐波相量Usw6)=10∠-70p作用时,有 1 Z6=10+j9.42+ =20.552∠-51.192 0.0471+50+j942 故
I 0 = 0 0 Z U = 60 50 = 6 5 A P s0 = U 0 I 0 = 50 6 5 = 41.667 W (2)当 k=1 ,即 = 1 =314 rad s, 基波向量 Usm(1) = 100 0 − 90 V 作用时,有 Z (1) = 10 + j3.14 + 50 31.4 1 0.0157 1 j j + + = 71.267 0 −19.31 故 m(1) I = (1) (1) Z Usm = 0 0 71.267 19.31 100 90 − − = 1.403 0 − 70.69 A P s(1) = 2 1 0 0 (1) (1) 100 1.403cos19.31 2 1 Usm I m cos(−19.31 ) = =66.2 W (3)当 k=2 ,即 2 628rad s = 1 = , 二次谐波向量 0 Usm(2) = −400 V 作用时,有 Z = − + + = + + 0 (2) 42.528 54.552 50 62.8 1 0.0314 1 10 6.28 j j j 故 A Z U I sm m 0 0 0 (2) (2) (2) 0.941 125.448 42.528 54.552 40 0 = − − − = = (2) (2) 2 1 Ps = Usm I m 40 0.94 cos 54.552 10.915W 2 1 cos( 54.552 ) 0 0 (2) − = = (4)当 k=3,即 3 942rad s = 1 = ,三次谐波相量 U SM (3) =10 − 70V . 作用时,有 ( ) = − + + = + + 20.552 51.19 50 94.2 1 0.0471 1 3 10 9.42 j j Z j 故