
第14章线性动态电路的复频域分析 141求下列各函数的像函数: ()ft)=1-e (2)f(t)=sin(at+) (3)f=e(1-am) ④f0=上a-e) (⑤f)=t2 (6f0=1+2+36() (7)f(t)=tcos(at) (8)f()=e"+m-1 (2)F(s)=sin(ax+)=sin ax coso+cosarsinol aFo=iea-ml=c-ael=,ta4n产afa 4F=-=-e1=4 1 asa(s+a)ss+a) Fe)=P1=rreh=-rk=-号eg-子eg-子et-号 oF=4+2+3601=7++3 ona-ameI-时e4-o-网*orol品 1 s2-a2 (8)Fs)=5e"+at-1 1 142求下列各函数的原函数: )+s+3到 252+16 32+9+9 (s+2)(s+4) (2g+5s+6+12 s2+3s+2 (G+35+2 解:(1)设F(s)的部分分式展开为
第 14 章 线性动态电路的复频域分析 14-1 求下列各函数的像函数: at f t e − (1) ( ) = 1 − (2) f (t) = sin(t + ) (3) f (t) e (1 at) at = − − (1 ) 1 (4) ( ) at e a f t − = − 2 (5) f (t) = t (6) f (t) = t + 2 + 3δ(t) (7) f (t) = t cos(at) (8) ( ) = + − 1 − f t e at at 解: (1) ( ) [1 ] at F s e − = − ( ) 1 1 s s a a s s a + = + = − (2)F(s) = [sin(t + )] = [sint cos + costsin] 2 2 2 2 2 2 cos sin cos sin + + = + + + = s s s s s (3)F(s) [e (1 at)] at = − − [ ] at at e ate − − = − 2 2 ( ) ( ) 1 s a s s a a s a + = + − + = (1 )] 1 (4) ( ) [ at e a F s − = − ] 1 1 [ at e a a − = − ( ) 1 ( ) 1 1 as a s a s s + a = + = − (5) ( ) = [ ] = 2 F s t t e dt st − = 0 2 st t de s − = − 0 1 2 − − − = − 0 − 2 0 − 3 0 2 st 2 st 2 st te s te s e s t 3 2 s = (6)F(s) = [t + 2 + 3 (t)] 3 1 2 2 = + + s s (7)F(s) = [t cos(at)] ( )] 2 1 [ j t j t t e e − = + ] ( ) 1 ( ) 1 [ 2 1 2 2 s ja s + ja + − = 2 2 2 2 2 (s a ) s a + − = (8) ( ) = [ + − 1] − F s e at at s s a s a 1 1 2 + − + = ( ) 2 2 s s a a + = 14-2 求下列各函数的原函数: ( 2)( 4) ( 1)( 3) (1) + + + + s s s s s ( 5 6)( 12) 2 16 (2) 2 2 + + + + s s s s 3 2 2 9 9 (3) 2 2 + + + + s s s s s s s s ( 3 2) (4) 2 3 + + 解:(1)设 F(s) 的部分分式展开为

F回)=+5+).人+K:+K s(s+2)(s+4) +2++4 K,F 则待定系数为K,=(s+2)F一=4 K=lc+4FGl一号 所以,原函数为 0=0+2e*+3c) 2因为F-a+2*西-车+4名+车品 2s2+16 则待定系数为 k=c+3Fo-号 a 所以,有f0=是e”-。*+1是em 5 9 45 (3》因为F6=2+9灯+9=2+ 35+5 s2+3s+2 235+2 设F(d)为 =07产车+车 35+5 则待定系数为 k=c+ol-t2-2 K2=s+2)F(s川2= 35+5, 5+221 所以,原函数为f)=28)+2e+e 3 52 35+2 (④)因为F6)=G+35+2s=g子+35+21G+iW5+习
( 2)( 4) ( 1)( 3) ( ) + + + + = s s s s s F s 2 4 1 2 3 + + + = + s K s K s K 则待定系数为 8 3 [( 4) ( )] 4 1 [( 2) ( )] 8 3 [ ( )] 3 4 2 2 1 0 = + = = + = = = =− =− = s s s K s F s K s F s K sF s 所以,原函数为 (3 2 3 ) 8 1 ( ) 3t 4t f t e e − − = + + (2)因为 ( 2)( 3)( 12) 2 16 ( ) 2 + + + + = s s s s F s 2 3 12 1 2 3 + + + + + = s K s K s K 则待定系数为 45 152 [( 12) ( )] 9 34 [( 3) ( )] 5 12 [( 2) ( )] 3 12 2 3 1 2 = + = = + = − = + = =− =− =− s s s K s F s K s F s K s F s 所以,有 t t t f t e e e 2 3 12 45 152 9 34 5 12 ( ) − − − = − + (3)因为 3 2 2 9 9 ( ) 2 2 + + + + = s s s s F s 3 2 3 5 2 2 + + = + s s s 设 ( ) 1 F s 为 3 2 3 5 ( ) 1 2 + + + = s s s F s ( 1)( 2) 3 5 + + + = s s s 1 2 1 2 + + + = s K s K 则待定系数为 1 2 3 5 [( 2) ( )] 2 2 3 5 [( 1) ( )] 2 1 2 2 1 1 1 1 = + + = + = = + + = + = =− =− =− =− s s s s s s K s F s s s K s F s 所以,原函数为 t t f t t e e 2 ( ) 2 ( ) 2 − − = + + (4)因为 s s s s F s ( 3 2) ( ) 2 3 + + = ( 1)( 2) 3 2 1 3 2 2 2 + + + − + + = s s s s s s

设FS)为 3g+2 F(s)= (+105+2)s+1+2 则代定系数为 ,=5+0Fs=3s+2 5+2=-1 =5+2F6=3+2 所以,原函数为f)=)+e‘-4e 14-3求下列各函数的原函数: 1 (1) +1 (5+10s+2)2 ②+2+2 3)产+6s+5 s(s2+4s+5 ④G+1 解:(1)令D(s)=0,有P=-1为单根,P2=-2为二重根,所以,设发F9s)为 r0=a+W2点+号+o 1 用6+2乘以F刊得+2F)=,中 则代定系数为 k-+F()(2-1 k=- kagr 所以,原函数为f)=e-e-1e S+1 +1 《2)因为F)+2x+2G2+25+2D0 令Ds)=0有A=0为单根,A=-1+LP2=-1-1为共轭复根,所以,设 F)=+ K2+ K3 s5+1-js+1+1 则各系数为
设 ( ) 1 F s 为 ( 1)( 2) 3 2 ( ) 1 + + + = s s s F s 1 2 1 2 + + + = s K s K 则代定系数为 4 1 3 2 [( 2) ( )] 1 2 3 2 [( 1) ( )] 2 1 2 2 1 1 1 1 = + + = + = = − + + = + = =− =− =− =− s s s s s s K s F s s s K s F s 所以,原函数为 t t f t δ t e e 2 ( ) ( ) 4 − − = + − 14-3 求下列各函数的原函数: (1) 2 ( 1)( 2) 1 s + s + (2) s s s s 2 2 1 3 2 + + + (3) ( 4 5) 6 5 2 2 + + + + s s s s s (4) 2 2 (s + 1) s 解: (1)令 D(s) = 0, 有 p1 = −1 为单根, p2 = −2 为二重根,所以,设发 F9s) 为 2 1 22 21 2 ( 1)( 2) 1 2 ( 2) 1 ( ) + + + + + = + + = s K s K s K s s F s 用 2 (s + 2) 乘以 F(s) 得 1 1 ( 2) ( ) 2 + + = s s F s 则代定系数为 1 1 1 1 1 1 1 ( 2) 1 [( 1) ( )] 22 2 21 2 1 1 2 1 = − + = = − + = = + = + = =− =− =− =− s s s s ds s d K s K s K s F s 所以,原函数为 t t t f t e e te 2 2 ( ) − − − = − − (2)因为 ( ) 1 ( 2 2) 1 2 2 1 ( ) 3 2 2 D s s s s s s s s s s F s + = + + + = + + + = 令 D(s)=0 有 p1 = 0 为单根 , p1 = −1+ j1, p2 = −1− j1 为共轭复根,所以,设 1 1 1 ( ) 1 2 3 s j K s j K s K F s + + + + − = + 则各系数为

lF(05 k-28w云p03 s+1 K,=Ke4=03536en 所以,原函数为f)=0.5+0.707ecos1-135) (3)令D)=0有乃=0为单根,P2=-2+1P,=-2-1为共轭复根,设 F(s)= 产+65-+2-n+2* K2 K s2+45+5)3 则各系数为 k.-tru 人器n护等 K=Kke网=e5 所以,原函数为f)=1+2esnt (4因为F)=G++产s-)D) 令Ds)=0,有P=-j和P2=j分别为二重根,且P,和P2为共轭复根,故设 K. 则各系数为 =s+n“an-分-e K=Kk=e9-月 Ka=4【s+Fs-1=0 K2=0 所以,原函数为f0=J分e”-e=2sn1 144 图(a),(b),(c)所示电路原己达到稳态,=0时把开关S合上,分别画出运算电路
0 2 0 2 135 3 2 135 2 2 1 1 1 0 2 0 0.3536 0.3536 3 4 2 1 ( ) ( ) 0.5 2 2 1 [ ( )] j j j s p s j s s K K e e e s s s D s N s K s s s K sF s = = = + + + = = = + + + = = − − = =− + = = 所以,原函数为 ( ) 0.5 0.707 cos( 135 ) 0 = + − − f t e t t (3)令 D(s) = 0 有 p1 = 0 为单根, p2 = −2 + j1, p3 = −2 − j1 为共轭复根,设 ( 4 5) 2 1 2 1 6 5 ( ) 1 2 3 2 2 s j K s j K s K s s s s s F s + + + + − = + + + + + = 则各系数为 2 3 2 2 2 2 1 2 2 2 0 2 1 0 2 2 3 8 5 6 5 ( ) ( ) 1 4 5 6 5 [ ( )] j j j s p s j s s K K e e j e s s s s D s N s K s s s s K sF s = = = − = + + + + = = = + + + + = = − − = =− + = = 所以,原函数为 f t e t t ( ) 1 2 sin −2 = + (4)因为 ( 1) ( ) ( ) ( ) ( ) 2 2 2 2 D s s s j s j s s s F s = + − = + = 令 D(s) = 0 , 有 p = − j 1 和 p = j 2 分别为二重根, 且 1 p 和 2 p 为共轭复根,故设 s j K s j K s j K s j K F s − + + + − + + = 12 22 2 21 2 11 ( ) ( ) ( ) 则各系数为 0 [( ) ( )] 0 4 1 4 1 4 1 4 1 ( ) [( ) ( )] 22 1 2 12 2 21 11 2 2 1 2 11 1 1 1 = = + = = = = − = = − = + = =− − − = =− K s j F s ds d K K K e e j j e s j s K s j F s s j j j s p s 所以,原函数为 f t j te j te t t jt jt sin 2 1 4 1 4 1 ( ) = − = − 14-4 图(a) ,(b), (c) 所示电路原已达到稳态,t=0 时把开关 S 合上,分别画出运算电路
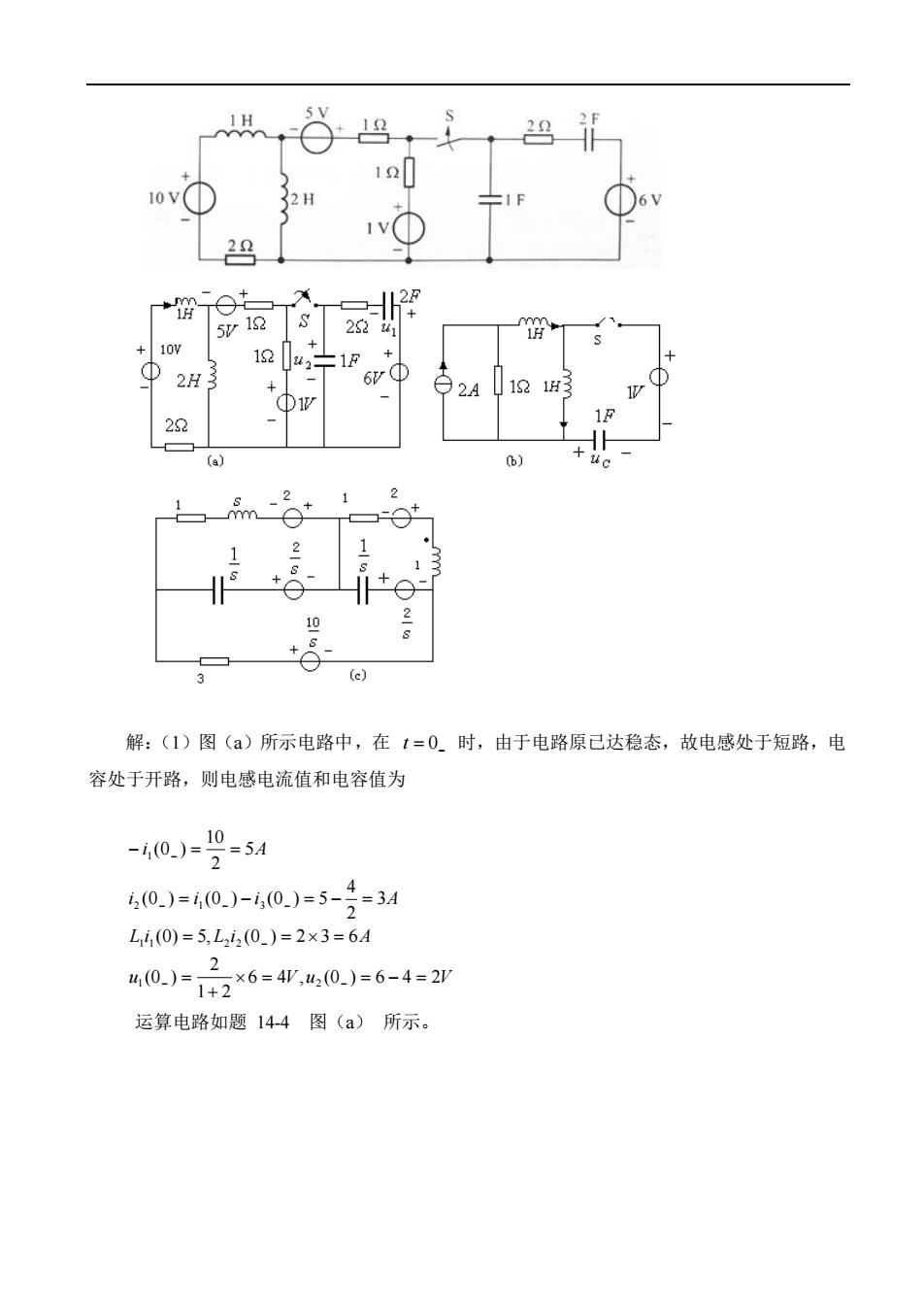
12 )6 1v① 2 12u 2H 6- 92A121H 1 22 1 10 (e) 解:(1)图()所示电路中,在t=0时,由于电路原已达稳态,故电感处于短路,电 容处于开路,则电感电流值和电容值为 40.)=40.)-40.)=5-1=31 L44(0)=5,L4(0.)=2×3=6A %0.1-26=40)=6-4=2r 运算电路如题14-4图(a)所示
解:(1)图(a)所示电路中,在 = 0− t 时,由于电路原已达稳态,故电感处于短路,电 容处于开路,则电感电流值和电容值为 u V u V L i L i A i i i A i A 6 4 , (0 ) 6 4 2 1 2 2 (0 ) (0) 5, (0 ) 2 3 6 3 2 4 (0 ) (0 ) (0 ) 5 5 2 10 (0 ) 1 2 1 1 2 2 2 1 3 1 = = − = + = = = = = − = − = − = = − − − − − − − 运算电路如题 14-4 图(a) 所示