第3章电阻电路的一般分析 3-1 在一下两种情况下,画出图示电路的图,并说明其节点数和支路数(1)每个元件作为一条支路处理: (2)电压源(独立或受控)和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理。 (a) 6) 题31图 解:(1)每个元件作为一条支路处理时,图(a)和(b)所示电路的图分别为题解3-1图 (al)和(bl)。 图(al)中节点数n=6,支路数b=11 图(61)中节点数n=7,支路数b=12 (2)电压源和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理时,图() 和图(b)所示电路的图分别为题解图(a2)和(62)。 图(a2)中节点数n=4,支路数b=8 图(b2)中节点数n=15,支路数b=9 (a1) 0b1 (a2) 题解1-3图
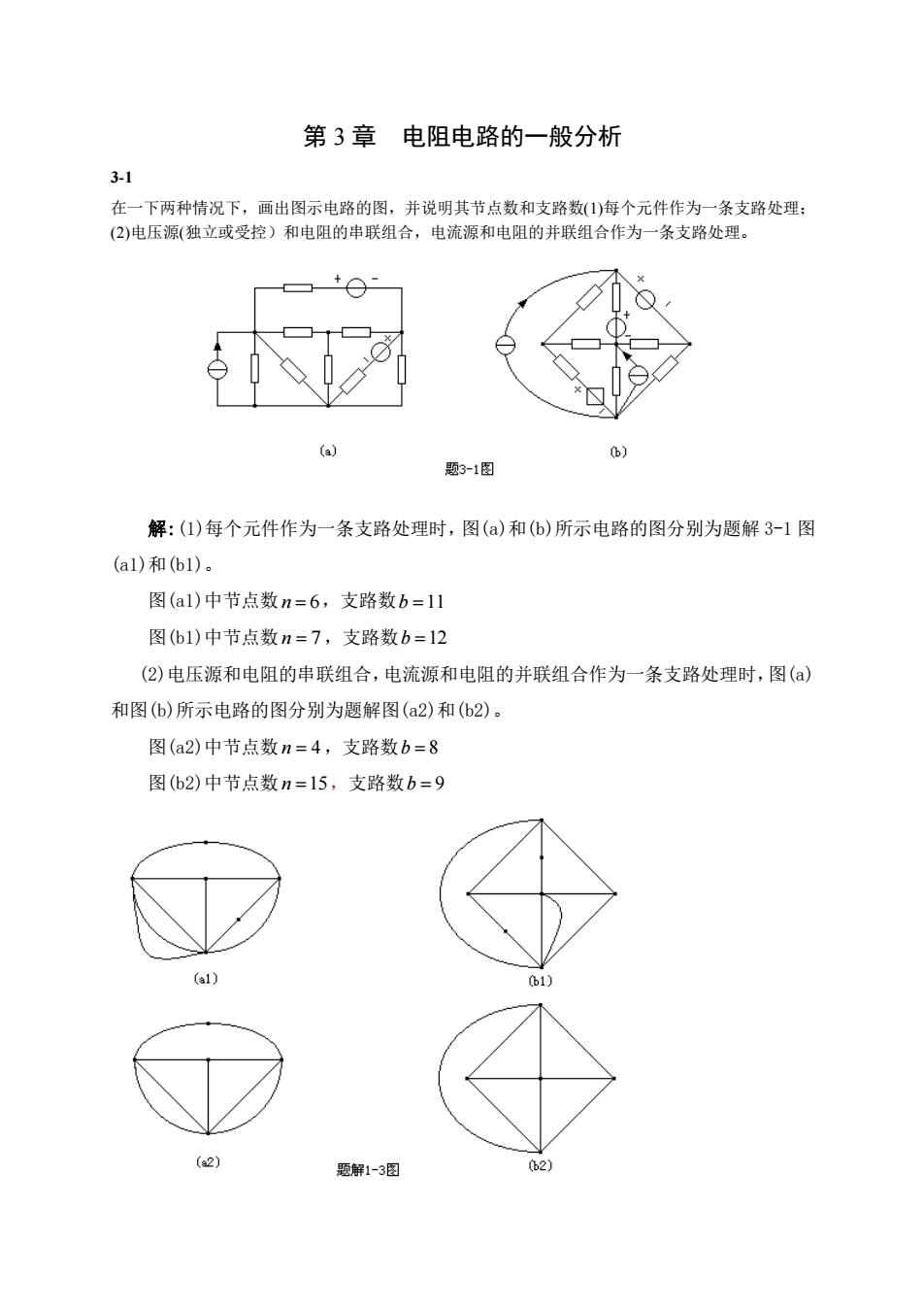
第 3 章 电阻电路的一般分析 3-1 在一下两种情况下,画出图示电路的图,并说明其节点数和支路数(1)每个元件作为一条支路处理; (2)电压源(独立或受控)和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理。 解:(1)每个元件作为一条支路处理时,图(a)和(b)所示电路的图分别为题解 3-1 图 (a1)和(b1)。 图(a1)中节点数 n = 6 ,支路数 b =11 图(b1)中节点数 n = 7 ,支路数 b =12 (2)电压源和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理时,图(a) 和图(b)所示电路的图分别为题解图(a2)和(b2)。 图(a2)中节点数 n = 4 ,支路数 b = 8 图(b2)中节点数 n =15,支路数 b = 9
3-2 指出题3-1中两种情况下,KCL,KL独立方程数各为多少? 解:题3-1中的图(a)电路,在两种情况下,独立的KCL方程数分别为 (1)n-1=6-1=5(2)n-1=4-1=3 独立的KVL方程数分别为 (1)b-n+1=11-6+1=6(2)b-n+1=8-4+1=5 图(b)电路在两种情况下,独立的KCL方程数为 (1)n-1=7-1=6(2)n-1=5-1=4 独立的KVL方程数分别为 (1)b-n+1=12-7+1=6(2)b-n+1=9-5+1=5 对题图()和(b)所示G,各画出4个不同的树,树支数各为多少? 3 题3-3图 解:一个连通图G的树T是这样定义的:(山)T包含G的全部结点和部分支路:(2)T本身是 连通的且又不包含回路。根据定义,画出图(a)和(b)所示图G的4个树如题解33图a)和(b)所示。树 支数为结点数减一。故图()的数有树支,图b)的树有树支 n-1=6-1=5o
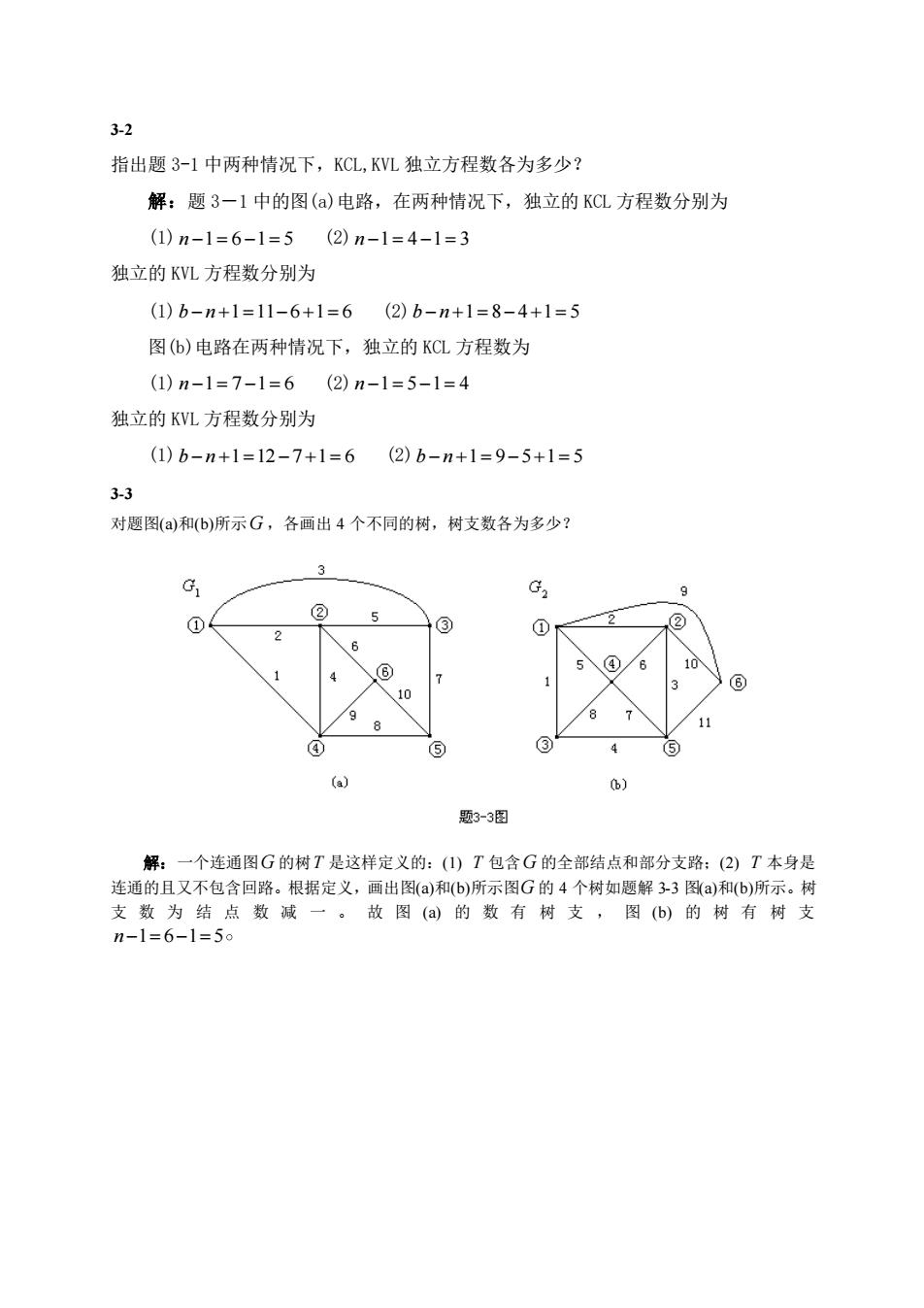
3-2 指出题 3-1 中两种情况下,KCL,KVL 独立方程数各为多少? 解:题 3-1 中的图(a)电路,在两种情况下,独立的 KCL 方程数分别为 (1) n −1= 6 −1= 5 (2) n −1= 4 −1= 3 独立的 KVL 方程数分别为 (1) b − n +1=11−6+1= 6 (2) b − n +1= 8− 4+1= 5 图(b)电路在两种情况下,独立的 KCL 方程数为 (1) n −1= 7 −1= 6 (2) n −1= 5−1= 4 独立的 KVL 方程数分别为 (1) b − n +1=12−7 +1= 6 (2) b − n +1= 9−5+1= 5 3-3 对题图(a)和(b)所示 G ,各画出 4 个不同的树,树支数各为多少? 解:一个连通图 G 的树 T 是这样定义的:(1) T 包含 G 的全部结点和部分支路;(2) T 本身是 连通的且又不包含回路。根据定义,画出图(a)和(b)所示图 G 的 4 个树如题解 3-3 图(a)和(b)所示。树 支 数 为 结 点 数 减 一 。 故 图 (a) 的 数 有 树 支 , 图 (b) 的 树 有 树 支 n− = − = 1 6 1 5
①2② 5① ③ ①2②5③ ④8 ④ ① ① 10 5④/6 5 ④ 3 /11 4⑤ ③4⑤ 题解3-3图 34 图示桥形电路共可画出16个不同的树,试一一列出(由于节点树为4,故树支为3,可 按支路号递减的方法列出所有可能的组合,如123,124,.,126,134,135,.等, 从中选出树)。 3-4图 解:图示电路,16个不同的树的支路组合为: (123),(124),(125),(136),(145), (146),(156),(234),(235),(236),(246) (256),(345),(346),(456) 35 对题图3-3所示的G,和G,任选一树并确认其基本回路组,同时指出独立回路数和网 孔数各为多少?
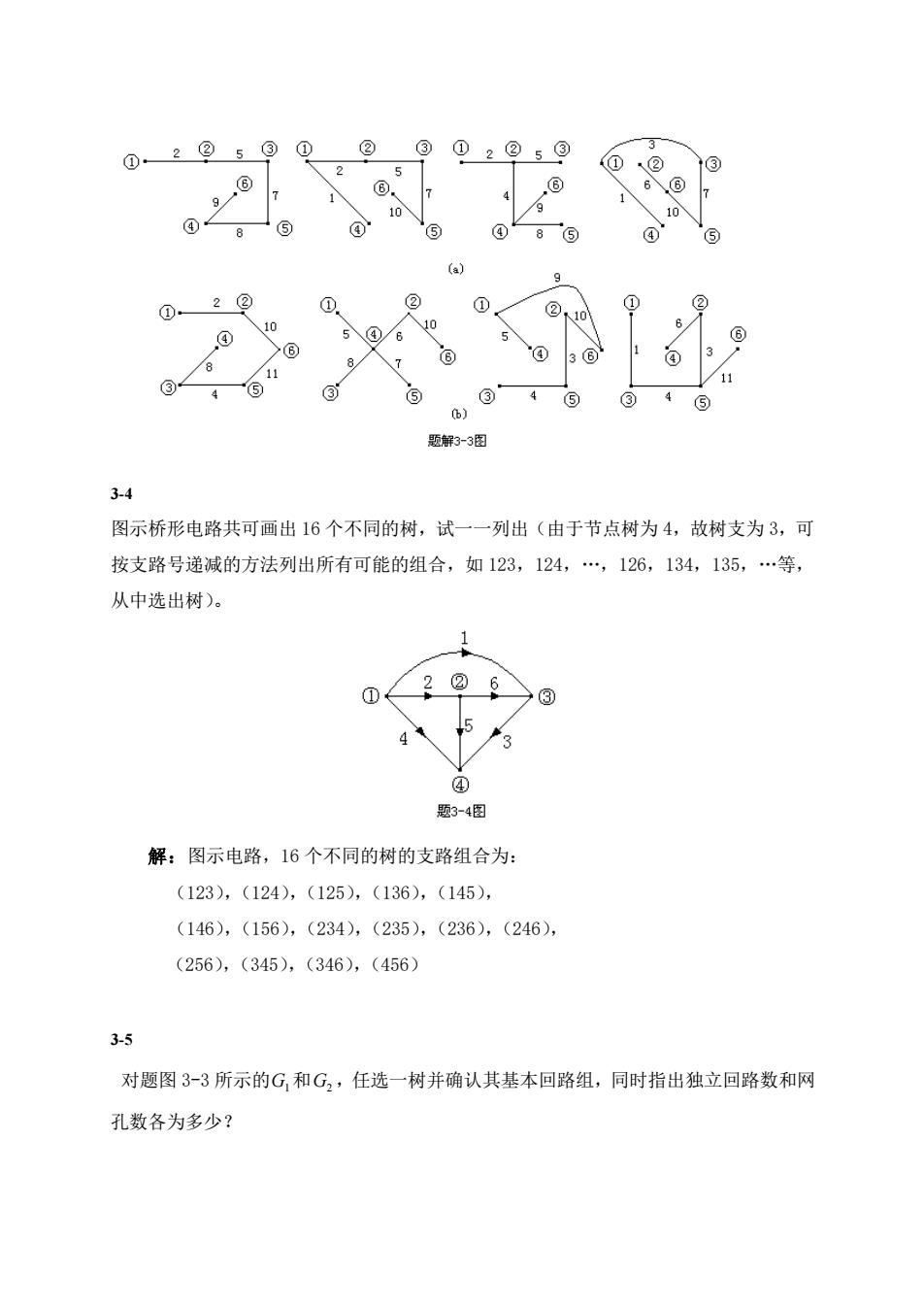
3-4 图示桥形电路共可画出 16 个不同的树,试一一列出(由于节点树为 4,故树支为 3,可 按支路号递减的方法列出所有可能的组合,如 123,124,.,126,134,135,.等, 从中选出树)。 解:图示电路,16 个不同的树的支路组合为: (123),(124),(125),(136),(145), (146),(156),(234),(235),(236),(246), (256),(345),(346),(456) 3-5 对题图 3-3 所示的 G1 和 G2 ,任选一树并确认其基本回路组,同时指出独立回路数和网 孔数各为多少?

器品o 路,是, 6,7,10,ii 题解3-5日 0) 解:在连通图G中,由树支和一个连支组成的回路称为G的基本回路(或单连支回 路),基本回路是独立回路,网孔也是独立回路,因此,基本回路数=独立回路数十网 孔数。对一个节点数为n,支路数为b的连通网,其独立回路数1-(b-n+)。从题图 3-3所示的G,和G,中任选一树,(见题解3-5图(a)和(b)中粗线所示),对应于这一树 的基本回路分别为1=5,1,=6。 3-6 对图示非平面图,设:(1)选择支路(1,2,3,4)为树:(2)选择支路(5,6,7, 8)为树,问独立回路各有多少?求其基本回路组。 解:图中有结点数n=5,支路数b=10,故独立回路树为b-n+1=10-5+1=6 (1)选择支路(1,2,3,4)为树,对应的基本回路组为:(1,2,3,4,5),(1, 2,3,7)(1,2,6),(2,3,4,8),(2,3,9),(3,4,10) (2)选择支路(5,6,7,8)为树,对应的基本回路组为:(1,5,8),(2,5,6, 8),(3,6,7),(4,5,7),(5,7,8,9),(5,6,10)
解:在连通图 G 中,由树支和一个连支组成的回路称为 G 的基本回路(或单连支回 路),基本回路是独立回路,网孔也是独立回路,因此,基本回路数=独立回路数+网 孔数。对一个节点数为 n ,支路数为 b 的连通网,其独立回路数 l = (b − n +1) 。从题图 3-3 所示的 G1 和 G2 中任选一树,(见题解 3-5 图(a)和(b)中粗线所示),对应于这一树 的基本回路分别为 l 1 = 5,l 2 = 6。 3-6 对图示非平面图,设:(1)选择支路(1,2,3,4)为树;(2)选择支路(5,6,7, 8)为树,问独立回路各有多少?求其基本回路组。 解:图中有结点数 n = 5 ,支路数 b =10 ,故独立回路树为 b − n +1=10−5+1= 6 (1)选择支路(1,2,3,4)为树,对应的基本回路组为:(1,2,3,4,5),(1, 2,3,7),(1,2,6),(2,3,4,8),(2,3,9),(3,4,10) (2)选择支路(5,6,7,8)为树,对应的基本回路组为:(1,5,8),(2,5,6, 8),(3,6,7),(4,5,7),(5,7,8,9),(5,6,10)

3-7 图示电路中R=R=102,R,=42,R=R=82,R=22,4=20,46=40,用支 路电流法求解电流:。 R61 ①u 题3-7图 解:本题电路有4个节点,6条支路,独立回路数为6一4+1=3。设各支路电流和 独立回路绕行方向如图所示,由KCL列方程,设流出节点的电流取正号。 节点①1+12+6=0 节点② -42+1+14=0 节点③ -i4+i3-i6=0 由KVL列方程 回路1 2i。-814-102=-40 回路Ⅱ -101,+1012+43=-20 回路Ⅲ-41,+81,+81,=20 联立求解以上方程组,得电流5=0.956A 注:由本题的求解过程可以归纳出用支路电流法分析电路的步骤如下: (1)选定各支路电流的参考方向: (2)任取(-1)个结点,依KCL列独立结点电流方程: (3)选定(b+1)个独立回路(平面回路可选网孔),指定回路的绕行方向,根据KL列 写独立回路电压方程:
3-7 图示电路中 R1 = R2 =10 ,R3 = 4 ,R4 = R5 = 8 ,R6 = 2 ,us3 = 20V,us6 = 40V ,用支 路电流法求解电流 5 i 。 解:本题电路有 4 个节点,6 条支路,独立回路数为 6-4+1=3。设各支路电流和 独立回路绕行方向如图所示,由 KCL 列方程,设流出节点的电流取正号。 节点① i 1 + i 2 + i 6 = 0 节点② − i 2 + i 3 + i 4 = 0 节点③ − i 4 + i 5 − i 6 = 0 由 KVL 列方程 回路Ⅰ 2i 6 −8i 4 −10i 2 = −40 回路Ⅱ −10i 1 +10i 2 + 4i 3 = −20 回路Ⅲ − 4i 3 + 8i 4 + 8i 5 = 20 联立求解以上方程组,得电流 i 5 = −0.956 A 注:由本题的求解过程可以归纳出用支路电流法分析电路的步骤如下: (1)选定各支路电流的参考方向; (2)任取(n-1)个结点,依 KCL 列独立结点电流方程; (3)选定(b-n+1)个独立回路(平面回路可选网孔),指定回路的绕行方向,根据 KVL 列 写独立回路电压方程;