
第12章三相电路 12-1 己知对称三相电路的星形负载阻抗Z=(165+84)2,端线阻抗乙=(2+川2,中线阻抗, 中线阻抗乙w=1+)2,线电压U,=380P。求负载端的电流和线电压,并作电路的相量图 A o 交名食名 c。色。2 a B (C) 题解12-1图 解:按题意可画出对称三相电路如题解12-1图()所示。由于是对称三相电路,可以 归结为一相(A相)电路的计算。如图(6)所示。 220∠0° 1,z+2167+8511744-26.98A 根据对称性可以写出 iB=a2i4=1.174∠-146.98°A ic=aig=1.174∠93.02A 负载端的相电压为 0w=2Zi.=(165+j85)×1.174∠-26.98°=217.90∠0.275
第 12 章 三相电路 12-1 已知对称三相电路的星形负载阻抗 Z = (165 + j84) ,端线阻抗 Z1 = (2 + j1) ,中线阻抗, 中线阻抗 ZN = (1+ j1) ,线电压 U1 = 380V 。求负载端的电流和线电压,并作电路的相量图。 题解 12-1 图 解:按题意可画出对称三相电路如题解 12-1 图(a)所示。由于是对称三相电路,可以 归结为一相(A 相)电路的计算。如图(b)所示。 令 V U U A 0 220 0 3 1 = = ,根据图(b)电路有 1.174 26.98 A 167 85 220 0 1 = − + = + = Z Z j U I A A 根据对称性可以写出 1.174 146.98 A 2 I B = a I A = − 1.174 93.02 A I C = aI B = 负载端的相电压为 U AN = ZI A = (165 + j85)1.174 − 26.98 = 217.900.275
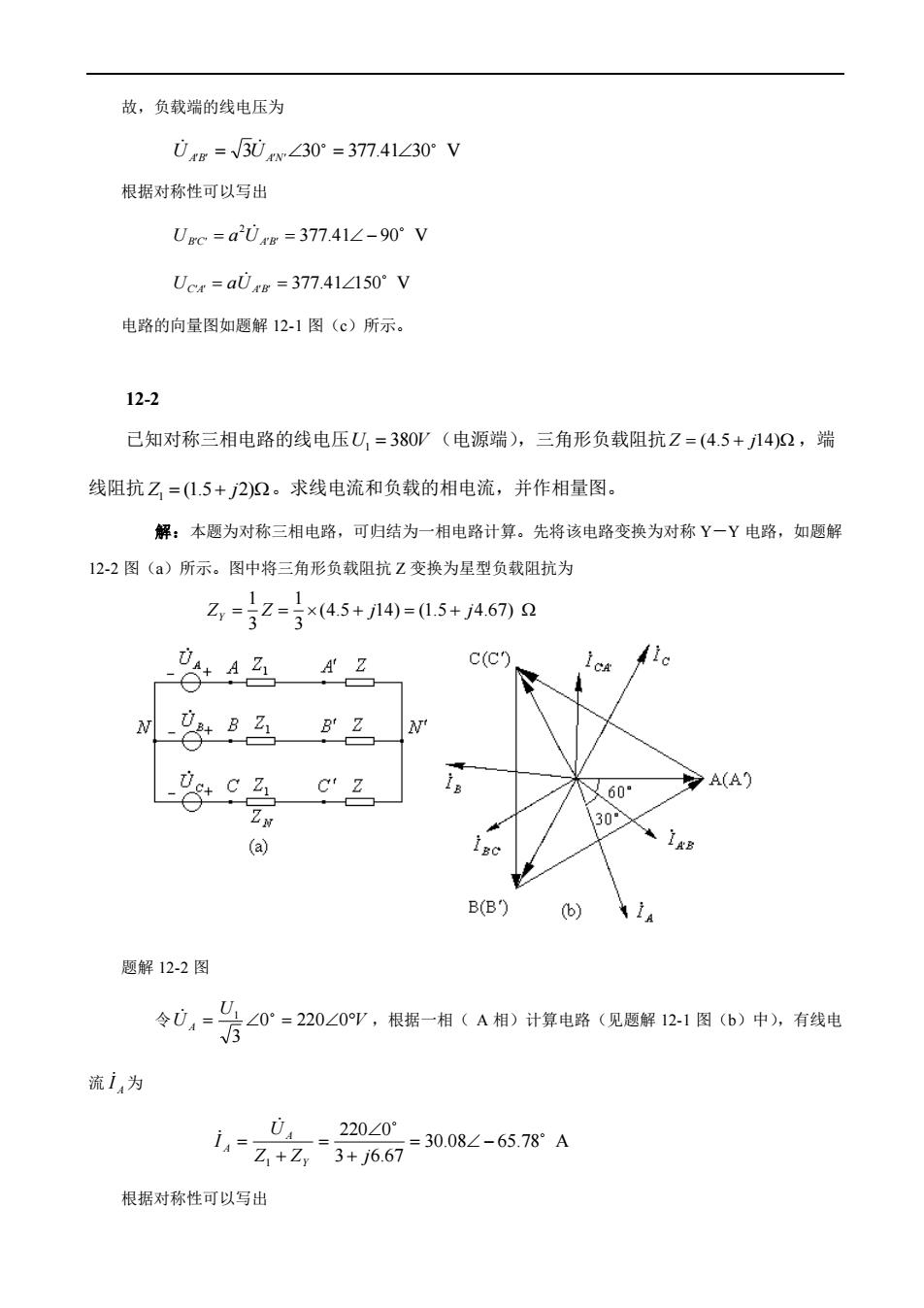
故,负载端的线电压为 0rs=V30∠30°=377.41∠30°V 根据对称性可以写出 Uc=a20rs=377.41∠-90°V Ucr=a0xr=377.41∠150°V 电路的向量图如愿解12-1图(©)所示。 12-2 已知对称三相电路的线电压U=380(电源端),三角形负载阻抗Z=(4.5+14)2,端 线阻抗乙=(1.5+2)2。求线电流和负载的相电流,并作相量图。 解:本题为对称三相电路,可归结为一相电路计算。先将该电路变换为对称Y一Y电路,如愿解 12-2图(a)所示。图中将三角形负载阻抗Z变换为星型负载阻抗为 乙-7-写45+n40=05+46初n 4是 A'Z c(c + C'Z A(A 60· Zx 30 (a) B(B) (b) 题解12-2图 0三发∠0=220∠0V,根据一相(A相)计算电路(见题解21图(b)中,有线 流i为 1,=Z+z3#667=0084-6578A 220∠0° 根据对称性可以写出
故,负载端的线电压为 3 30 377.41 30 V U AB = U AN = 根据对称性可以写出 377.41 90 V 2 UBC = a U AB = − 377.41 150 V UCA = aU AB = 电路的向量图如题解 12-1 图(c)所示。 12-2 已知对称三相电路的线电压 U1 = 380V (电源端),三角形负载阻抗 Z = (4.5 + j14) ,端 线阻抗 Z1 = (1.5+ j2) 。求线电流和负载的相电流,并作相量图。 解:本题为对称三相电路,可归结为一相电路计算。先将该电路变换为对称 Y-Y 电路,如题解 12-2 图(a)所示。图中将三角形负载阻抗 Z 变换为星型负载阻抗为 = = (4.5 + 14) = (1.5 + 4.67) 3 1 3 1 Z Z j j Y 题解 12-2 图 令 V U U A = 0 = 2200 3 1 ,根据一相( A 相)计算电路(见题解 12-1 图(b)中),有线电 流 A I 为 30.08 65.78 A 3 6.67 220 0 1 = − + = + = Z Z j U I Y A A 根据对称性可以写出

in=a2i4=30.08∠-185.78A ic=ad,-30.08∠54.22°A 利用三角形连接的线电流与相电流之间的关系,可求得原三角形负载中的相电流,有 1w=方30=7372-3578A 而 igc=a2irg-17.37∠-155.78°A icx=alrg=17.37∠84.22°A 电路的相量图如题解12-2图(b)所示。 注:从12-1和12-2题的计算分析中可以归纳出Y一Y联结的对称三相正弦交流电路的如下特点: (1)中性点等电位,有U 八=0,中线不起作用,即不管有无中线,电路的情况都一样。 (2)各相具有独立性。即各相的电压和电流只与各相的电源和负载有关,且和各相电源为同相序 的对称量。 由以上特点可以得出计算对称三相电路的一般方法和步骤为: (①)应用△-Y等效变挨(乙,=。,心,-∠-30)把三相电路化为对称的Y-Y联 3 接。 (2)用虚设的、阻抗为零的中线联接中性点,取出一相(一般为A相)电路,计算对应的电压、 电流。 (3)根据对称性,推出其余二相的电压、电流。 需要注意,对称三相电路中电压和电流相值与线值之间的关系,即(1)Y联接中, U,=V30∠30°,i=ih:(2)△联接中,U=Ut,i=V5i4-30°。 12-3 将题12一2中负载Z改为三角形连接(无中线)。比较两种连接方式中负载所吸收的复功率 12-4 图示对称工频三相耦合电路接于对称三相电源,线电压U,=380,R=302,L=0.29H M=0.12H。求相电流和负载吸收的总功率
30.08 185.78 A 2 I B = a I A = − 30.08 54.22 A I C = aI A = 利用三角形连接的线电流与相电流之间的关系,可求得原三角形负载中的相电流,有 30 17.37 35.78 A 3 1 I AB = I A = − 而 17.37 155.78 A 2 I BC = a I AB = − 17.37 84.22 A I CA = aI AB = 电路的相量图如题解 12-2 图(b)所示。 注:从 12-1 和 12-2 题的计算分析中可以归纳出 Y—Y 联结的对称三相正弦交流电路的如下特点: (1)中性点等电位,有 0 ' . = NN U ,中线不起作用,即不管有无中线,电路的情况都一样。 (2)各相具有独立性。即各相的电压和电流只与各相的电源和负载有关,且和各相电源为同相序 的对称量。 由以上特点可以得出计算对称三相电路的一般方法和步骤为: (1)应用△-Y 等效变换( ZY Z△ 3 1 = , 30 3 = − AB A U U )把三相电路化为对称的 Y-Y 联 接。 (2)用虚设的、阻抗为零的中线联接中性点,取出一相(一般为A相)电路,计算对应的电压、 电流。 (3)根据对称性,推出其余二相的电压、电流。 需要注意,对称三相电路中电压和电流相值与线值之间的关系,即(1)Y 联接中, U1 = 3U ph30 , ph I I = 1 ;(2)△联接中, U Uph = 1 , I1 = 3I ph− 30 。 12-3 将题 12—2 中负载 Z 改为三角形连接(无中线)。比较两种连接方式中负载所吸收的复功率。 12-4 图示对称工频三相耦合电路接于对称三相电源,线电压 U1 = 380V ,R = 30,L = 0.29H , M = 0.12H 。求相电流和负载吸收的总功率

R 题12-4图 解:电路为对称三相电路,去耦等效电路如题解124图所示,可归结为一相(A相)电路来计算。 U=(R+joL-joM)i 令相电压0,为心,-号40=2020,则相电流,为 220/0° 1,R+t-m30+938=3593c-6064 根据对称性可以写出 i。=a2i=3.593∠-180.66°A ic=ad=3.593∠59.34°A 负载吸收的总功率为 P=312R=3×3.5932×30=1161.78W R L-M B。昌5 c。-M m 题解124图 12-5 题12-5图所示对称Y-Y三相电路中,电压表的读数为1143.16V,Z=(15+j153)2, 乙,=0+j2)2。求:(1)图中电流表的读数及线电压UB:(2)三相负载吸收的功率:(3)如果A相的
题 12-4 图 解:电路为对称三相电路,去耦等效电路如题解 12-4 图所示,可归结为一相(A 相)电路来计算。 A A U R j L j M I = ( + − ) 令相电压 U A 为: V U U A = 0 = 2200 3 1 ,则相电流 A I 为 A R j L M j U I A A = − + = + − = 3.593 60.66 30 53.38 220 0 ( ) 根据对称性可以写出 3.593 180.66 A 2 I B = a I A = − 3.593 59.34 A I C = aI A = 负载吸收的总功率为 P = 3I A 2R = 33.5932 30 =1161.78 W 题解 12-4 图 12-5 题 12-5 图所示对称 Y—Y 三相电路中,电压表的读数为 1143.16V, Z = (15 + j15 3), Zl = (1+ j2) 。求:(1)图中电流表的读数及线电压 UAB ;(2)三相负载吸收的功率;(3)如果 A 相的

负载阻抗等于零(其他不变),再求(1)(2):(4)如果A相负载开路,再求(1)(2)。(5)如果加接零 阻抗中性线Z、=0,则(3)、(4)将发生怎样的变化? A。O马A名 ⊙ A Z B 0 题12-5图 解:图示电路为对称Y一Y三相电路,故有0xw=0,可以归结为一相(A相)电路的计 算。 根据题意知Urg=1143.16,则负载端处的相电压U为 Uw-g-"格6-60v 而线电流为 1=贤-602A(电流表谈数) Z30 故电源端线电压U为 U=U,=V3Z+Zh,=V5×32.232×22=12282V (1)令0w=220∠0V,,则线电流i.为 220/0° Z 故图中电流表的读数为6.14 (2)三相负载吸收的功率为 P=3R=3×6.12×30=3349W (3)如果A相的负载阻抗等于零(即A相短路),则B相和C相负载所施加的电压均为电源线 电压,即N”点和A点等电位,而
负载阻抗等于零(其他不变),再求(1)(2);(4)如果 A 相负载开路,再求(1)(2)。(5)如果加接零 阻抗中性线 Z N = 0 ,则(3)、(4)将发生怎样的变化? A A B C N Z Z Z Zl Zl Zl V A' B' C' 题 12-5 图 解:图示电路为对称 Y-Y 三相电路,故有 UNN = 0 ,可以归结为一相(A 相)电路的计 算。 根据题意知 UAB =1143.16V ,则负载端处的相电压 U AN 为 660 V 3 1143.16 3 = = = A B A N U U 而线电流为 22 A 30 660 1 = = = Z U I A N (电流表读数) 故电源端线电压 UAB 为 UAB =U1 = 3 Z1 + Z I1 = 3 32.232 22 =1228.2 V (1)令 UAN V = 2200 ,则线电流 A I 为 6.1 33.69 A 30 20 220 0 = − + = = Z j U I AN A 故图中电流表的读数为 6.1A。 (2)三相负载吸收的功率为 P = 3I A 2R = 36.1 2 30 = 3349 W (3)如果 A 相的负载阻抗等于零(即 A 相短路),则 B 相和 C 相负载所施加的电压均为电源线 电压,即 N 点和 A 点等电位,而