
20第2章模拟PLL的传递函数 2.3.32类PLL举例 2.2节中曾对重要的二阶2类PLL做了大量的描述。本节将要考察2类环路的一 些更进一步的变化结构。应当注意,对于所有2类或更高类的PLL,K心=∞,因而就 不必考虑1类环路所固有的环路带宽和DC增益之间的权衡。 1,仅有积分器的环路滤波器 假设环路滤波器的传递函数很简单,为F(s)=K2/s;并且这个公式中的比例通路 的增益K,=0。于是,环路的各个传递函数为 C=K,Ho)=本K0=7+底kK 52 (2-37) 2 式(2-37)有两个突出特点: (1)H(s)的分子中没有零点。(试与式(2-15)相比,传递函数(2-15)适用于常见的 二阶2类PLL。) (2)分母中的极点位于虚轴上的s=土j√KK。K2处。 前面的H(s)中没有分子零点,想必不会有增益峰值,但式(237)中极点的配置导致 极点频率处的无限大增益。没有零点使2类PL处于稳定性的边界上。任何一个微小 的扰动都会产生极点频率上的无阻尼正弦振荡。环路中附加任何一个微小的相位滞后, 就会引起完全的不稳定,表现为幅度以指数增长的振荡。由此,下面这个经验请晰可见: 2类反馈环路的环路滤波器在它的传递函数中必须至少包含一个零点,才能实现 24」稳定的闭环运行。更一般地说,一个n类环路(n>1)的滤波器传递函数必须包含至少 (n一1)个零,点,否则环路将不稳定。 2.三阶2类PL 二阶2类PLL是在PLL文献中大量遇见的简单结构,但在实际中却并非如此。 大多数实用的PLL还会增加一些高频极点。其中有些极点也许是故意加入的,以获得 系统频率响应中更陡峭的滚降率,或者为了抑制由检相器产生的高频扰动。关于需要 增加滤波的实例将在后面几章中给出。其他的极点是由分布参数引起的,是无法避免 地由反馈环路中的实际元件的频率响应的限制而产生的:其中包括杂散电容、放大器 带宽的限制和VCO控制通路中的低通电路。 在许多情况下,极点的频率远高于所需的环路带宽,因而这些高频极点(至少在初 步设计分析阶段)可以被忽略。在其他情况下,从一开始就必须考虑某些或所有的高 频极点。本节讨论最简单的情况,即只增加一个有用的极点,这在实际应用中是非常 重要的一步。 ☐传递函数 只增加一个极点的开环传递函数可表示为 o0=Kn-(1+品)o (2-38) =(1+)1+6

2.3其他环路阶数和类型 21 其中的第三个极点位于s=一1/x3、K=KK。x2/和b=t2/x3。由于这是一个三阶 PLL,所以有三个参数:K、x2和b。经过一些处理后,闭环传递函数变为 Kx2(sx2+1) H(s)=+Kst+Kta (2-39) s(x2/b十1) E(s)Ksi+Kta 口归一化 通过归一化可以把其中一个参数隐藏起来,因而简化了传递函数的表达式。我喜 欢对2做归一化,虽然也可以选择对其他参数做归一化。由此,我们定义无量纲的归 一化增益和归一化频率如下 K'=Kt:,p=st2 (2-40) 25 因而,归一化的闭环传递函数变为 K'(p+1) Hp)=D76+P+Kp+R (2-41) 2(/b+1) E(p)=Db十P+Rp+K 评注:试考察一个二阶2类PLL,其乘积Kx2=4。这个关系式不能沿用到三阶 环路,在三阶环路中存在三个极点,使阻尼系数的概念无论怎样都会变得模糊不清。 阻尼系数的另外可能的含义将在下面探讨。 ☐频率响应 把复变量p的直角坐标分量定义为p=u十jv=oπ2十jwr2。对于任意指定的K'和b 的值,我们可以容易地对v的某个取值范围求出H(Gjo)|或|E(Gj)|,如图2-9中的举例 那样,其中的频率比例尺是归一化为/K'=ω/K。但是,K'和b的一些具体取值只给 出一些孤立的曲线;而一个完整的曲线族将会有用得多。但频率响应不能表示为 图2-4至图2-7那样的、以归一化后剩下的两个独立参数为参量的二维曲线族。我们 应当把曲线族画成一个三维图,或者画成几个二维曲线族的图。每个二维图只对应其 中一个参数的某个值(比如K'),而另一个参数(比如b)则对应图中的各条曲线。但这 两种方法都不能给我们满意的图示。在高阶环路的情况下,问题变得更无法控制。在 第3章中我们将用图示法来应对。 ☐大K时的近似 K的一般取值范围在1至10之间,但偶尔需要大得多的值,可以从50至100,甚 至更大。虽然这样大的值并不多见,但考察一下关于大K的近似系统传递函数是很有 启发性的。为此,我们考虑低频区传递函数的近似表达式(即|p很小时),并用H(p) 表示,因此,分母中的三次项可以略去;此外,还有一个高频的近似表达式(即|p很大 时),并用HH()表示,因此,分子分母中的零次项可以略去。作为再一个约束,b也不 可以很小。于是,两个传递函数变为 H(p)-K'(2+1) K +RD+K,Hmp)-p6+D+R (2-42)
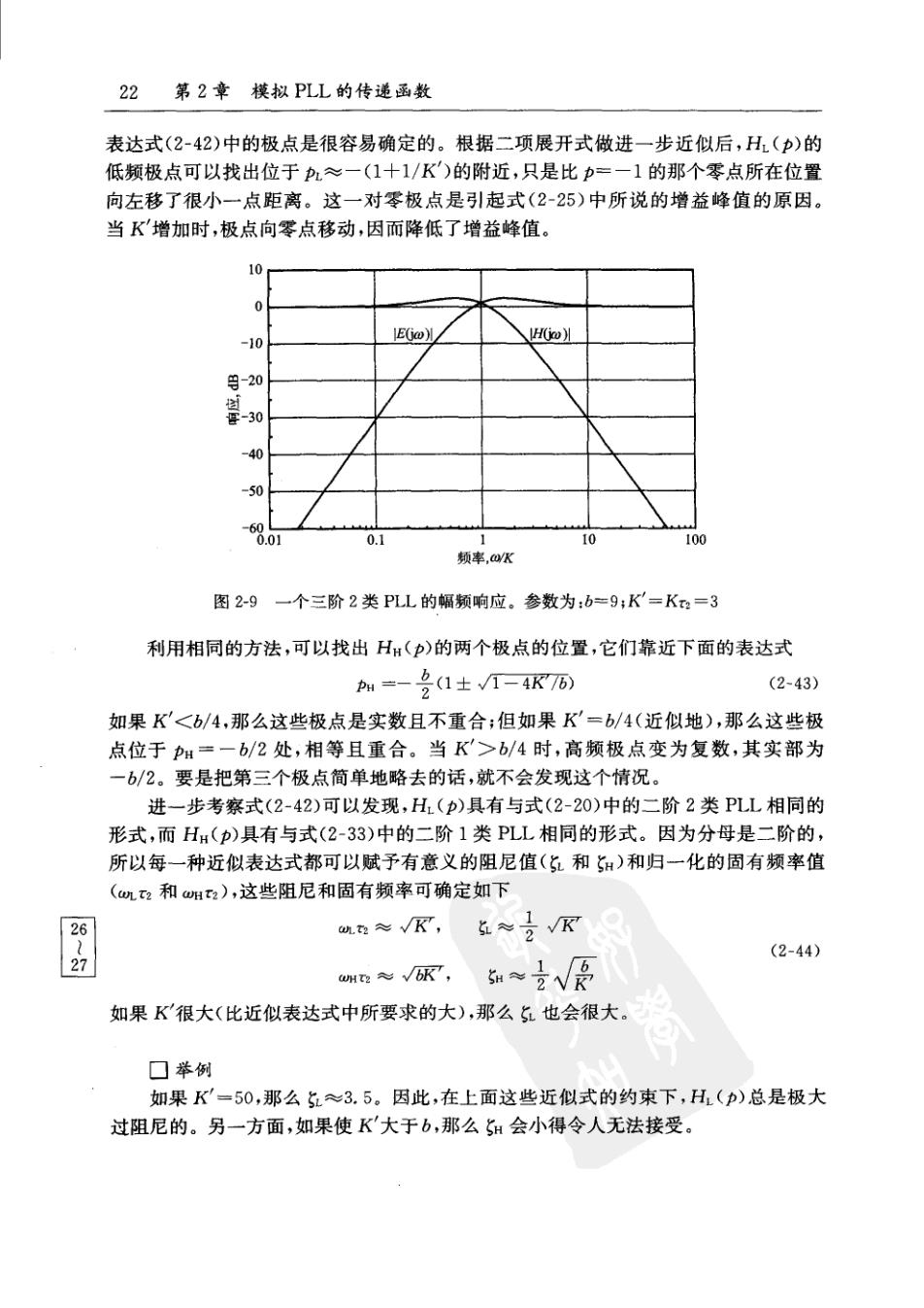
22 第2章模拟PLL的传递函数 表达式(2-42)中的极点是很容易确定的。根据二项展开式做进一步近似后,H(p)的 低频极点可以找出位于p≈一(1十1/K')的附近,只是比p=一1的那个零点所在位置 向左移了很小一点距离。这一对零极点是引起式(2-25)中所说的增益峰值的原因。 当K'增加时,极点向零点移动,因而降低了增益峰值。 10 0 -10 E) H() 号-20 每-30 -40 -50 -60 0.01 10 100 频率,aK 图2-9一个三阶2类PLL的幅频响应。参数为:b=9;K=Kx2=3 利用相同的方法,可以找出H:(p)的两个极点的位置,它们靠近下面的表达式 m=-名(1士V-4K76) (2-43) 如果K'<b/4,那么这些极点是实数且不重合;但如果K'=b/4(近似地),那么这些极 点位于p:=一b/2处,相等且重合。当K>b/4时,高频极点变为复数,其实部为 一b/2。要是把第三个极点简单地略去的话,就不会发现这个情况。 进一步考察式(2-42)可以发现,H()具有与式(2-20)中的二阶2类PLL相同的 形式,而HH(p)具有与式(2-33)中的二阶1类PLL相同的形式。因为分母是二阶的, 所以每一种近似表达式都可以赋予有意义的阻尼值(5和5H)和归一化的固有频率值 (wt2和wt2),这些阻尼和固有频率可确定如下 ≈√K, 点≈是K 2品 (2-44) wH2≈√, 如果K很大(比近似表达式中所要求的大),那么也会很大。 口举例 如果K'=50,那么5≈3.5。因此,在上面这些近似式的约束下,H(p)总是极大 过阻尼的。另一方面,如果使K'大于b,那么5H会小得令人无法接受

参考文献 23 ☐稳定性边界 如果把x3=x2(即b=1)代人式(2-38),那么第三个开环极点就与起稳定作用的那 个零点互相抵消,结果的传递函数与式(2-37)中的那些传递函数完全一样,而式 (2-37)中环路滤波器只是一个简单的积分器。因此,b=1是一个稳定性边界:如果b< 1,则环路不稳定。另一方面,式(2-43)中给出的那些近似的高频极点表明,一个三阶2 类PLL,只要b>1,则无论K'多大都是稳定的。当然,如果K'太大,阻尼就将小得令人 无法接受。 2.3.4.更高类的PLL 5.1.1节解释了为什么有时需要一个3类PIL。一个三阶3类PLL的传递函数 可以表示为 G)=长(1++) H(s)= K(+袋+) (2-45) +K(++ E(s)= +K(3++) 我们需要3个独立参量来确定这个PLL的特性,所以它的特性不像二阶环路那样 容易掌握。其中的有些特性将在第3章中做进一步探讨。 4类或更高类型的锁相环是极少使用的,本书不做介绍。 参考文献 2.1 D.H.Wolaver,Phase-Locked Loop Circuit Design,Prentice Hall,Englewood Cliffs, NJ.1991. 28 是 海

第3章图示法 基于传递函数的频率响应曲线族只是为了理解PLL特性而使用的图示法中的一 种形式。多年来,人们想出了另外一些传递函数的图示方法,包括根轨迹图3山、伯德 图3刀、奈奎斯特图3和尼科尔斯图3.幻。这些是非常完善的方法,在大量的控制系统 的书籍中都有详尽的描述;这里所引用的参考文献是每种方法的早期初创者的书籍与 文章。 其中的两种方法在PLL分析中被广泛使用:根轨迹图和伯德图。奈奎斯特图和尼 科尔斯图使用了与伯德图相同的数据,但做出的曲线却不一样。虽然根轨迹图和伯德 图在PLL的分析中占有主导地位,但PLL工程师们也可得益于尼科尔斯图。下文将 说明如何把根轨迹图和伯德图使用于几个实用PLL的传递函数中,接着再简单说一下 奈奎斯特图,然后再说一下尼科尔斯图。3.5节将指出,闭环频率响应曲线可以很容易 地用生成伯德图或尼科尔斯图的同一开环数据画出来。 本章中的全部内容都适用于模拟(即连续时间和连续幅度的)PLL。而且,由于所 有的4种图示技术都是为了对传递函数进行图示,并且传递函数仅适用于线性电路, 29所以这些方法中没有一个是可以用于非线性PLL的。 3.1根轨迹图 从闭环响应的极点[即1十G(s)的根]的位置中,我们可以获得对锁相环特性的深 人理解。极点的位置随着环路增益(或其他参数)的改变而改变。这些极点在、平面上 移动而画出的路线就叫做根轨迹。根轨迹图的特点(比如路径的条数、与坐标轴的交 点等)可以使用一些简单的规则(见附录3A),从已知开环极点和零点的位置确定。 3.1.1根轨迹图的描述 一条轨迹通常是对应于增益的某个范围(从近似于零到非常大的值)而画出的。 轨迹是从开环极点处(增益为零)开始的,结束于开环的零点(增益无穷大),有的零点 可以位于无穷远处。任何一个PLL的开环传递函数都可写为G(s)=K。K:F(s)/s。 因此,至少总有一个极点位于s=0处,这不包括F(s)中的任何积分器的极点。开环零 点是F(s)的零点