
3.1根轨迹图 25 绘制根轨迹图可以使用下面几种方法。 (1)很简单的传递函数(比如,一阶和二阶PLL)的根轨迹可以通过观察来画出。 其轨迹是一些简单的几何图形,这将在下面说明。图3-1和图3-2中示出了一些例子。 (2)轨迹的复数分支与s平面上实轴与虚轴的交点可以用附录3A中的方法来确定。 J@ sx-1/2 r=1/4 图3-1一个二阶1类PLL的根轨 图3-2一个二阶1类PLL的根轨迹 迹图,其中的滞后滤波器为 图,其中的滞后超前滤波器为 F(s)=1/(sx+1) F(s)=(s2十1)/(sm+1) (3)特征方程的根的位置是在其他参数固定在某些值之后、让增益K在某个范围 内变化时计算出来的,然后把这些位置画到图上。一条轨迹就是对应一组固定参数值 条件下,改变K(一般都是改变K)而得到的全部这样位置的集合。图3-3和图3-4是 这样的两个实例,其中的根是用数值法并求助于计算器算出的,图是手工描的。图3-6 图3-3一个三阶2类PLL的根轨迹图,其中的零点在sx2=一1,第3个极点在5π=一b
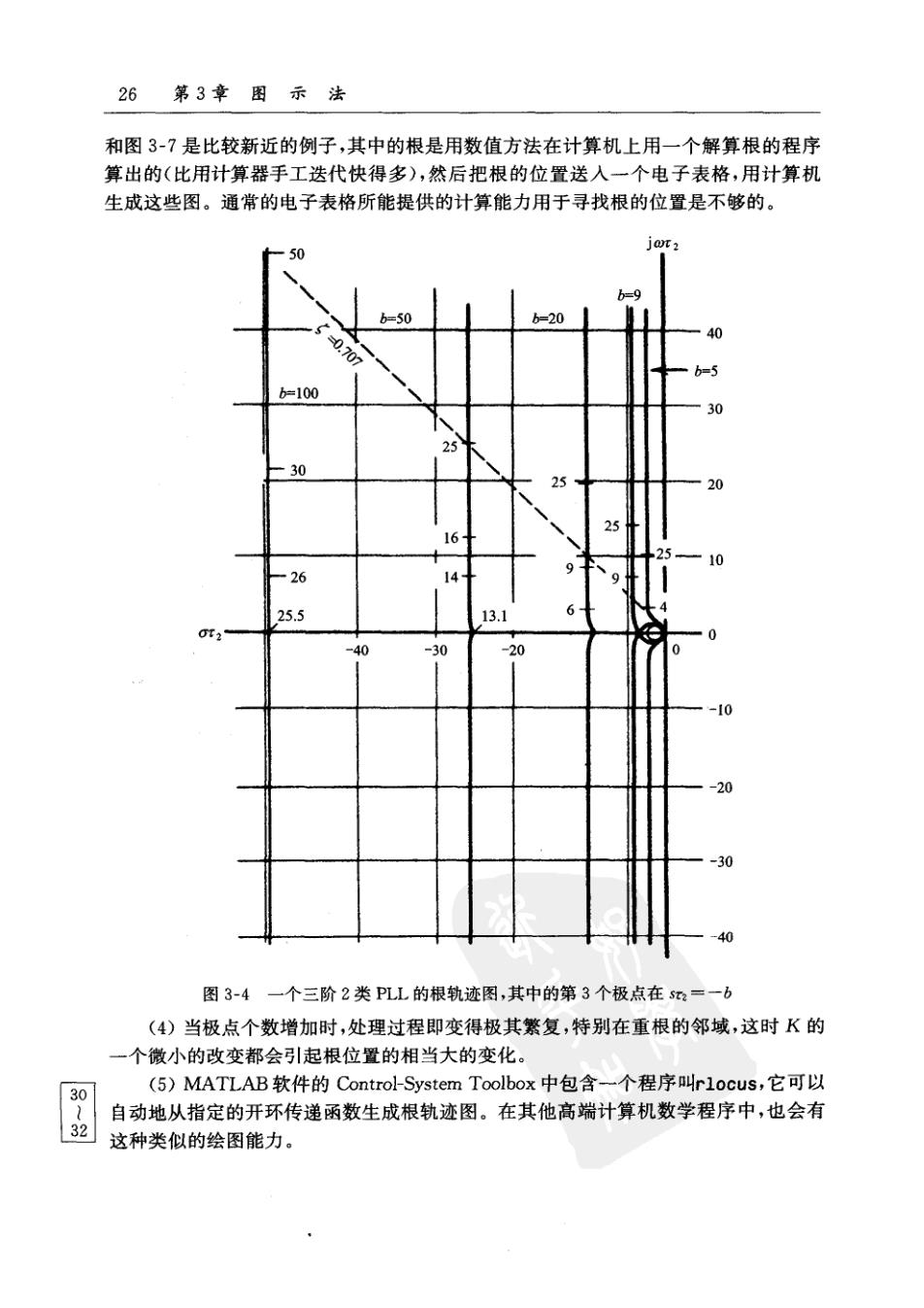
26第3章图示法 和图3-7是比较新近的例子,其中的根是用数值方法在计算机上用一个解算根的程序 算出的(比用计算器手工迭代快得多),然后把根的位置送人一个电子表格,用计算机 生成这些图。通常的电子表格所能提供的计算能力用于寻找根的位置是不够的。 jor2 50 b=9 b=50 b=20 -0.707 b=5 b=100 30 25 30 25 20 25 16 10 26 14 25.5 131 0r2 -40 -30 -20 -10 -20 -30 -40 图3-4一个三阶2类PLL的根轨迹图,其中的第3个极点在s2=一b (4)当极点个数增加时,处理过程即变得极其繁复,特别在重根的邻域,这时K的 一个微小的改变都会引起根位置的相当大的变化。 (5)MATLAB软件的Control-System Toolbox中包含一个程序叫rlocus,它可以 30 自动地从指定的开环传递函数生成根轨迹图。在其他高端计算机数学程序中,也会有 32 这种类似的绘图能力

3.1根轨迹图 27 3.1.2稳定性判据 如果所有的极点都位于5平面的左半平面内,那么反馈环路是稳定的;如果其中任 意一个极点位于右半平面,那么反馈环路是不稳定的。、平面的虚轴是稳定与不稳定 之间的分界线;任何一个闭环极点都不可以在虚轴上。而且,作为良好的工作习惯,甚 至不允许任何一个极点靠近虚轴,因为这样会导致很差的稳定性容限、阻尼不足以及 过大的增益峰值。 3.1.31类PLL的根轨迹 这里将展示一些1类PIL的根轨迹图,以说明最简单的曲线实例以及如何进行初 期设计。 1.一阶环路 也许都能想到,一阶环路[F(s)=1]的根轨迹是最简单的。它有一个位于原点的 单一开环极点和一个位于无穷远处的单一零点。闭环极点随着增益的增加而沿着负 实轴从零移动到无穷大。 2.带滞后滤波器的环路 只有一个滞后滤波器F(s)=1/(sx+1)的环路有两个开环极点,一个在零点,另一 个在s=一1/x处,它的两个零点在无穷远处。根轨迹图如图3-1所示。当增益从零开 始增加时,两个极点在负实轴上相向移动。当这两个极点在Kπ=1/4处相遇时,即变 成一对共轭复数,并随着增益的进一步增加而沿着。=一1/(2x)的垂直直线移动到无 穷远处。当增益很大时,阻尼变得非常差。 3.带有滞后超前滤波器的环路 滞后超前滤波器的传递函数为F(s)=(sx2十1)/(sx1+1)。从超前项得到的好处 可以从图3-2中看出。这些极点起先沿着负实轴相向移动,而在相遇之后变为复数。 因为滤波器的零点是有限值的,所以根轨迹的复数部分现在变成了一个以一1/x2为圆 心的圆,而不是图3-1中那条垂直的直线。对于适度偏小的增益,阻尼是很小的,但超 过一个最小增益之后,阻尼则随着增益的增加而增加。当增益足够大时,轨迹最后回 到实轴,环路进入过阻尼状态。轨迹中的一条分支终结于那个有限值的零点;另一条 分支结束于负实轴的无穷远处。 3.1.42类PLL的根轨迹 2类PLL在实际应用中占有主导地位。 1.二阶环路 图3-2中所示的是一个二阶1类环路的根轨迹曲线。如果环路滤波器真的具有一 个完美的积分器,那么开环的两个极点都会位于5=0处,因而根轨迹的圆形部分就会33 从s=0开始,圆心会在s=一1/x2,圆的半径就会是1/x2。除了这些不同外,图形与

28第3章图示法 图3-2所示基本一致。 2.三阶环路 三阶2类PLL的根轨迹图以不同的比例尺绘制在图3-3和图3-4中。当b取大值 时(第三个极点远远超过以2归一化的零点的位置,该零点位于p=sx2=一1),图3-3 表示出的靠得很近的根轨迹(即,当K'=K2的值相对很小的情况下)几乎与二阶2类 PLL的相同。但在图3-4中,当K变得足够大时,第三个极点的影响被强烈地显现出 来:那个向外移动的极点(从=0出发的极点中的一个)和向内移动的第三个极点相 遇,变成一对复极点,并趋于p=一(b一1)/2的垂直渐近线。这个行为证实了2.3.3节 中关于“高增益”的分析,在那个分析中发现垂直渐近线大约位于p=一b/2处。实际 上,对于b的一切值,我们都发现垂直渐近线位于=一(b一1),而不仅仅是对于b的 大值。 而且,如果b很小,那么第三个极点具有主要的影响力,甚至小增益时也是这样。 事实上,如果b<9,则对于所有的增益值,两个从p=0出发的极点将永远是复数而不 返回实轴。当b取小值时,就要求不能忽略第三个极点而必须给予明确的考虑。b≈9 的条件对实际设计有好处。会出现这样的情况,即要求带宽尽量的大(大的K'值)以及 由第三个极点给出尽量多的滤波(大的3值),并保持良好的阻尼。b=9和K=3的 这个条件使所有三个闭环极点重合于p=一3。b的较小值会削弱阻尼,而b的较大值 又给不出那么多的滤波。从某个角度来看,参量选择为b=9和K′=3(或它的邻域), 在有些要求下差不多是最佳的。 注意:对这些参数取值的实际容差常常达不到要求的精度,因而无法实现这种准 优化的参数选择。 如果<1,那么从p=0出发的两个极点从不同路径进人右半平面,因而对一切 K>0,环路都是不稳定的。 3.1.53类PLL的根轨迹 三阶3类PLL的所有三个开环极点都位于s=0。为了便于图示,我们假设2个零 点重合于s=一1/x2。图3-5画出了这种情况下的根轨迹。该图的一般性特征对于任 何一个3类环路都是相当典型的,所以应当认为是有用的。图中有一个不常见的特 点:轨迹在增益取小值时进入了右半平面;环路在小增益下是不稳定的。较大的增益 把极点带入左半平面,因而使工作稳定。这个环路被称作是条件稳定的。这个行为是 与前面的1类和2类环路完全相反的,那些环路是无条件稳定的。所以当使用3类环 路时,必须防止因增益下降而进入不稳定区。 评注:(1)几个3类PLL的设计者已经发现重合的零点是有用的。这一选择被 Tausworthe.)以及Tausworthe和Crow[3..)推荐为最佳选择。(2)无数的文献极为详 细地论述了1类和2类PLL的特性;第1章中的参考文献列出了许多这样的文章。与 L34 之相反,关于3类PLL的文献却寥寥无几。除了参考文献[3.5]和参考文献[3.6]之

3.1根轨迹图 29 外,Meyr和Ascheid所著的书[a,门中提供了分析方法、设计指南和性能曲线。第5章和 第8章中还引用了其他几个参考文献,其中讲到了有理由使用3类PLL的情况。 jaω 2个零点 3个极点 609 Fs)-+1y 6T)2 图3-5一个三阶3类PLL的根轨迹图,其中的2个零点重合于52=一1。 与虚轴的交点出现在K=是,与实轴的交点出现在K- 4 3.1.6高阶PLL的根轨迹 我们假定PLL的阶数超过了三阶,那么对根轨迹图会有什么影响呢?如果开环的 所有极点和零点都已确定,就可以不费多大力气计算并画出一条单一的根轨迹。但当 需要对不同参数值画出一整套根轨迹曲线族的时候,工作量就大大增加了。试考虑其 中一个比较简单但又相当常见的高阶的实例:一个四阶2类PLL,它的新增加的极点 位于s=一1/3和s=一1/x4。与前面一样,我们做关于2的归一化,并取K=Kr2作 为独立变量,这样仍然还有两个参数b=2/x和b4=2/x,需要考虑。一套完整的根 轨迹曲线图再也不能像图3-3和图3-4那样画在一张或两张图上了,而是需要一大批 图纸才能画出合理覆盖b、b4全部空间的曲线图。要是极点再多的话,情况会更糟。 如果一个四阶2类PLL极点被规定为使≥x4,那么当4=3时,第四个极点将 具有最长的时间常数和最大的影响力;这个极端情况下的曲线图,即3=τ4=2/b,被 示于图3-6和图3-7中,其中b有几个取值。为了简洁,图中并没有画出下半平面内的 35 共轭复极点,也没有画出全部实极点的位置。 两个开环极点从p=0出发,另外两个从p=一b出发。在后两个极点中,一个沿 着负实轴向左移至无穷大,另一个向右移至p=一1处的开环零点。从p=0出发的那 两个开环极点,随着K从零增加,最初以一对共轭复极点移动。对于所有的K'>0,如 果(8一4√3)≈1.0718<b<(8+4√3)≈14.928,那么这两个极点将永远为复极点。如 果b=(8+4v3),则当K'=4(1+2/W3)/3≈2.8729时,三个极点在p=一2(1+1/W3) ≈一3.15470处相遇。但对于b的上述取值,K'取任何其他值时,有两个极点将是复