
2.2二阶PLL15 这样做几乎没有什么用。我们可以从图2-4至图2-7中确定3dB的带宽,但这样确定 的带宽并没有什么确切的含义。二阶2类PLL的低通响应|H(jw)的3dB带宽可以 用下式计算: w-k(分+好+V1+京+京) (2-24) 该带宽在5取值较大时接近于K,这在图2-6中可以清楚地看出。 4.增益峰值 图2-4至图2-7中的响应曲线呈现明显的峰值,尤其在小阻尼时。|E(jw)|的高通 响应仅当5<√O.5≈0.707时才有峰值,当:大于此值时不出现峰值。低通响应 |H(j)川在小阻尼时呈现很大的峰值,但对于二阶2类PLL,无论阻尼取多大,这种峰 值都不会完全消失。 为什么低通曲线总是有峰值呢?在小阻尼(5<0.707)的情况下,传递函数的复 数极点靠近s平面的虚轴,因此小阻尼时的谐振效应变得很明显。但对于较大阻尼的 情况,峰值依然存在,甚至在过阻尼(>1)的情况下,也有峰值:也就是说,那些仅有实 极点的环路没有谐振效应。在大阻尼情况下出现峰值的原因是H(s)分子中的那个位 于s=一1/x2处的零点。这个零点使|H(Gw)川随频率的增加而增加;这种增加最后被那 些极点的滚降所阻止。随着K的增加(阻尼的增加),零点与最近的一个极点之间的距 离就减小,但只要K取任何有限的值,这个极点永远不会与零点重合。因此,二阶2类 18 PLL的|H(Gjw)|总表现出一定的增益蜂值。 如果零点使增益出现峰值,那为何不去除这个零点以消除峰值呢?2.3.3节将说 明,这样的零点是保证2类PLL稳定工作所必需的。更广义地说,为了使一个n类的 环路工作稳定,就需要有(一1)个零点。有些工程师认为三阶的环路可以抑制峰值; 但一直缺乏明确的证据。对于图2-1中的这种PLL结构,增益峰值是为了从环路滤波 器的积分器上获得好处而必须付出的代价。 适度的峰值在许多应用中是无关大局的,但并非对所有的应用都如此。试设想这 样一种情况:有许多PLL级联在一起,比如在电信系统巾的一个转发器链路中。如果 每个转发器仅有1dB的峰值(相当于≈1,一般认为是一个不小的阻尼),如果转发器 链路中共有100个转发器(并非太夸张的数目),又假定没有采取任何预防性措施,那 么这个转发器链路将会有100dB的峰值,那就是一场灾难。电信设备中转发器的常用 的标准规定最大峰值仅为0.1dB。 从式(2-20)传递函数H(s)的分析中可以看出,一个二阶2类PLL的增益峰值可 以用下式来计算 8x4 增益蜂值=1010g (2-25) 8x4-452-1+√8g+1 峰值与阻尼之间的关系曲线见图2-8。小于0.1dB的峰值要求>4.4
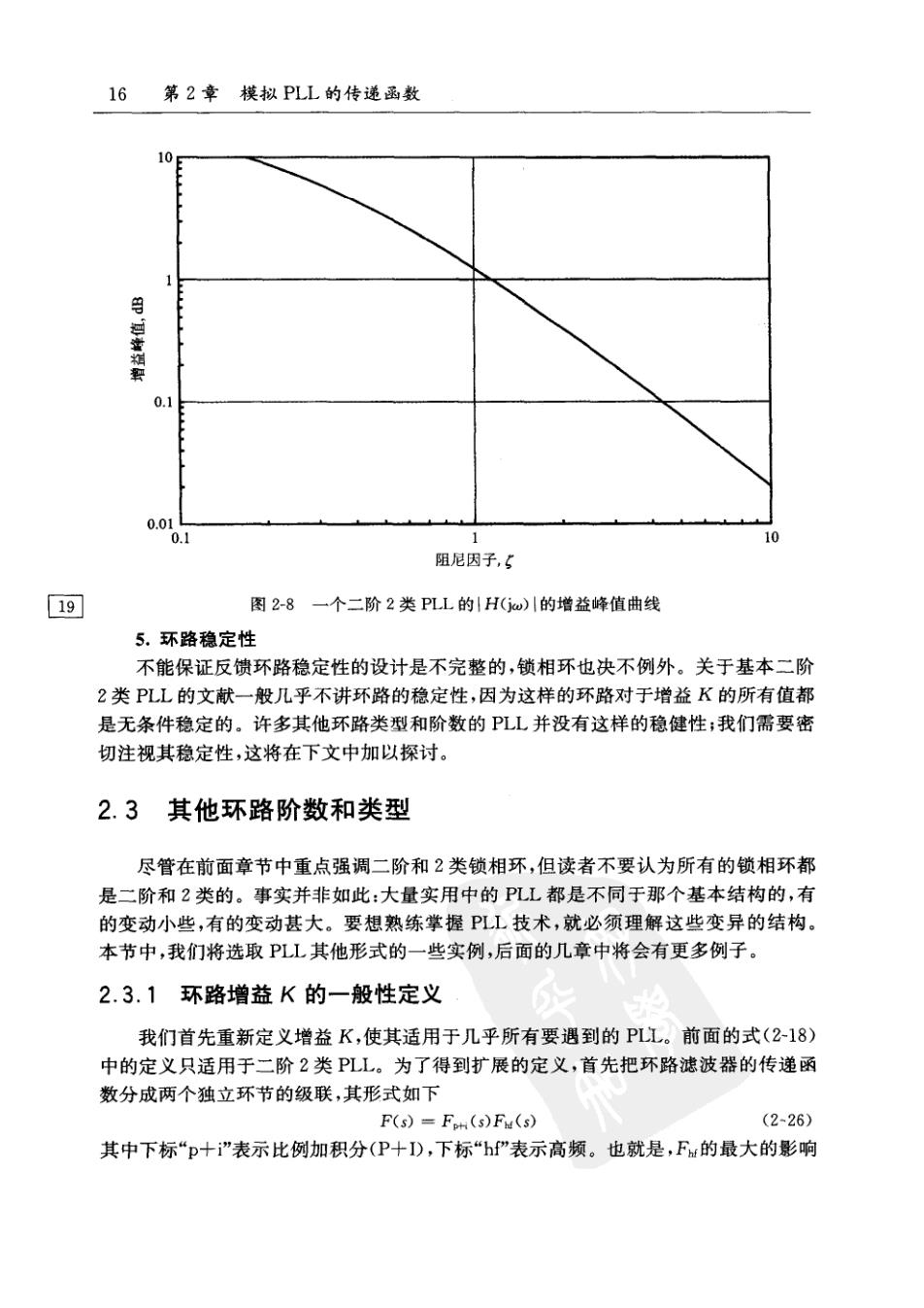
16 第2章模拟PLL的传递函数 10 0.1 0.0 0.1 1 10 阻尼因子,5 19 图2-8一个二阶2类PLL的|H(jw)|的增益峰值曲线 5.环路稳定性 不能保证反馈环路稳定性的设计是不完整的,锁相环也决不例外。关于基本二阶 2类PLL的文献一般几乎不讲环路的稳定性,因为这样的环路对于增益K的所有值都 是无条件稳定的。许多其他环路类型和阶数的PLL并没有这样的稳健性;我们需要密 切注视其稳定性,这将在下文中加以探讨。 2.3其他环路阶数和类型 尽管在前面章节中重点强调二阶和2类锁相环,但读者不要认为所有的锁相环都 是二阶和2类的。事实并非如此:大量实用中的PLL都是不同于那个基本结构的,有 的变动小些,有的变动甚大。要想熟练掌握PLL技术,就必须理解这些变异的结构。 本节中,我们将选取PLL其他形式的一些实例,后面的几章中将会有更多例子。 2.3.1环路增益K的一般性定义 我们首先重新定义增益K,使其适用于几乎所有要遇到的PLL。前面的式(2-18) 中的定义只适用于二阶2类PLL。为了得到扩展的定义,首先把环路滤波器的传递函 数分成两个独立环节的级联,其形式如下 F(s)=Fn(s)Fu(s) (2-26) 其中下标“p十i”表示比例加积分(P十I),下标“hf”表示高频。也就是,F的最大的影响

2.3其他环路阶数和类型 17 是在“高”频区,而在一般情况下,这个“高”频响应的大部分位于PLL的带宽之外。对 Fu(s)唯一的约束是Fu(O)必须有界且非零。 在这个一般性的公式中,“P十”因子可以有任意多个积分器,不像2类PLL中只 有一个。“P+”的表达式可以写为 F()=K1+K+十… 2 (2-27) 其中K:具有(时间)”的量纲,从而保证和式中的每一项都是无量纲的。比较常见 的情况是采用的积分器的个数不大于1,但有时用两个积分器很合适(见2.3.4节)。 使用两个以上的积分器则是极少见的。 评注:经常遇到这样的情况:所用的积分器是不完美的,即不是用一个积分器,而 是用一个截止频率很低的低通滤波器取而代之。在这种情况下,一个方便的办法是, 在F+(s)中(不是在Fu(s)中)需要的地方用1/(s十s:)来代替积分器,因而把一个低通 滤波器充当一个积分器使用。这个方法对于模拟电路是极其必要的,因为在模拟电路 中几乎不可能实现完美积分器。在实际工作中,不完美积分器可以做得充分接近于理 20 想的1/5,因而使这样的近似可以被接受。在2.3.2节中可以见到这样的一个例子。 依据式(25),使用更一般性的环路滤波器的开环传递函数变为 G=KKEE@=KK(K+++…)Fa(s) -KKK50(1+急++…号 =(1++老+…)8 (2-28) 由此,得到K的一般性定义为 K=KK。K1Fu(O) (2-29) 当然,这个定义也适用于二阶2类PLL,其中当>2时,K:=0,Fu(s)=1。 评注:虽然式(2-28)好像规定了P十I环节的具体结构,但几乎所有实用的环路滤 波器都可以写成这种形式,无论其电路是如何配置的。附录3B中有几个例子。 可以看出,K是完全由比例通路确定的:积分器和高频效应对该定义丝毫没有影 响。然而,K对于PLL的响应速度和带宽具有决定性的影响,这个影响将在后文中经 常提到。从这个特点得出了下面的经验: 环路滤波器中的任何滤波操作,对于环路带宽和速度一般只起到次要的影响。对 环路起主要影响的是环路增益K。 增益穿越频率 我们把增益穿越频率awe定义为使|G(jw)|=l(即0dB)时的频率,并以rad/s为 单位。如果表达式(2-28)中的所有系数都是已知的,那么w的确切表达式可以从式 (2-28)中提取出来,但下面这个简单的近似表达式可以提供更多的信息。如果 K2/K1w《1(在2类PLL中aw>1/x2),并且如果|Fu(jw)l/IFt(0)≈1,那么 您≈K (2-30)

18第2章模拟PLL的传递函数 因而,在条件不严格的情况下,开环增益穿越OdB的频率点在Krad/s的附近。 那么,上面这样的近似究竟有多好?我们来考虑一个二阶2类PLL,它在s=jK处 21]的开环增益可以很容易找出,为G(jK)2=1+1/(2)。下面是一些选取的数值: 20log|G(jK)(dB) 0.5 3.0 0.707 0.97 1.0 0.26 气 0.017 5 0.0004 对于这个例子,在小阻尼时的近似是很差的,而在中等或大阻尼时是很好或极好 的。对于其他类型和阶数的PLL,可以期望有类似的结果。 评注:(1)对于任何一种PLL,环路增益K都是最重要的参数,在全书中也是这样 被使用的。(2)对K的重要性的强调(或认识)在PLL的文献中并没有被广泛接受;其 他许多作者选择了a,这个选择令人非常不满意。但也有一个突出的例外,Wolaver在 他所写的书2门中使用了K,这与本书是一样的。(3)在阅读其他文献时必须要注意; 符号K经常被用来表示增益因子,但与式(2-29)中定义的K是不一样的。K的其他 含义并非有错,而只是不同而已;希望阅读时注意。(4)有些作者错误地把“环路增益” 用B来表示,也就是表示为一个无量纲的量。无论怎样定义,PLL的环路增益都总是 以频率为量纲的;一个无量纲的定义是毫无意义的。 2.3.21类PLL举例 1类PLL在环路中只有一个积分器,位于VCO中。可以举出其中几个有用的 电路。 1.一阶PLL 最简单的PLL是完全没有环路滤波器的。这种PLL可以用2.3.1节中的公式描 述,其中F+(s)=K1,Fu(s)=1。它的增益和传递函数如下: K=KK.K =Kpc (2-31) 和 ()KH(E()R (2-32) 所以环路增益K(对于这个例子,等于3B带宽)是设计者唯一可用的参数。如果DC 增益必须很大(一般为了保证良好跟踪而要求的,见5.1.1节),那么带宽也必须很大。 22因此,在一阶环路的情况下,如果要有很好的跟踪能力,则窄带与此不相配;由于这个 原因,窄带的一阶环路不常用。然而,一阶环路经常出现在文献中,主要是因为这些环 路分析起来最容易,而且还因为从一阶环路中选出的行为往往可以近似地推广到比较 复杂的、因而比较难于分析的PLL

2.3其他环路阶数和类型 19 2.带滞后滤波器的二阶PLL 一种稍微复杂一些的PLL包含了一个环路滤波器,而且F+(s)=K1,F(s)= 1/(sx+1)。这个结构具有与简单的一阶PLL相同的环路增益K和DC增益Kc,但它 的系统函数和误差传递函数是二阶的: K/t H(9=2+5+K=子+20s+a (2-33) s(s+1/x) s(s十2w) E(s)=++K7.=2+23+ 上式中的参数定义为 =2 = (2-34) 现在只有两个系数K和x,所以不能独立地确定w、5和Kc这3个参数。如果DC增 益必须很大、必须很小,那就要求x必须很大,其结果是环路过分欠阻尼 注意:和5的这些定义与二阶2类PLL中的定义大不相同。 虽然这是一个严格意义上的二阶PLL,但最好被看作一阶的PLL,而它所增加的 滤波只是为了抑制系统响应中的高频成分而已。其实,|H(jw)|是以一12dB/倍频为 渐近线的,而不像二阶2类PLL那样以一6dB/倍频为渐近线。而且,由于H(s)的分 子中没有零点,所以只要>0.707,就不会出现增益峰值。把这些性质组合起来构成 的这种PLL,在不要求窄带的应用中是很有用的。现在有大量的这类PLL使用于通信 转发器中。 3.带有滞后超前滤波器的二阶PLL 从锁相环的早期(即20世纪50年代)开始,人们就认识到了对窄带和大D℃增益 的同时要求,但在那个时候还没有很好的D℃放大器,所以也就没有满意的积分器。取 而代之的是,在早期的文献中和许多PLL中使用了无源的滞后超前滤波器,其传递函 数为 o-密-(+0)》 (2-35) 其中x2<。上式也可以解释为是一个比例加不完美积分器的滤波器,并且K,= x2/m,K2/K,=1/x2一1/x。环路增益可定义为K=KK。K1,DC增益是Kc=KK。, 23 而环路传递函数为 s+1/x1 K(s+1/r2) H()=子+5(K+1/a)+K/ (2-36) s(s+1/) E()=2+s(K+1/)+K/ 这里,我们可以完全自由地、独立地确定DC增益、环路带宽和阻尼:与之相比,前面的 1类PLL的例子却没有这样的自由。这种自由解释了为什么在早期的二阶PLL中普 遍使用滞后超前滤波器的原因