中国地质大学（武汉）：《信号与系统 Signals and Systems》课程教学资源（课件讲稿）第二章 LTI连续时间系统的时域分析

第二章LT连续时间系统的时域分析 ·§2.1系统的数学模型 ● §2.2LT1系统的响应 §2.3LT1系统的冲激响应与阶跃响应 。§2.4卷积 2

2 第二章 LTI连续时间系统的时域分析 • §2.1 系统的数学模型 • §2.2 LTI系统的响应 • §2.3 LTI系统的冲激响应与阶跃响应 • §2.4 卷积

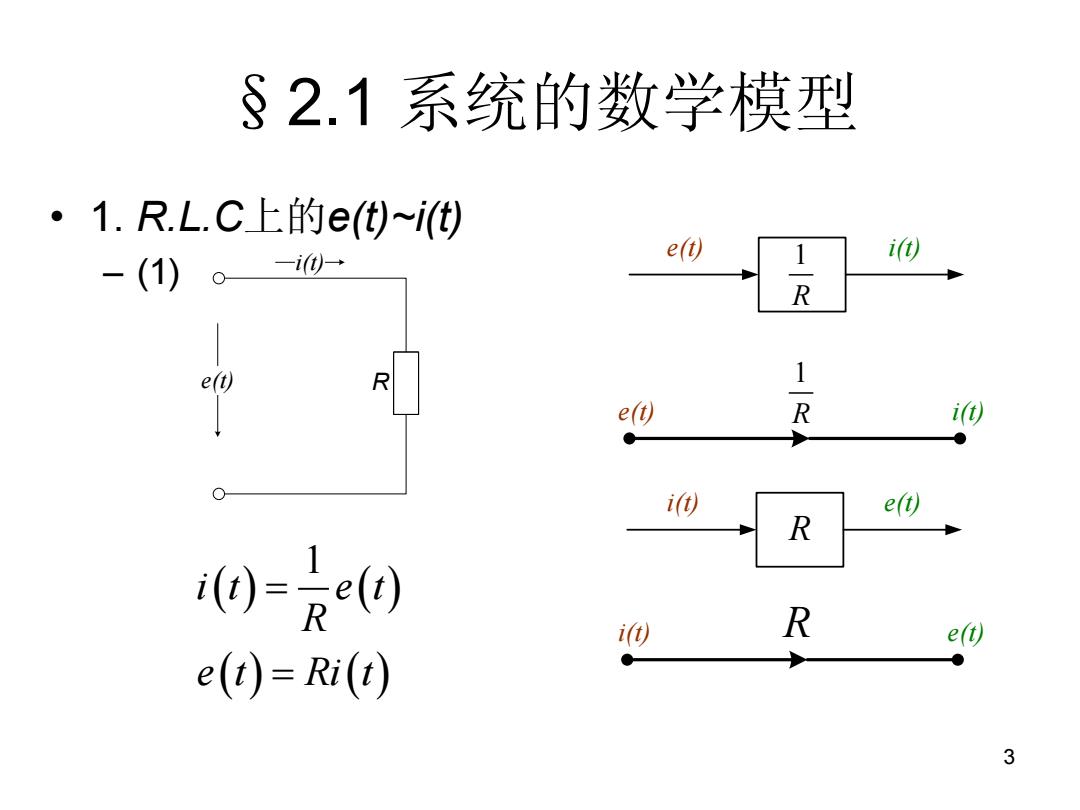
§2.1系统的数学模型 。1.R.L.C上的e()i(t) -(1)。-i0= e() ) R e(t 1 e() R i ● i e(t) R 0-0 i R e() e(t)=Ri(t) 3

3 §2.1 系统的数学模型 • 1. R.L.C上的e(t)~i(t) – (1) R i(t) e(t) e(t) i(t) 1 R 1 e(t) R i(t) i(t) e(t) R i(t) R e(t)         1 i t e t R e t Ri t  

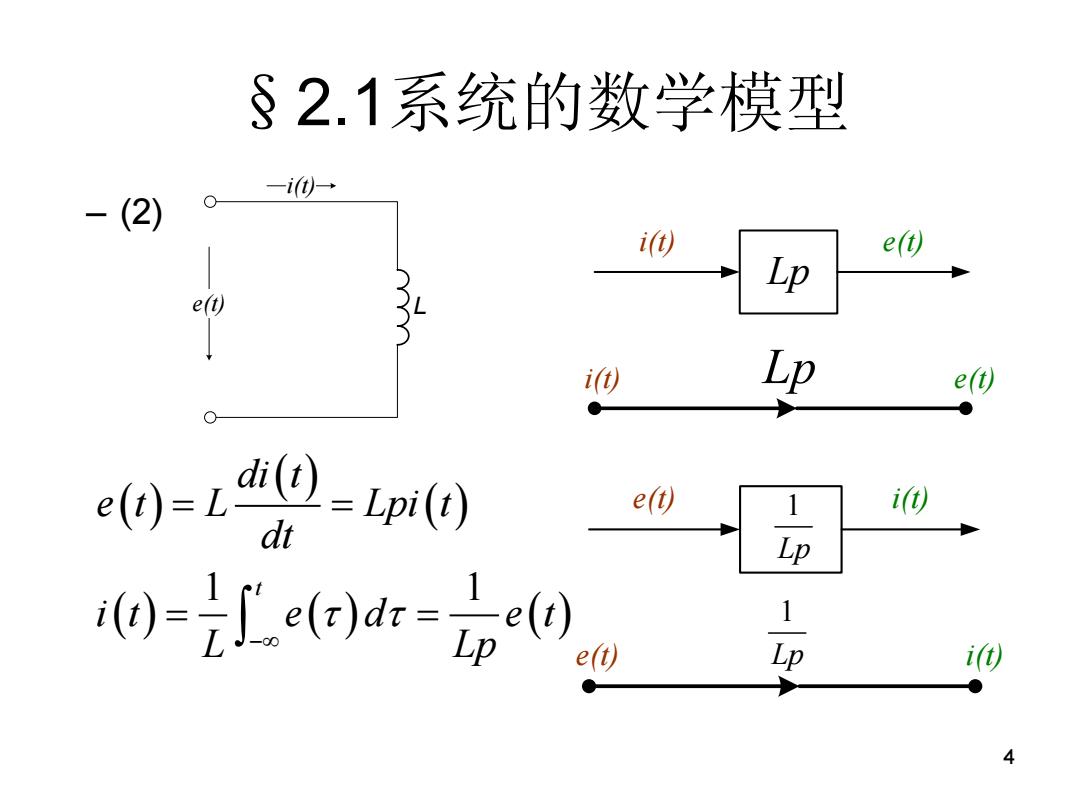
§2.1系统的数学模型 -it)→ (2) i) e(t) p 0 LP e(t) ● 0=9-m e() 1 i1 0=2.ea=e0 1 Lp ) ● 4

4 §2.1系统的数学模型 – (2) i(t) e(t) L             1 1 t di t e t L Lpi t dt i t e d e t L Lp         i(t) e(t) Lp i(t) Lp e(t) e(t) 1 i(t) Lp e(t) i(t) 1 Lp

§2.1系统的数学模型 -i0→ -(3) i() e() Cp 0 CP e() cp() e(t) i() e0-(dr-⑦ e(t) Cp i ● 5

5 §2.1系统的数学模型 – (3) i(t) e(t) C             1 1 t de t i t C Cpe t dt e t i d i t C Cp         e(t) 1 i(t) Cp e(t) i(t) 1 Cp i(t) e(t) Cp i(t) Cp e(t)

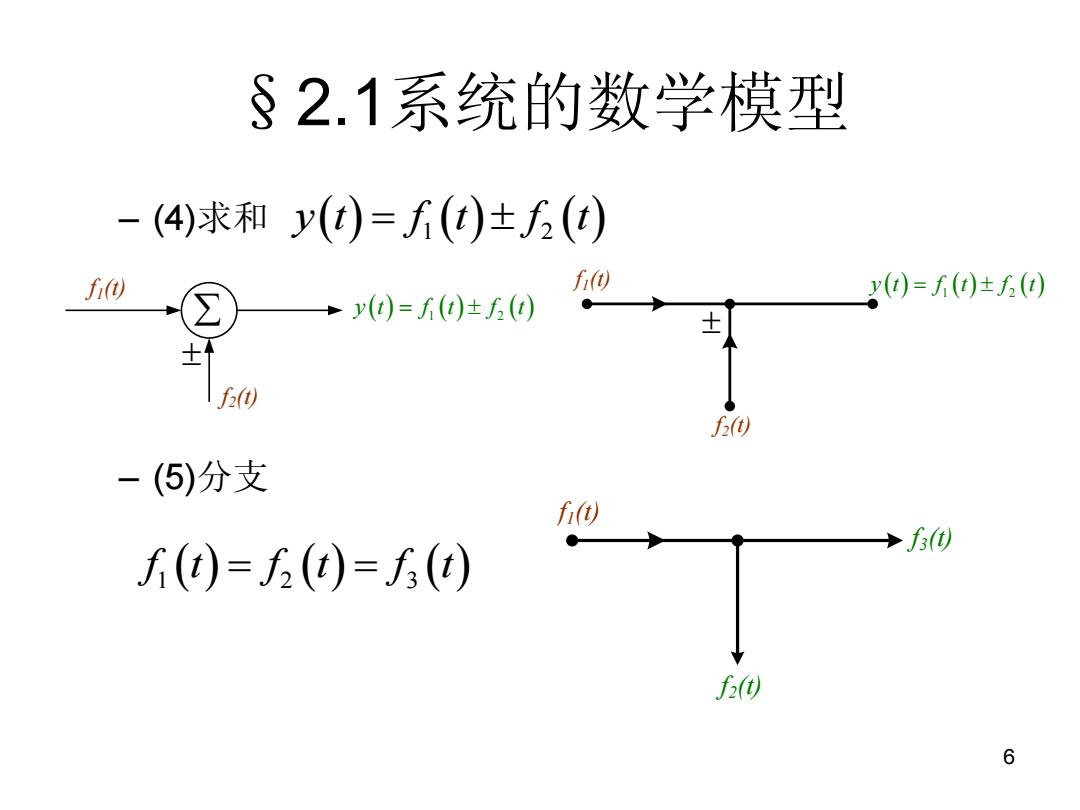
§2.1系统的数学模型 -(4)求和y()=f()±() f +y()=f()±f6() ()=f()±() 士 f( f5) -(5)分支 fi →f) f()=()=5(t) f2) 6

6 §2.1系统的数学模型 – (4)求和 – (5)分支 f1(t)  f2(t)  y t f t f t     1 2     f1(t) f2(t) y t f t f t     1 2      f1(t) f2(t) f3(t) y t f t f t     1 2     f t f t f t 1 2 3        