
10第2章模拟PLL的传递函数 的极点,使阶数超过类型。在一些非常复杂的电路中可以发现十阶乃至十二阶的环 路,但类型仅为1类或2类。 2.2.3环路参数 二阶传递函数(2-15),虽然只有两个极点和一个零点,但却包含了许多系数(增益 和时间常数)。这样写出的传递函数太复杂了;我们可以用一个改进的标记法,使传递 函数表达得比较简洁。一个二阶2类PLL的传递函数可以用两个恰当的环路参数完 全确定。在最初的设计和分析中使用环路参数是非常方便的,在确定出了满足要求的 参数之后,再把这些参数分解为增益和时间常数。本节将对PLL文献中经常出现的两 12组不同的参数给出定义。 1.固有频率和阻尼 二阶PLL中最常用的一组参数是无阻尼固有频率,rd/s(一般称作固有频率)和无量纲 的阻尼系数5。二阶2类PL的这两个参数可以用式(215)中的系数和时间常数定义为 wn= KaKs=KaK.K: (2-16) 5-受√=学-会√ 2 系统传递函数则简化为 H(s9)=子+2Xw3+ 25wns+ar (2-17) 固有频率和阻尼是对于一对极点的环路性质的简便描述,所以非常适合于二阶环路。 如果5<1,这两个极点是一对共轭复根;如果5=1,这两个极点是重合的实根;而当> 1时,这两个极点为不重合的实根。当5<1时,从s平面的原点到极点的矢量长度等 于ω。,而负实轴与该矢量之间的夹角的余弦为5,如图2-3所示。当≥1时,极点位置 的几何平均值即等于,而这两个极点的位置之比为 252+25√52-1-1 0 cos 图2-3复数极点的仙与5的几何表示

2.2二阶PLL11 5的典型值在0.5与2之间,而0.707是最常用的值。有时也使用比这些数大许 多的值,如20或30。阻尼小于0.5的环路的瞬态响应呈现太大的过冲,因此动态性能 13 无法让人满意。远大于1的阻尼因子,只有在一些特殊的情况下才被使用,2.2.4节中 就有这样的一个例子。。有一个非常宽的取值范围,根据需要,其范围大约从105到 l08rad/s,甚至更大。 固有频率和阻尼是受欢迎的一组参数,因为它们有直观的物理解释,还因为它们 大量地出现在PLL的文献中。然而严格地说,这些参数仅适用于二阶环路。的一 个扩展了的定义可适用于高于二阶的2类环路(将在第3章中介绍),但对于一阶PLL 和三类或更高类的PLL而言,这个扩展定义则毫无意义。而且,仙常被用作二阶环路 带宽的衡量。后面我们将指出,用作带宽的衡量并不太合适;我们需要更好的衡量 方式。 2.环路增益K 对于讨论中的二阶2类PLL,我们定义环路增益为 K=KK,K =KaKo (2-18) 这个等式将被看作由比例通路产生的开环增益,但不包含由VCO中的积分而产生的 1/s因子。在2.3.1节中,我们将对K规定一个适用于其他阶数和其他类型PLL的更 广泛的定义。一个二阶环路需要两个参数,只用一个K是不够的。我们可以选用5作 为第二个参数,或者如后文中广泛使用的2也很好。二阶2类PLL的任意两个参数 都可以用任意其他两个参数确定。其中的一些关系为 K=2到n, K .= (2-19)》 Kx2=452, 5=合K 使用K之后,参量化的系统传递函数(2-15)就变为 H(s)= K(s+K/4) K(s+1/x) +K+K74g= 子+Ks+K/2 (2-20) 相应的误差响应为 2 E()=2+K+K/4g 二2+sK+K/x (2-21) 3.DC增益Koc 把PLL的DC增益定义为 Kpc lims G(s)I=KaK.F(0) (2-22) 14 这个定义适用于所有阶数和所有类型的PLL。对于1类环路,F(0)是有界的,而F(s) 中的那些积分器则使2类或2类以上的环路增益变为无穷大。关于K∝的含义将在 5.1.1节中说明
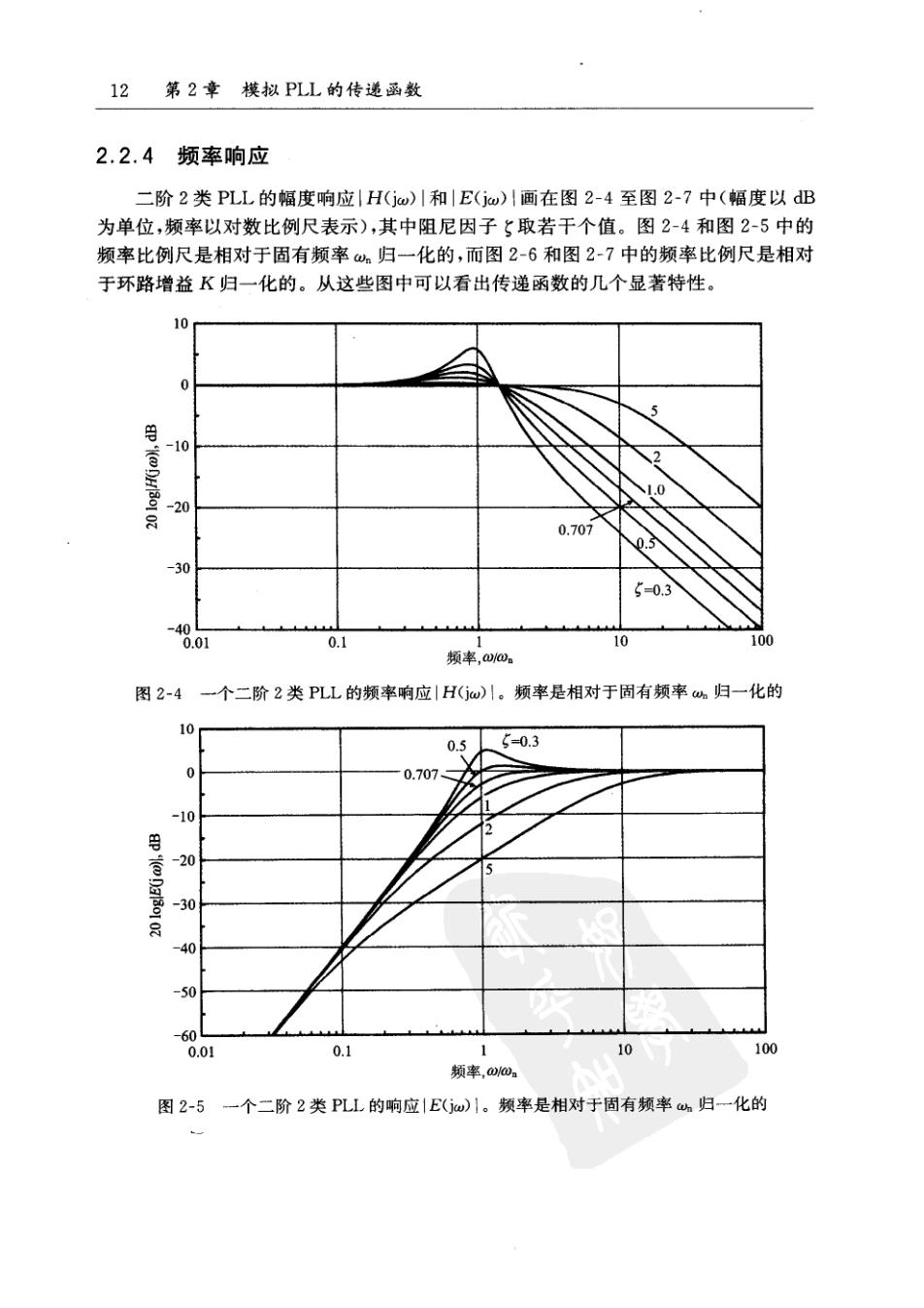
12第2章模拟PLL的传递函数 2.2.4频率响应 二阶2类PLL的幅度响应|H(jw)川和|E(jw)|画在图2-4至图2-7中(幅度以dB 为单位,频率以对数比例尺表示),其中阻尼因子5取若干个值。图2-4和图2-5中的 频率比例尺是相对于固有频率归一化的,而图2-6和图2-7中的频率比例尺是相对 于环路增益K归一化的。从这些图中可以看出传递函数的几个显著特性。 10 0 月 -10 、2 1.0 -20 8 0.707 0. -30 5-0.3 -40 .01 0.1 10 100 频率,aw/ 图2-4一个二阶2类PLL的频率响应|H(jw)川。频率是相对于固有频率,归一化的 10 0.5 5=0.3 0 0.707 -10 -20 1D50102 -30 -50 -60 0.01 0.1 1 10 100 频率,0@a 图2-5一个二阶2类PLL的响应|E(w)1。频率是相对于固有频率h归一化的
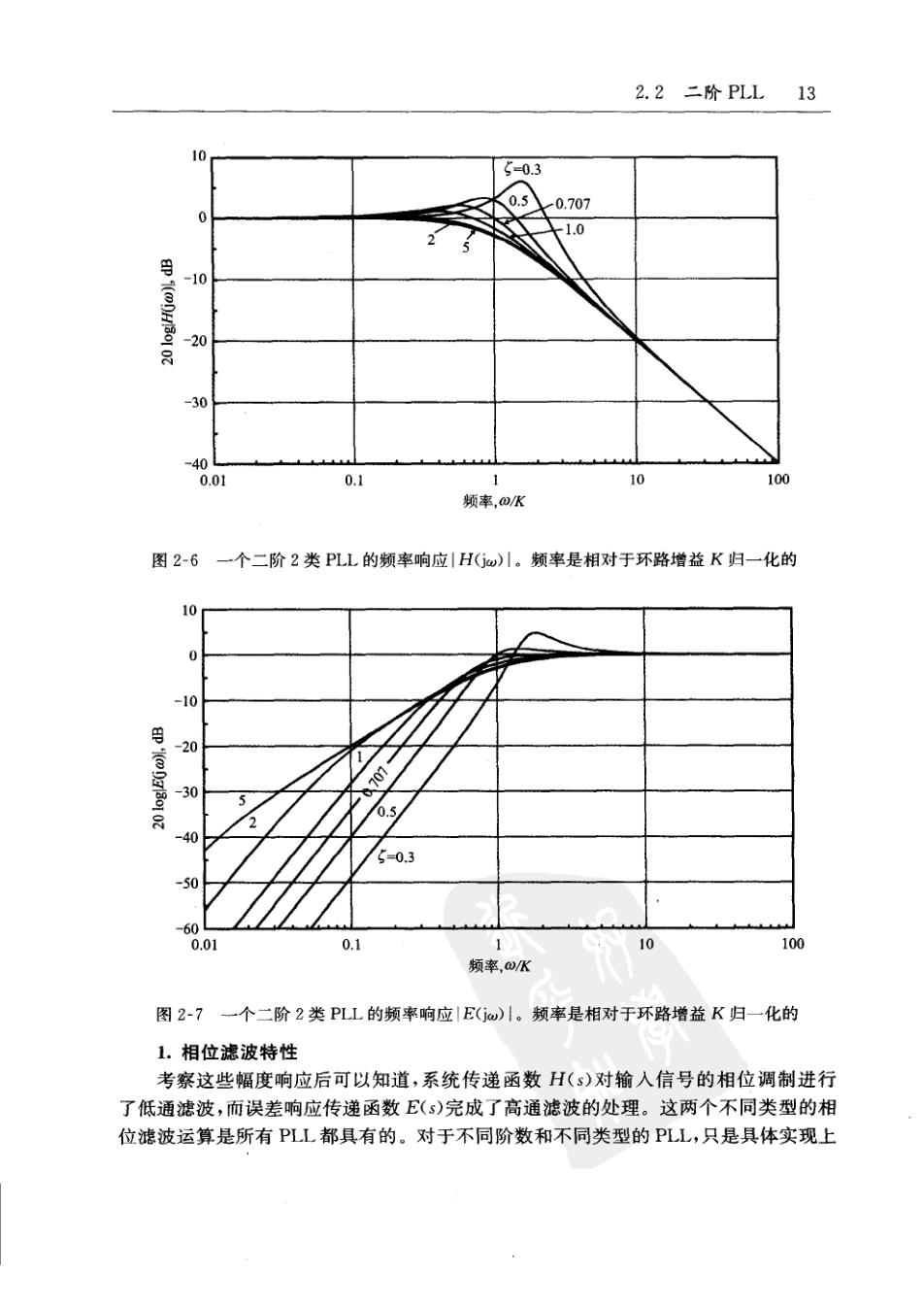
2.2二阶PIL 13 10 5-0.3 0.5 -0.707 0 1.0 2 -10 100H.50-02 -20 -30 -40 0.01 0.1 10 100 频率,①K 图2-6一个二阶2类PLL的频率响应|H(w)川。频率是相对于环路增益K归一化的 10 0 -10 apD13o1 -20 1 -30 707 5 8 0.5 2 -40 5=0.3 -50 -6 0.01 0.1 10 100 频率,ω/K 图2-7一个二阶2类PLL的频率响应E(jw)|。频率是相对于环路增益K归一化的 1.相位滤波特性 考察这些幅度响应后可以知道,系统传递函数H(s)对输入信号的相位调制进行 了低通滤波,而误差响应传递函数E(s)完成了高通滤波的处理。这两个不同类型的相 位滤波运算是所有PLL都具有的。对于不同阶数和不同类型的PLL,只是具体实现上

14第2章模拟PLL的传递函数 的差异。之所以有这样两个滤波特性,是因为PLL的频带必须有限定的范围。对于环 路带宽内的输人信号的相位调制,环路是可以跟踪的,而对于带宽之外的相位调制是 无法跟踪的。因此,在环路带宽内的输入相位调制被传递到VCO的相位输出端,但环 路带宽以外的输人相位调制则被衰减。而误差响应必然是与此互补的:对环路带宽之 内的输入相位调制进行跟踪时误差很小;而对环路带宽之外的输人相位调制,由于无 法跟踪而产生几乎100%的跟踪误差。 15 2.渐近线响应 观察一下频率响应|H(jw)|和|E(jw)1的渐近线是有启发的。从式(2-20)和式 16 (2-21)可以看出,一个二阶2类PLL的渐近线可表示为 〔1,w《K IH(iw)i≈K w 0>K (2-23) u《h E(j){≈ 1, awn 因此,H(jw)|的高频渐近线是以一6dB/倍频的速率下降的,而1E(jw)的低频渐近线 是以十12dB/倍频的速率上升的。这两条渐近线都与阻尼5无关。不同的|H(jw)1渐 近线斜率是由不同阶数的PLL产生,而不同的|E(jw)|的斜率是由不同类型的PLL产 生的。 3.带宽 PLL的带宽应当怎样来定义?实际上并不存在一个能满足所有用途的单一的定 义。可以被选作带宽的参数有:固有频率、环路增益K、噪声带宽B和3B带 宽B。 固有频率是被广泛用于表示带宽的,但只要略看一下图2~4中的低通曲线便可知 17 道,固有频率并不是一个对H(s)满意度的度量值,因为它受到5的强烈影响;我们需要 一个较好的定义。不过,固有频率确实很好地指出了E(s)高通滤波特性的转角频率, 见图2-5。这个对高通滤波频率响应的可用性可以推广到更高阶的2类PLL,但固有 频率这个术语对于任何一个既不是二阶又不是2类的PLL是毫无意义的。 图26表示了K是对于H(s)的低通滤波转角频率的一个很好的表征,而且这种 表征对于任何阶数、任何类型的PLL都同样适用。2.3.1节中将介绍,K的另外一些 特性也非常适合于带宽的定义。在本书的后文中,使用带宽这个术语时就是指使用 K,除非有更恰当的词语。然而,在图2-7中可以看到,K是对于E(s)的高通转角频率 的一个很差的表征。 如果加性白噪声是主要扰动的话,那么6.1.3节中定义的噪声带宽B是一个对 PL带宽的恰当的度量,尽管噪声带宽不太适用于低噪声的情况(这时也许选用K比较 合适)。B与K之间的关系将在第6章中做详细介绍。本书中的B是指噪声带宽。 常用的滤波器一般用3dB带宽来定义。锁相环的带宽似乎也可以这样来定义,但