
第2章 模拟PLL的传递函数 从本质上讲,PLL必然是一种非线性电路,但大多数PLL的主要操作都可以很好 地用线性模型近似。在相位误差很小时,线性模型一般是适用的,这个条件在环路锁 定时都能达到。大多数关于PLL的分析和设计都可以使用这种线性近似的方法:当线 性近似不成立时,PLL的分析就变得异常困难。 在线性分析工具中,拉普拉斯变换和傅里叶变换,以及由此派生出的诸多概念,是 特别有用的。其中的传递函数描述了线性电路在变换域上的输入与输出之间的关系, 是分析PLL的极其有用的工具。PLL的解析设计方法几乎是完全通过传递函数进行 的。应当注意的是,只有线性电路才有传递函数;非线性电路是没有这种性质的。 模拟PLL的传递函数将在本章和下一章介绍,数字PLL的传递函数将在第4章 中介绍。在这几章中得出的结论将应用于本书的其他章节。 2.1基本传递函数 在通常的电路中,传递函数把输人信号和输出信号的电流或电压关联了起来。但 在PLL中,最受关注的输入变量或输出变量是信号的相位,而不是电压或电流。这里 6 考虑的传递函数是把加在PLL中某一点上信号的相位调制与PLL中另一点上的相位 调制响应关联起来。 2.1.1基本单元电路的传递函数 我们来考虑一个由检相器(PD)、环路滤波器(LP)和压控振荡器(VCO)组成的最 基本的锁相环,如图2-1所示。输入信号的相位用A(t)表示,VCO输出的相位用0。(t) 表示,两者都以弧度为单位。我们假设环路是锁定的,而且检相器是线性的,因此PD 的输出电压为 a=Ka(A-a。) (2-1) 其中K。叫做检相器的增益因子,以V/rad(或A/rad)为单位。我们把相位误差定义为 0。=0-d。 (2-2) 误差电压()是被环路滤波器处理的,环路滤波器的作用是建立环路的动态特性。此 外,噪声和信号的高频分量往往被环路滤波器所抑制,但这是次要的功能,这里暂不考 虑。我们用F(s)表示环路滤波器的传递函数。滤波器的输出是一个控制电压,表示为 .(t),用以控制VCO的频率。在拉普拉斯变换域中,环路滤波器的作用可写为
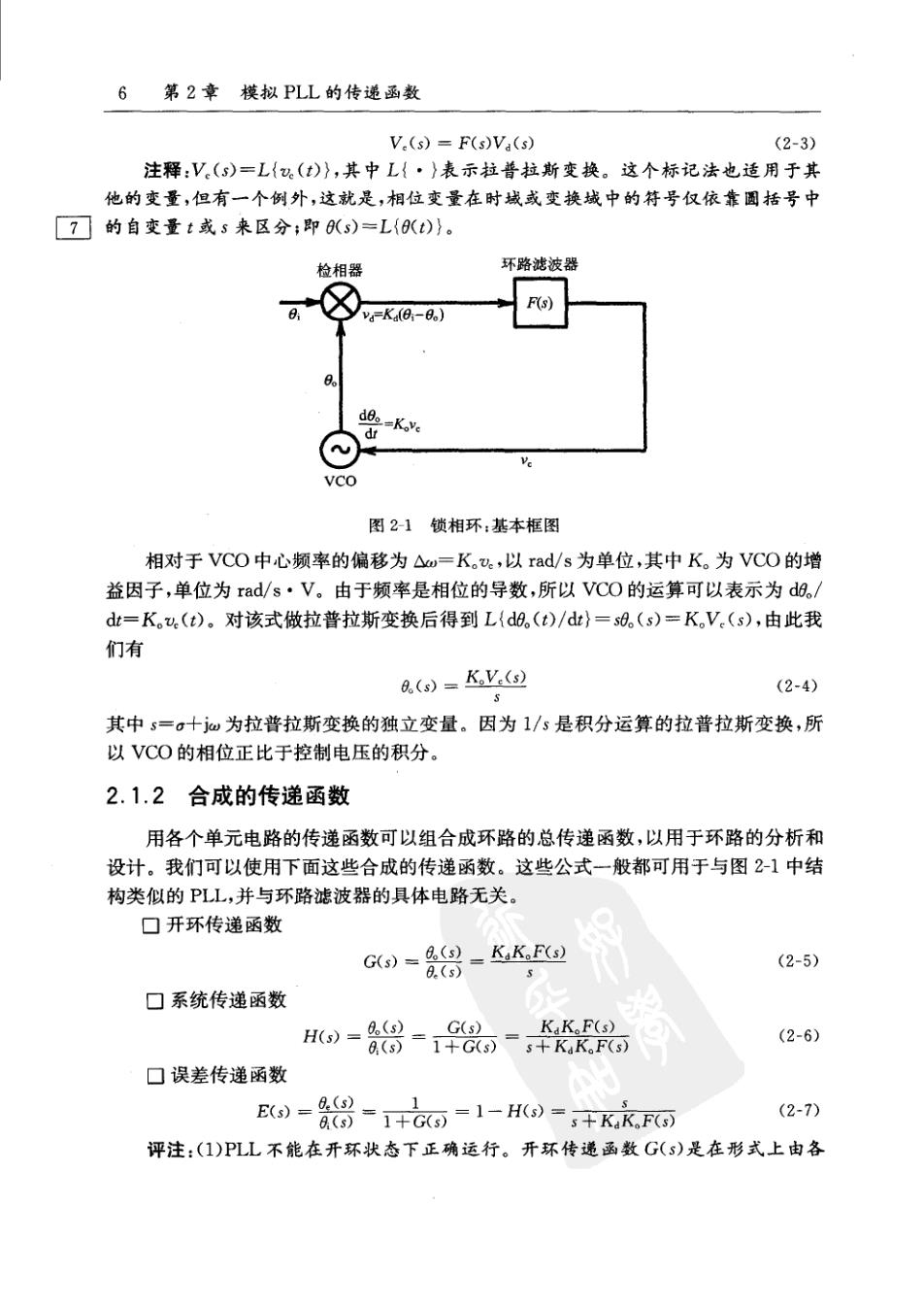
6第2章模拟PLL的传递函数 V(s)=F(s)Va(s) (2-3) 注释:V(s)=L{.(t)},其中L{·}表示拉普拉斯变换。这个标记法也适用于其 他的变量,但有一个例外,这就是,相位变量在时战或变换域中的符号仅依靠圈括号中 的自变量t或s来区分;即(s)=L{(t)}。 检相器 环路滤波器 F(s v=Ka6-d。) deo=K.ve dr Ve 图2-1锁相环:基本框图 相对于VCO中心频率的偏移为△w=K。a.,以rad/s为单位,其中K。为VCO的增 益因子,单位为rad/s·V。由于频率是相位的导数,所以VCO的运算可以表示为d识。/ dt=K。U,(t)。对该式做拉普拉斯变换后得到L{d9。(t)/dt}=s8。(s)=K。V.(s),由此我 们有 0(s)=KV-(s) (2-4) 其中s=。十jw为拉普拉斯变换的独立变量。因为1/s是积分运算的拉普拉斯变换,所 以VCO的相位正比于控制电压的积分。 2.1.2合成的传递函数 用各个单元电路的传递函数可以组合成环路的总传递函数,以用于环路的分析和 设计。我们可以使用下面这些合成的传递函数。这些公式一般都可用于与图2-1中结 构类似的PLL,并与环路滤波器的具体电路无关。 口开环传递函数 G()=(9= KaK.F(s) (2-5) 8.(s) 5 ☐系统传递函数 H(s)=0(s) G(s) KK。F(s) 0(s)1+G(s)s+KaK.F(s) (2-6) 口误差传递函数 E()=A(9 1 A9=1+G=1-H)=+KkF (2-7) 评注:(1)PLL不能在开环状态下正确运行。开环传递函数G(s)是在形式上由各

2.1基本传递函数 7 个单元电路的传递函数级联形成的。这并不是说,反馈回路可以在实际使用中断开, 然后使用简单直接的方法测量出所需的频率响应。不过,这种形式上的开环传递函数 是一个很有用的概念,并将在后文中被反复引用。(2)系统传递函数也一直被叫作闭 环传递函数(比如,在本书的前两版中)。但环路误差也是用闭环传递函数来描述的, 所以“闭环”这个术语的含义就变得模糊不清。我们提议采用系统这个词来避免两 8 义性。 2.1.3特征方程 表达式1十G(s)=0称为PLL的特征方程。特征方程的根(即那些满足方程的s 值)是闭环传递函数的极,点。极点的位置是PLL的重要性质。在大多数PLL中,开环 传递函数可以写成下面的形式 G(s)=A(s) (2-8) B(s) 其中A(s)和B(s)为s的两个代数多项式。把式(2-8)代人式(2-6)和式(2-7)后,得到 H(s)= A(s) B(s) B(S)+A(' E(s)= B(s)+A(s) (2-9) 多项式B(s)十A(s)称为特征多项式,因为该多项式是从特征方程中导出的,并且具有 相同的根。这一多项式将在后文中反复出现。 2.1.4命名法、系数和单位 在上面的方程中,相位是用符号0表示的,并以rd为单位,符号中也会被用到。 频率是用符号w表示的,并以rad/s为单位。但频率也经常用符号f表示,并以Hz为 单位。相应地,有时用“周”(cycle)取代rad来表示相位会比较方便;符号e即是为此而 使用的。在通信界,ε的单元通常称作单位时间间隔(UI)。 除了相位之外,有时使用时间差x会很方便,这里的x以s为单位。0、e、x和信号 频率f。=1/T,这4者之间的关系为 e=于,0=2mf (2-10) 前文介绍过K:和K。这两个量,它们分别是检相器和VCO的增益系数,分别以V/rad 和rad/s·V为单位。类似的一些定义也同样有效。对于检相器,可以使用系数K。,它 由下式定义 a=Kp(e一eo) (2-11) 其中K。的单位是V/cycle。.可以看出,K。=2πK。同样,对于VCO可以使用K.,它定 义为 △f。=Ka (2-12) 9 其中K,的单位是Hz/V。应当看出,K,=K/2x,因此KK。=K。K.。而且应当注意, K:和K。总是以乘积的形式同时出现在传递函数式(2-5)和式(2-7)中的,所以,只要 方便的话,可以用K,K。随意地代替
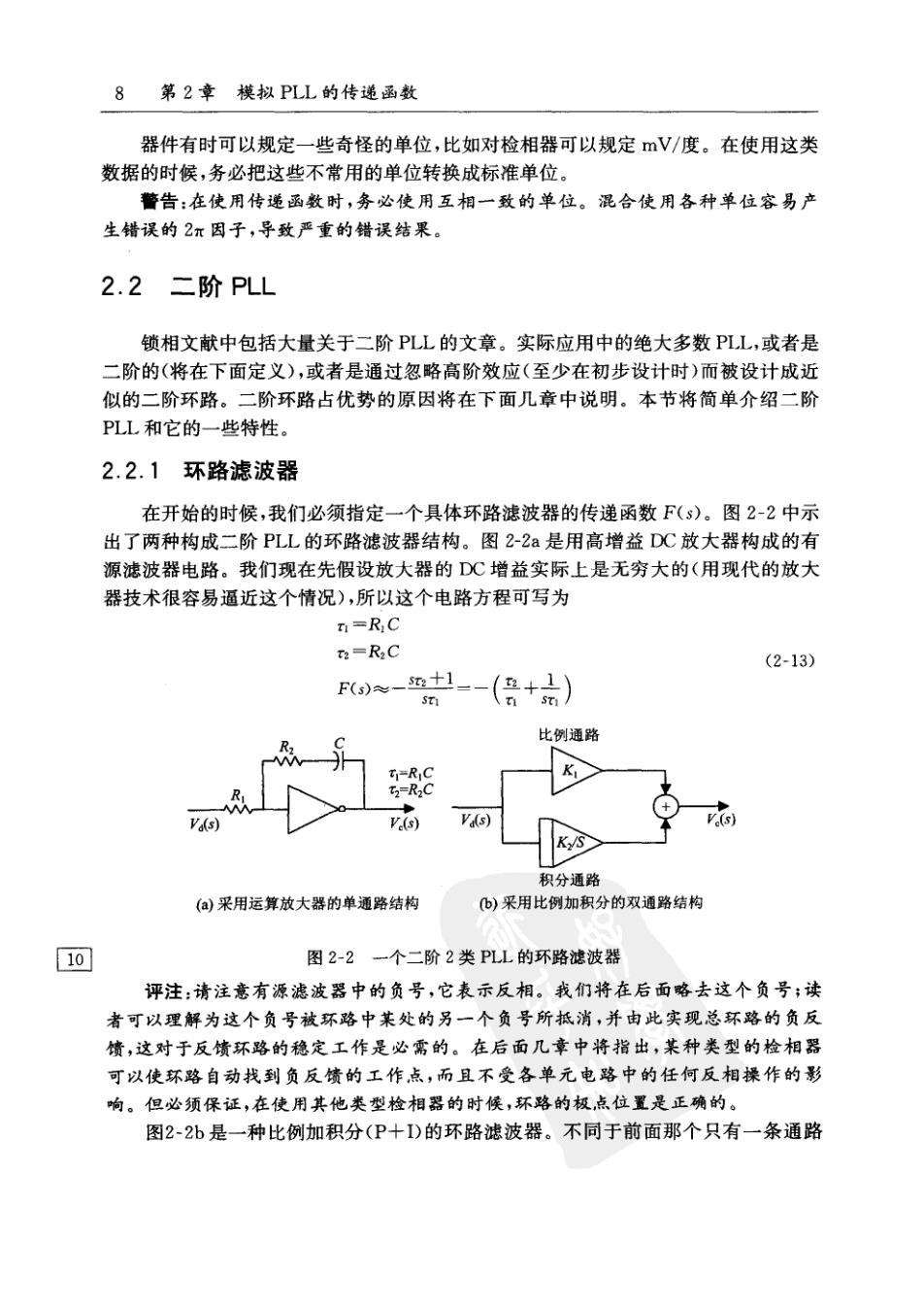
8第2章模拟PLL的传递函数 器件有时可以规定一些奇怪的单位,比如对检相器可以规定V/度。在使用这类 数据的时候,务必把这些不常用的单位转换成标准单位。 警告:在使用传递函数时,务必使用互相一致的单位。混合使用各种单位容易产 生错误的2π因子,导致严重的错误结果。 2.2二阶PLL 锁相文献中包括大量关于二阶PLL的文章。实际应用中的绝大多数PLL,或者是 二阶的(将在下面定义),或者是通过忽略高阶效应(至少在初步设计时)而被设计成近 似的二阶环路。二阶环路占优势的原因将在下面几章中说明。本节将简单介绍二阶 PLL和它的一些特性。 2.2.1环路滤波器 在开始的时候,我们必须指定一个具体环路滤波器的传递函数F(s)。图2-2中示 出了两种构成二阶PLL的环路滤波器结构。图2-2a是用高增益DC放大器构成的有 源滤波器电路。我们现在先假设放大器的DC增益实际上是无穷大的(用现代的放大 器技术很容易逼近这个情况),所以这个电路方程可写为 =RC ta=R2C (2-13) F-中-(g+) 比例通路 T=RIC 2=R2C V.(s) Va(s) V(s) /S 积分通路 (a)采用运算放大器的单通路结构 b)采用比例加积分的双通路结构 10 图2-2一个二阶2类PLL的环路滤波器 评注:请注意有源滤波器中的负号,它表示反相。我们将在后面略去这个负号;读 者可以理解为这个负号被环路中某处的另一个负号所抵消,并由此实现总环路的负反 情,这对于反情环路的稳定工作是必需的。在后面几章中将指出,某种类型的检相器 可以使环路自动找到负反馈的工作点,而且不受各单元电路中的任何反相操作的影 响。但必须保证,在使用其他类型检相器的时候,环路的极,点位置是正确的。 图2-2b是一种比例加积分(P+I)的环路滤波器。不同于前面那个只有一条通路

2.2二阶PLL9 的有源滤波器,这个滤波器有两条通路。滤波器的传递函数方程为 F(s)=K+K (2-14) 其中K1为滤波器的比例通路的增益系数,K2为滤波器的积分通路的增益系数。系数 K,是无量纲的,但K2必须有(时间)-1的量纲,以使总的F(s)为无量纲的。如果K,= x2/x1和K2=1/,那么这两种结构在电学上是等效的。单通路结构在实际中是用得 最多的,但双通路结构在电路实现和分析上有非常多的优点;在后面几章中将给出一 些例子。环路滤波器的其他结构将在后面几页中介绍;上述这两种结构绝不是仅有的 可用的结构。 评注:在事后看来,选用环路滤波器这个名称有所不当,尽管在本书的前两版中传 播过这个术语。我们可以特别地注意一下,这些例子并不是低通滤波器,尽管被有些 作者错误地这样称呼了。一个比较合适的名称可以叫做环路控制器,这是我们控制系 统的同行们使用的术语。这些电路的主要功能是建立反馈环路的动态特性,以及向 VCO提供合适的控制信号。任何对不需要信号的滤除都是次要任务,而且在后面将讲 到,这个滤波任务是由另外的单元电路完成的。但环路滤波器这个词语已经家喻户晓 而难于纠正了,所以本书仍沿用这个术语。 11 2.2.2阶数和类型 现在将式(2-13)和式(2-14)这两个环路滤波器的传递函数代入式(2-6)的基本系 统传递函数中,可以得到 KaK。(sx2+1)/a KaK。(Ks+Kz) H)=F+求Rna+KK/石=子+KKR+KK,K (2-15) 这个传递函数的分母多项式(特征多项式)是二次的,所以这个PLL被叫作二阶的。分 母的两个根是传递函数的两个极点;分子的根是一个零点,位于s=一1/x2=一K2/K1。 零点是P十1滤波器结构所必需的,它对于环路的稳定性是必不可少的。关于这一点, 我们将在2.3.1节中讨论。 在以往的文献中(包括本书的前两版),注意力主要放在环路的阶数上(特征多项 式的次数)。然而,环路的许多重要特性与环路的类型有着更确切的关系,而不是环路 的阶数。类型这个从控制专业中借用过来的术语,是指环路中积分器的个数。因为在 本节中所考虑的这个特定的环路包含了两个积分器(一个在环路滤波器中,另一个在 VCO中),所以除了是一个二阶PLL外,还是一个2类PLL。 因为每一个积分器向传递函数贡献一个极点,所以从这一点来说,阶数永远不会 低于它的类型。但经常会在环路中增加一些非积分器的滤波电路,因而就增加了一些 极点,增加了阶数,但类型不变。由于VCO本质上是执行积分运算的,所以PLL至少 是1类的。2类PLL是被普遍使用的,其理由将在5.1.1节中说明。偶尔也会使用3 类PLL(将在后面讲到很好的理由),而且我曾见过一个4类的PLL。 故意增加滤波电路和电路中存在的不需要的分布元件,可以使环路增加非积分器