
得到(瓦-mg)t=-mV2gh 解得元=mg+m√2gh/t 代入m、h、的值,求得 (1)F=1.92×105N (2)F=1.9×10N 让美子意通回退此
上页 下页 返回 退出 N 得到 ( ) 2 F mg t m gh − = − N 解得 F mg m gh t = + 2 / 代入m、h、t的值,求得 (1) 5 N F = 1.92 10 N 6 N (2) F = 1.9 10 N

解法二考虑从锤自由下落到静止的整个过 程,动量变化为零。 重力作用时间为t+√2h/g 支持力的作用时间为t 根据动量定理,整个过程合外力的冲量为零, 即 Ft-mg(t+√2h/g)=0 得到解法一相同的结果 Fs mg+m2gh/t 江觉子觉返司退欢
上页 下页 返回 退出 解法二 考虑从锤自由下落到静止的整个过 程,动量变化为零。 重力作用时间为 t h g + 2 / 支持力的作用时间为 t 根据动量定理,整个过程合外力的冲量为零, N F t mg t h g − + = ( 2 / ) 0 得到解法一相同的结果 N F mg m gh t = + 2 / 即
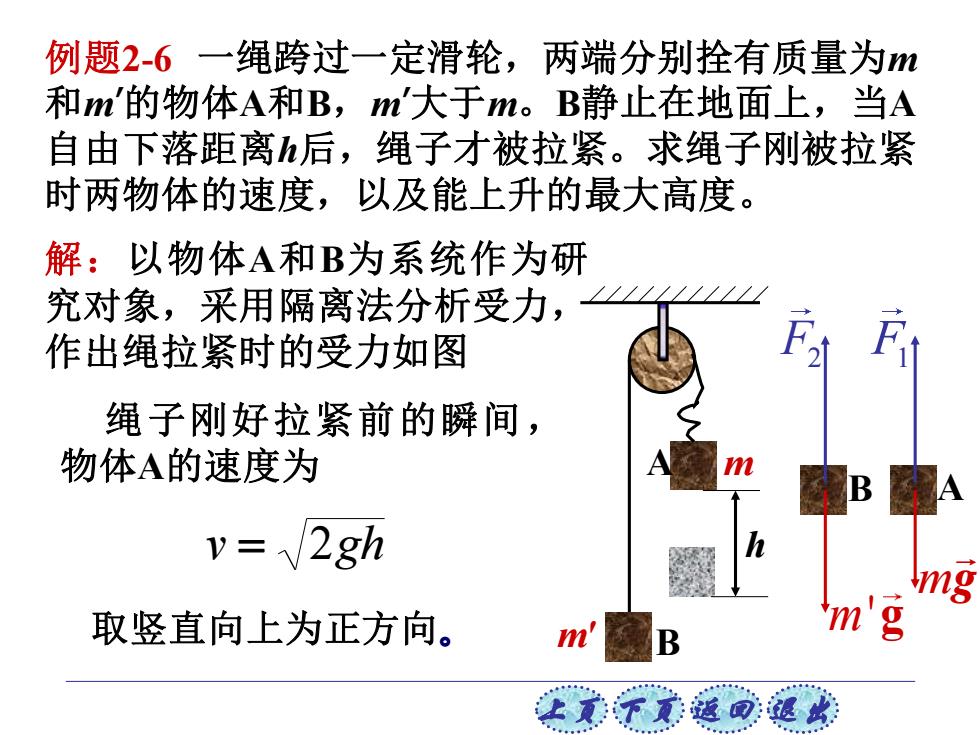
例题2-6一绳跨过一定滑轮,两端分别拴有质量为m 和m'的物体A和B,m'大于m。B静止在地面上,当A 自由下落距离后,绳子才被拉紧。求绳子刚被拉紧 时两物体的速度,以及能上升的最大高度。 解:以物体A和B为系统作为研 究对象,采用隔离法分析受力, 作出绳拉紧时的受力如图 绳子刚好拉紧前的瞬间, 物体A的速度为 y=2gh 取竖直向上为正方向。 m' 'm'g 上下返回退此
上页 下页 返回 退出 例题2-6 一绳跨过一定滑轮,两端分别拴有质量为m 和m ’的物体A和B,m ’大于m。B静止在地面上,当A 自由下落距离h后,绳子才被拉紧。求绳子刚被拉紧 时两物体的速度,以及能上升的最大高度。 m′ m B A h 解:以物体A和B为系统作为研 究对象,采用隔离法分析受力, 作出绳拉紧时的受力如图 A g m F1 B m'g F2 绳子刚好拉紧前的瞬间, 物体A的速度为 v = 2gh 取竖直向上为正方向

绳子拉紧后,经过短暂时间的作用,两物体速率 相等,对两个物体分别应用动量定理,得到 (E-ng)△t=-u-(-mv) (F,-m'g)△t=m'u-0 忽略重力,考虑到绳不可伸长,有 F=E 解得 m√2gh u= m'+m 当物体B上升速度为零时,达到最大高度 2aH=u2-0 m'-m m2h H= a= 8— m'+m m2-m2 王美不美菠回:退收
上页 下页 返回 退出 绳子拉紧后,经过短暂时间的作用,两物体速率 相等,对两个物体分别应用动量定理,得到 1 ( ) ( ) F mg t mu mv − = − − − 2 ( ' ) ' 0 F m g t m u − = − 忽略重力,考虑到绳不可伸长,有 F F 1 2 = 解得 m gh 2 u m m = + 当物体B上升速度为零时,达到最大高度 2 2 0 aH u = − m m a g m m − = + 2 2 2 m h H m m = −
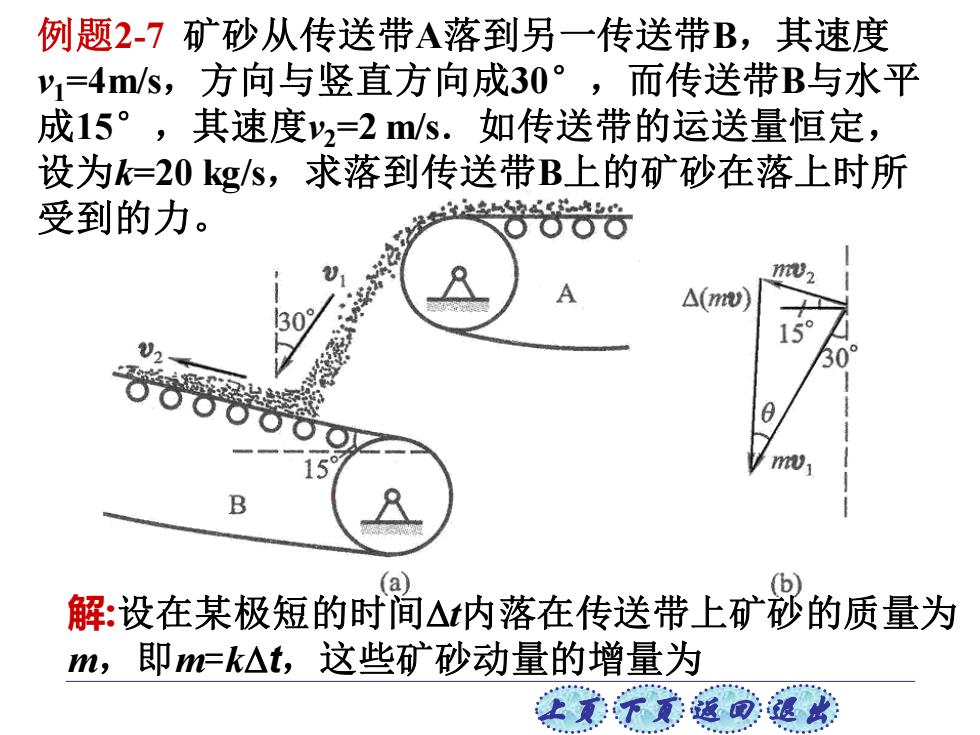
例题2-7矿砂从传送带A落到另一传送带B,其速度 1=4m/s,方向与竖直方向成30°,而传送带B与水平 成15°,其速度y2=2m/s.如传送带的运送量恒定, 设为=20kgs,求落到传送带B上的矿砂在落上时所 受到的力。 102 △(w) 15 309 B a b 解:设在某极短的时间△内落在传送带上矿秘的质量为 m,即m=k公t,这些矿砂动量的增量为 让文子意返回退此
上页 下页 返回 退出 例题2-7 矿砂从传送带A落到另一传送带B,其速度 v1=4m/s,方向与竖直方向成30°,而传送带B与水平 成15°,其速度v2=2 m/s.如传送带的运送量恒定, 设为k=20 kg/s,求落到传送带B上的矿砂在落上时所 受到的力。 解:设在某极短的时间t内落在传送带上矿砂的质量为 m,即m=kt,这些矿砂动量的增量为