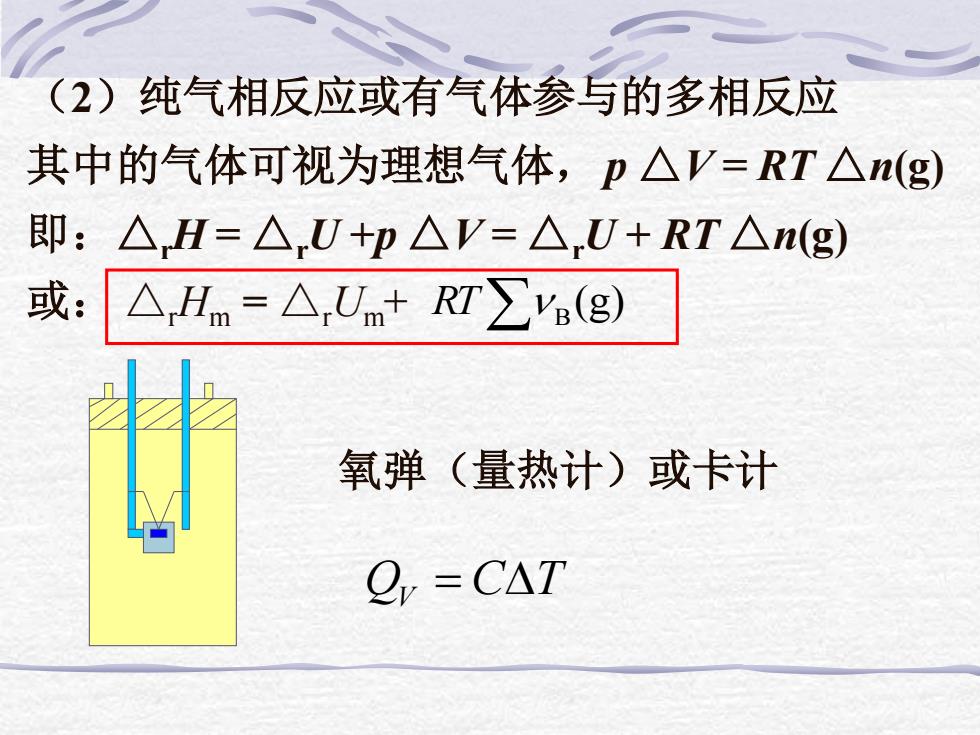
(2)纯气相反应或有气体参与的多相反应 其中的气体可视为理想气体,p△V=RT△n(g) 即:△H=△U+p△V=△U+RT△n(g) 或:△Hm=△,Unm+RT∑(g) 氧弹(量热计)或卡计 =CAT
(2)纯气相反应或有气体参与的多相反应 其中的气体可视为理想气体,p △V = RT △n(g) 即:△rH = △rU +p △V = △rU + RT △n(g) 或: △rHm = △rUm + (g) RT B QV = CT 氧弹(量热计)或卡计
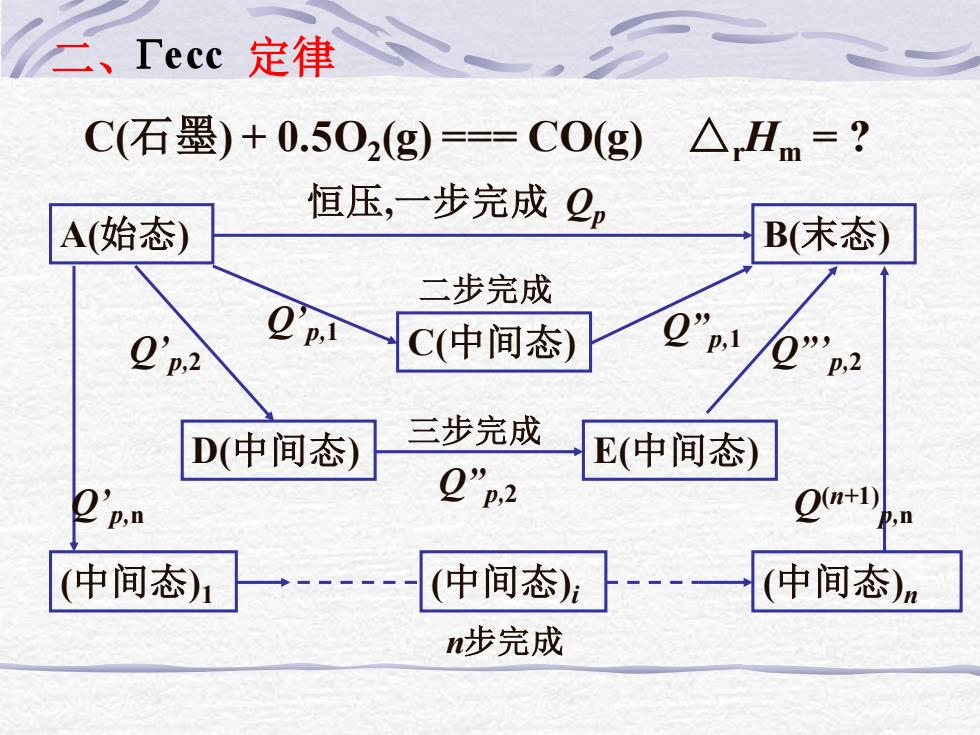
二、Tecc定律 C(石墨)+0.502(g)==C0(g)△Hm=? 恒压,一步完成2p A(始态) B(末态 二步完成 0'p2 C(中间态) Q p,1 p,2 D(中间态) 三步完成 E(中间态) 2"p2 p,n O(n+1) (中间态)1 (中间态) (中间态)n n步完成
A(始态) B(末态) 恒压,一步完成 Qp C(中间态) Q’p,1 Q”p,1 D(中间态) E(中间态) 二步完成 Q’p,2 Q”p,2 Q”’p,2 三步完成 (中间态)1 (中间态)i (中间态)n n步完成 Q’p,n Q(n+1) p,n 二、 定律 C(石墨) + 0.5O2 (g) === CO(g) △rHm = ? ecc

按盖斯定律有: 2p='1+”l =0'p2+2p2+0”"n2 ='pn+2”pn+ P,n 即,热化学方程可以进行代数式一样的加减运算, 故,热效应也可以进行对应的运算。 在无有效功的条件下,△H=2,因此,热效应 的代数和运算就是状态函数的代数和运算
按盖斯定律有: Qp = Q’p,1 + Q”p,1 = Q’p,2 + Q”p,2 + Q”’p,2 = Q’p,n + Q”p,n + + Q(n+1) p,n 即,热化学方程可以进行代数式一样的加减运算, 故,热效应也可以进行对应的运算。 在无有效功的条件下,△rH = Qp,因此,热效应 的代数和运算就是状态函数的代数和运算

C(石墨)+0,(g)==C0,g △,Hmw 可测 -)C0(g)+0.502(g)=C02(g)△Hm2可测 C(石墨)+0.502(g)==C0(g) △Hm=△Hmw-△Hm2 (1)涉及的各反应必须有完整的热化学方程; (2)各反应的条件完全相同; (3)无非体积功存在。 盖斯定律的方法可推广到化学反应的其他状态 函数的计算
C(石墨) + O2 (g) === CO2 (g) △rHm(1) 可测 -) CO (g) + 0.5O2 (g) === CO2 (g) △rHm(2) 可测 C(石墨) + 0.5O2(g) === CO(g) △rHm = △rHm(1) - △rHm(2) (1)涉及的各反应必须有完整的热化学方程; (2)各反应的条件完全相同; (3)无非体积功存在。 盖斯定律的方法可推广到化学反应的其他状态 函数的计算

三、热化学数据的建立及应用 1.标准生成热 ▲定义:在指定条件(p,T)下,由稳定单质 元素反应生成1mol化合物时的热效应。记为: △HO(B,T) 其中B代表所生成的化合物。 特别提醒: ()单质:非单质间的反应不能构成“生成反应”。 C0g)+0.502(g)===C02(g)
特别提醒: (1) 单质:非单质间的反应不能构成“生成反应”。 CO(g) + 0.5O2 (g) ==== CO2 (g) 三、热化学数据的建立及应用 1.标准生成热 ▲定义:在指定条件(p Θ ,T)下,由稳定单质 元素反应生成1mol化合物时的热效应。记为: (B, ) f Hm T 其中B代表所生成的化合物