南京大学：《离散数学》课程教学资源（PPT课件讲稿）Lecture 05 关系与函数

关系的运算(3) 11 逆运算 口R1={(x,)|(,∈R} ■注意：如果R是从A到B的关系，则R1是从B到A的。 ▣(R1)1=R ▣例子：(RUR)1=R11UR21 ■(&，)∈(RUR)1台Uy,x∈(RUR) 台(y,)∈R或，∈R2 台(&，)∈R1或(&，の∈R21

关系的运算(3)  逆运算  R -1 = { (x, y) | (y,x)R} ◼ 注意:如果R是从A到B的关系,则R-1是从B到A的。  (R-1 ) -1 = R  例子：(R1R2 ) -1= R1 -1R2 -1 ◼ (x, y)  (R1R2 ) -1 (y, x)(R1R2 )  (y, x)R1或 (y, x)R2  (x, y)R1 -1或 (x, y)R2 -1 11

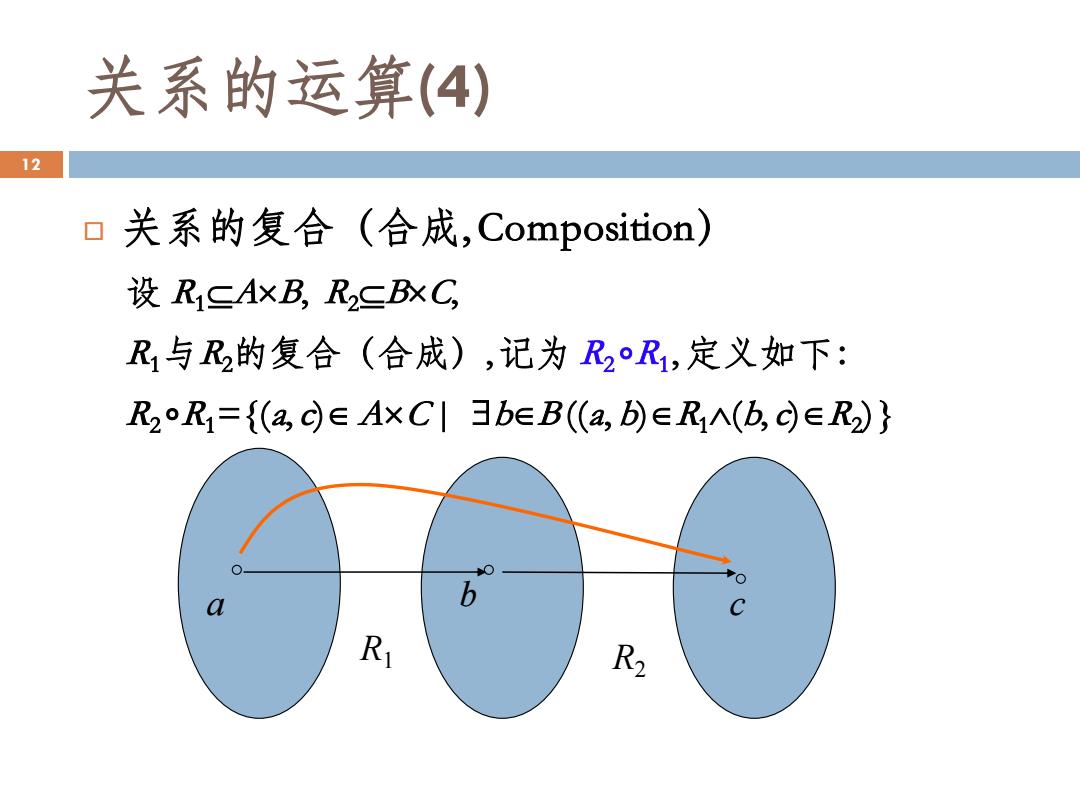
关系的运算(4) 12 口关系的复合（合成，Composition) 设R1SAXB,R2CBxC, R1与R2的复合（合成)，记为R2R1,定义如下： R2R1={(aG∈A×C|3beB(a,b∈RA(b,G∈R2)} b C R R2

关系的运算(4)  关系的复合（合成, Composition） 设 R1AB, R2BC, R1与R2的复合（合成）, 记为 R2 ⃘R1 , 定义如下： R2 ⃘R1={(a, c) AC | bB ((a, b)R1(b, c)R2 )} 12 a b c R1 R2

例：关系的复合运算 13 口设A={ab,c,d},R,R2为A上的关系，其中： R1={(a,a),(a,b),(b,d)} R2={(a,d),(b,c),b,d),(c,b)} 则： R2R1={(a,d),(a,c),(a,d)} R1oR2={(c,d)} R12={(a,a,(a,b),(a,d)}

例：关系的复合运算  设A={a, b, c, d}, R1 , R2为A上的关系，其中： R1 = { (a, a), (a, b), (b, d)} R2 = {(a, d), (b, c), (b, d), (c, b)} 则： R2 ⃘R1= {(a, d), (a, c), (a, d)} R1 ⃘R2 = {(c, d)} R1 2 = {(a, a), (a, b), (a, d)} 13

关系的复合运算的性质 14 口结合律 口给定R1SA×B,R2CBxC,R3CCxD,则： R3°R2)R1=R3°RPR1) 口证明左右两个集合相等 口复合关系的逆关系 口给定R1∈AxB,R2CB×C,则： R2R)1=R16R21 ▣同样，证明左右两个集合相等

关系的复合运算的性质  结合律  给定R1AB, R2BC, R3CD, 则： (R3 ⃘R2 ) ⃘R1 = R3 ⃘(R2 ⃘R1 )  证明左右两个集合相等  复合关系的逆关系  给定R1AB, R2BC, 则： (R2 ⃘R1 ) -1 = R1 -1 ⃘R2 -1  同样，证明左右两个集合相等 14