南京大学：《离散数学》课程教学资源（PPT课件讲稿）Lecture 05 关系与函数

特殊的二元关系 6 口集合A上的空关系：空关系即空集 口全域关系E4:EA={(x)|x,y∈A} 口恒等关系IA:IA={(x)|x∈A} 口函数f:A→B R={(x,()|x∈A}是一个从A到B的一个关系

特殊的二元关系  集合A上的空关系: 空关系即空集  全域关系 EA : EA ={ (x, y) | x, y A }  恒等关系 IA : IA={(x, x) | xA }  函数 f : A→B R={ (x, f(x)) | xA }是一个从A到B的一个关系 6

关系的表示 7 ▣假设A={a,b,Cd,B={&,B,/假设为有限集合 口集合表示：R1={(a,,(b,,(C,,(C)} 0-1矩阵 有向图 a B 0 1 8 a b 1 0 0 10 1 d 00 0 d A B

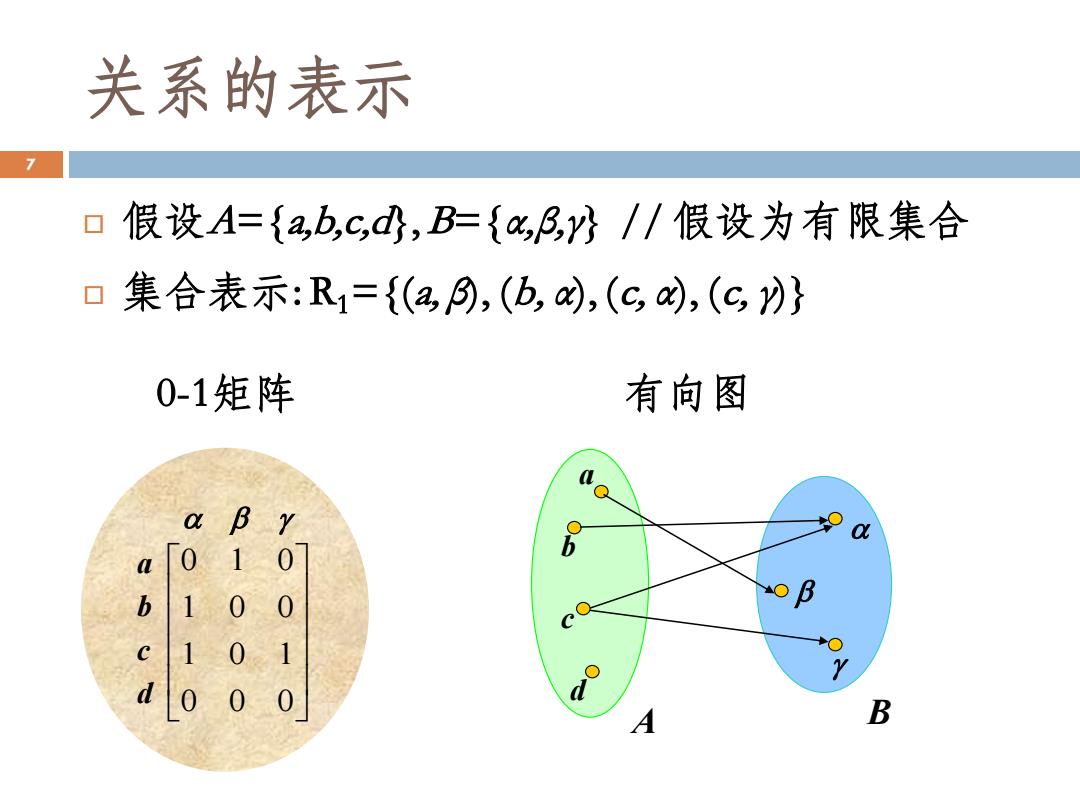
关系的表示  假设A={a,b,c,d}, B={α,β,γ} // 假设为有限集合  集合表示: R1={(a, β), (b, α), (c, α), (c, γ)} 0-1矩阵 有向图 7             0 0 0 1 0 1 1 0 0 a 0 1 0 b c d    a d c b    A B

二元关系和有向图 8 关系RCAxB 有向图(VD,ED) A和B是集合 顶点集VD=AUB 有序对集合 有向边集ED (x,y)ER 从x到y有一条边 若A=B,R中存在序列：(X1,X2), 图D中存在从x到x的长 (X2,X3),,(8n1X) 度为n-1的通路

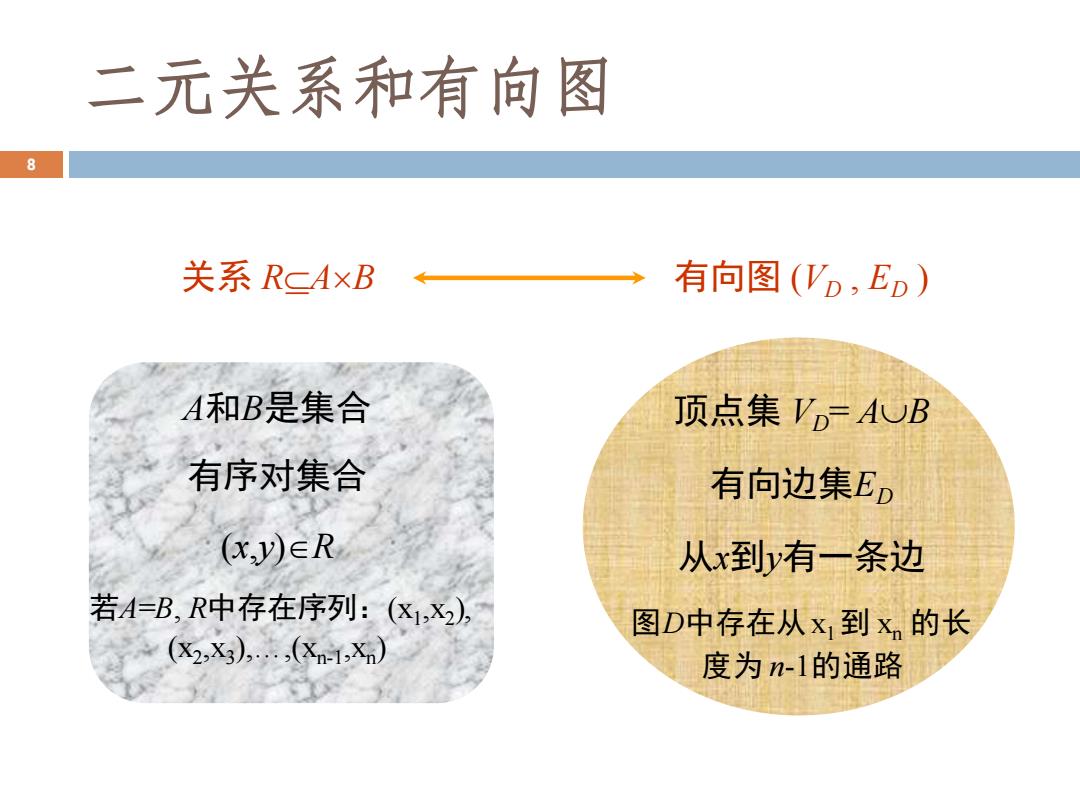
二元关系和有向图 8 关系 RAB A和B是集合 有序对集合 (x,y)R 若A=B, R中存在序列：(x1 ,x2 ), (x2 ,x3 ),…,(xn-1 ,xn ) 有向图 (VD , ED ) 顶点集 VD = AB 有向边集ED 从x到y有一条边 图D中存在从x1 到 xn 的长 度为 n-1的通路

关系的运算(1) 9 口关系是集合，所有的集合运算对关系均适用 口例： ■自然数集合上：“<”U“=”等同于“<” ■自然数集合上：“≤”∩“≥”等同于“=” ■自然数集合上：“<”∩“>”等同于⑦

关系的运算(1)  关系是集合, 所有的集合运算对关系均适用  例: ◼ 自然数集合上: “<”  “=”等同于“” ◼ 自然数集合上: “”  “”等同于“=” ◼ 自然数集合上: “<”  “>”等同于 9

关系的运算(2) 10 口与定义域和值域有关的运算 ▣domR={x|3y(x,)∈R ▣rahR={y|3x(xの∈R) ▣fHdR=dom RUran R 口R个A={(x,の|x∈AΛxR二R restriction也记作RA,R|A 口R[]={y|3x(☒∈AA(xの∈R}=ran(R个)CranR 口例： 口A={1,2,3,4,5},B={1,3,5,6},A上关系R: R={(1,2),(1,4),(2,3),(3,5),(5,2)}, 求RB、RB]

关系的运算(2)  与定义域和值域有关的运算  dom R = {x | y (x,y)R}  ran R = {y | x (x,y)R}  fld R = dom R  ran R  R A = {(x,y) | xA xRy}  R restriction 也记作 𝑅 ↾ 𝐴, 𝑅|𝐴  R[A] = {y | x (xA  (x,y)R)}= ran(RA)  ranR  例：  A={1,2,3,4,5}, B={1,3,5,6}, A上关系R： R={(1,2), (1,4),(2,3),(3,5),(5,2)}, 求 RB、R[B] 10