
太不可逆相变(非正常相变点下的相变) 如:A(I) Ip°△s→A(I) a-cag0r △S A(I) Ip°aS→A(I0 As-cwr 则: As=ClA1,CraAr+a月 T T
★ 不可逆相变(非正常相变点下的相变) A( ) A( ) , , ⎯⎯ ⎯→ 如: T p S A( ) A( ) trs trs , , ⎯⎯⎯ ⎯→ T p S 恒 压 变 温 恒 压 变 温 △S1 △S2 = trs d [A( )] ,m 1 T T p T T nC S = T T p T T nC S trs d [A( )] ,m 2 trs trs ,m ,m trs m d { [A( )] [A( )]} T n H T T n C C S T T p p + − = 则:

例:1mol过冷水在-10℃,p9下结冰,求经该过程 ,体系的熵变△Se 已知水在0℃,p时的凝固热为6.02kJmo; Cpm(冰)-37.6JmoF-K;C.m(水)=75.3 J.moI-1K1. 解:△Hm=△usHm=-6.02 kJ-mol △s=cH,0o0CaH,0sB4r+anA T Trus =-70r+1-g T 273 =-20.59(J.K-) S水>S冰
例:1mol过冷水在-10℃,p Θ下结冰,求经该过程 体系的熵变△S。 已知水在0℃,p Θ时的凝固热为6.02kJ·mol-1; Cp,m(冰)=37.6J·mol-1·K-1 ; Cp,m(水)=75.3J·mol-1·K-1 . 解:△trsHm= △fusHm= - 6.02kJ·mol-1 20.59 (J K ) 273 1 ( 6.02 10 ) d 1 (75.3 37.6) d { [H O(l)] [H O(s)]} 1 3 273 263 fus trs ,m 2 ,m 2 fus m − = − − + − = + − = T T T n H T T n C C S T T p p S水> S冰

过程是否可逆?根据Kirchhoff定律有: 2=△Hi263K=△H(273+打△C,d7 =-6020+(75.3-37.6)×10=-5643(J) 过程的热温商 9、-6 263 =-21.46K)<AS 所以,过程不可逆! 3.隔离体系的熵变 0体=-2环,则△S环=-2体/T环, △S隔=△S体-(2体/T环),上例:△S环=21.46JK-1 故△S隔=-20.59+21.46=0.87JK-1)>0自动
过程是否可逆?根据 Kirchhoff 定律有: Q = △H(263K) = △H(273K) +∫△CpdT = -6020 + (75.3-37.6)×10 = -5643 (J ) 过程的热温商 所以,过程不可逆! S T Q = − = − − 21.46 (J K ) 263 5643 1 3. 隔离体系的熵变 Q体= -Q环,则 △S环= -Q体/T环, △S隔=△S体–(Q体/T环), 上例:△S环 = 21.46J·K-1 故 △S隔=–20.59 + 21.46 = 0.87 (J·K-1 ) > 0 自动
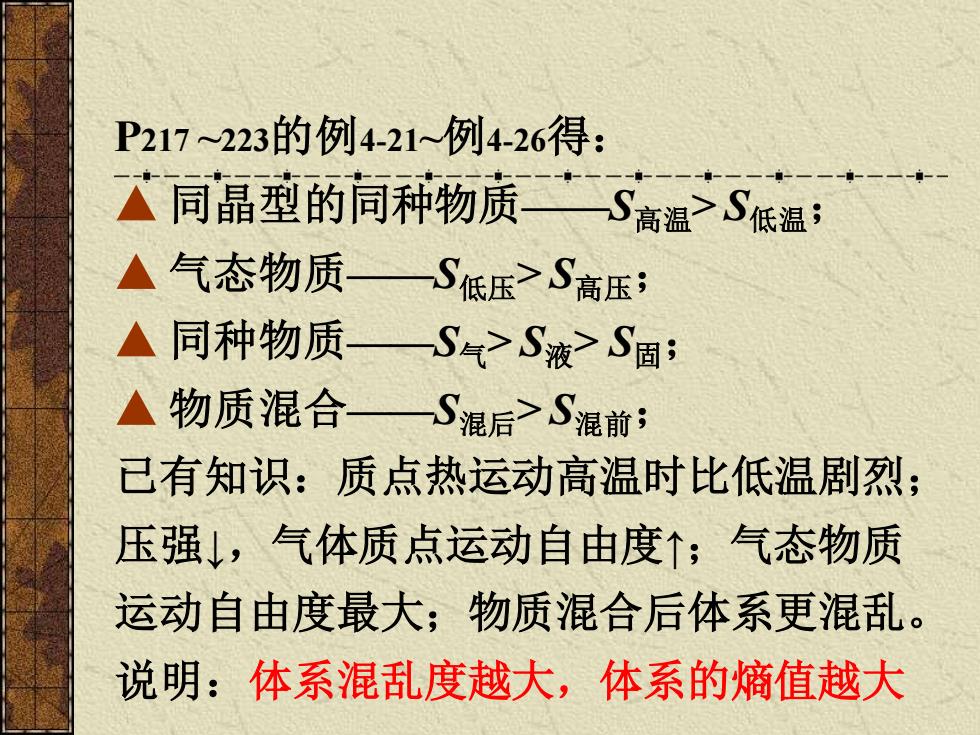
P217~223的例4-21~例4-26得: 广同晶型的同种物质S高温>S低温: ▲气态物质—S低压之S高压: ▲同种物质一S气>S液>S固: ▲物质混合一S混后>S混前: 己有知识:质点热运动高温时比低温剧烈; 压强↓,气体质点运动自由度↑;气态物质 运动自由度最大;物质混合后体系更混乱。 说明:体系混乱度越大,体系的熵值越大
P217 ~223的例4-21~例4-26得: ▲ 同晶型的同种物质——S高温> S低温; ▲ 气态物质——S低压> S高压; ▲ 同种物质——S气> S液> S固; ▲ 物质混合——S混后> S混前; 已有知识:质点热运动高温时比低温剧烈; 压强↓,气体质点运动自由度↑;气态物质 运动自由度最大;物质混合后体系更混乱。 说明:体系混乱度越大,体系的熵值越大

五、熵的统计意义 1.热方学概率(2) a,b,c,d可区分的小球→左右」 根据组合公式:= m! 得: 四个球都在左边C=1,数学概率为1/16 四个球都在右边C=1,数学概率为1/16 三个球在左边,一个球在右边C!=4,数学概率为1/4 三个球在右边,一个球在左边C!-4,数学概率为1/4 二个球在右边,二个球在左边C=6,数学概率为3/8 11<3 16⑧,说明分布越不均匀,概率越小
五、熵的统计意义 1. 热力学概率(Ω) a,b,c,d可区分的小球→ 左 右 ! ( )! ! n m n m C n m − 根据组合公式 = 得: 四个球都在左边 1 ,数学概率为1/16 0 C4 = 四个球都在右边 1 ,数学概率为1/16 0 C4 = 三个球在左边,一个球在右边 4 ,数学概率为1/4 1 C4 = 三个球在右边,一个球在左边 4 ,数学概率为1/4 1 C4 = 二个球在右边,二个球在左边 6 ,数学概率为3/8 2 C4 = 8 3 4 1 16 1 ,说明分布越不均匀,概率越小