2.1带通与低通信号的表示 小结: x(t)=Rex(t)e 低通变为带通 x(t)=x,(t)cos2πft-x(t)sin2πft 的处理过程 一调制 执行这种处理操作的系统 调制器 cos2πfd ,) ) ) x() Re(-) 2r.(0 x(t) 调制器 -sin 2fo! (a) (b) (c) 11
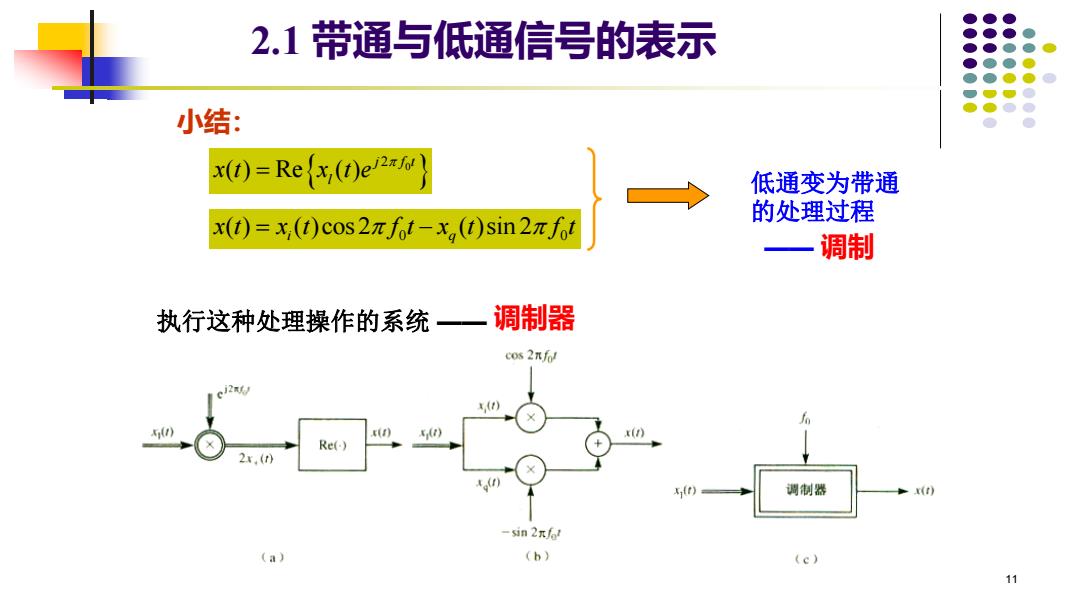
11 小结: 2.1 带通与低通信号的表示 0 0 ( ) ( )cos 2 ( )sin 2 i q x t x t f t x t f t = − 0 2 ( ) Re ( ) j f t l x t x t e = 低通变为带通 的处理过程 —— 调制 执行这种处理操作的系统 —— 调制器
2.1带通与低通信号的表示 x(0)=x,(0)e2=[x)+jR(0e26 =[x(t)cos2πft+(t)sin2πf]+j[(t)cos2πft+x(t)sin2πft] ↓ x,(t)=x(t)cos2πft-x(t)sin2πft x(t)=x,(t)+jx (t) x,(t)=()cos2πft-x(t)sin2πf6d c0s2元/ 2制 从带通信号中 rn) sin 2/ 2x,0 相n2元d 提取低通信号 的处理过程 解调 h 解调器 解调器 0 12
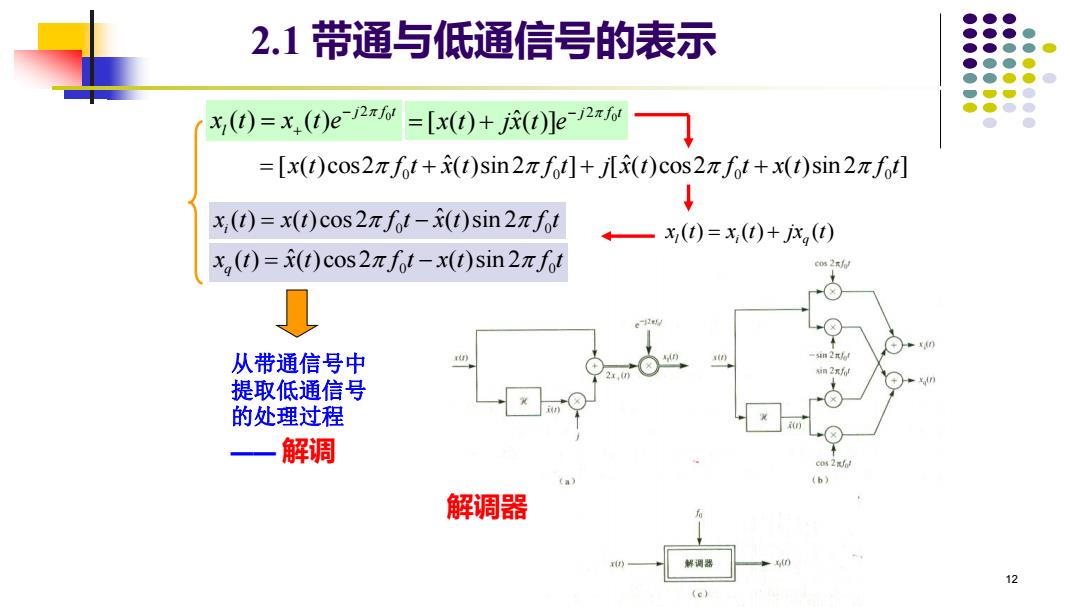
12 2.1 带通与低通信号的表示 0 2 ( ) ( ) j f t l x t x t e− = + 0 2 [ ( ) ( )] ˆ j f t x t jx t e− = + 0 0 ( ) ( ) cos 2 ( ) sin 2 ˆ i x t x t f t x t f t = − 0 0 ( ) ( )cos 2 ( )sin 2 ˆ q x t x t f t x t f t = − 从带通信号中 提取低通信号 的处理过程 —— 解调 解调器 0 0 0 0 = + + + [ ( )cos2 ( )sin 2 ] [ ( )cos2 ( )sin 2 ] x t f t x t f t j x t f t x t f t ˆ ˆ ( ) ( ) ( ) l i q x t x t jx t = +

2.1带通与低通信号的表示 下面导出带通与低通信号频谱和能量之间的关系 顷谱: x()F(Jx(e-dr -(Relx,(Deedr 考虑到实部运算关系: Re5)=5+5) xU=2ix0ew+i0eeakaxU-)+xr-/-0 能量: 考虑到XX0=0, (不重叠) s.-JbiFd-JlxFd-jix.c+x.(F@-2jix.(F 等效低通的能量是带通信号能量的2倍! 13 X,(f)=2X(f+f6)
2 ( ) 1 2 2 2 l l x x f df − = = 13 2 | ( ) ( ) | − + − = + X f X f df 频谱: 2 ( ) [ ( )] ( ) j ft X f F x t x t e dt − − = = ( ) 2 1 Re( ) * = + 2 0 2 Re[ ( ) ] j f t j ft l x t e e dt − − = 0 0 1 2 2 * 2 ( ) [ ( ) ( ) ] 2 j f t j f t j ft X f x t e x t e e dt l l − − − = + * 0 0 1 ( ) ( ) 2 X f f X f f l l = − + − − 考虑到实部运算关系: 2.1 带通与低通信号的表示 2 2 ( ) ( ) x x t dt X f df − − = = 能量: 考虑到 X+ (f)X- (f)=0,(不重叠) 等效低通的能量是带通信号能量的2倍! 2 2 | ( ) | X f df + − = 0 ( ) 2 ( ) X f X f f l = + + 下面导出带通与低通信号频谱和能量之间的关系

2.1带通与低通信号的表示 能量也可以用内积来表示 信号x0,0的内积:<0,0)>=了xe)y(dt=了KYf 显然,信号x(①)的能量: 6=<x(t),x(t)> 带通一低通信号 可以证明:两个具有相同 内积的关系? 的带通信号x(0,y(0的内积: <x0,0>=R©[<x0,y0>] 定义:互相关系数: <x(t),y(t)> Pt.y= 6=28 Pxy=Re(p) 表示两个信号之 间的归一化内积 如果两个信号的内积(或印,)为零,则它们是正交的。 结论: 如果:P=0 那么:Py=0 反之不一定成立。 基带的正交性蕴含着带通的正交性,但反之不亦然! 14
14 2.1 带通与低通信号的表示 * * x t y t x t y t dt X f Y f df ( ), ( ) ( ) ( ) ( ) ( ) − − = = 显然,信号x(t)的能量: 能量也可以用内积来表示 信号x(t), y(t)的内积: = x t x t ( ), ( ) , ( ), ( ) x y x y x t y t = 可以证明:两个具有相同f0 的带通信号x(t), y(t)的内积: , , Re( ) l l x y x y = 结论: 如果: , 0 , 0 x y = l l x y = 那么: 反之不一定成立。 基带的正交性蕴含着带通的正交性,但反之不亦然! 互相关系数: 1 ( ), ( ) Re ( ), ( ) 2 = l l x t y t x t y t 表示两个信号之 间的归一化内积 2 l x = 如果两个信号的内积(或x,y)为零,则它们是正交的。 带通-低通信号 内积的关系? 定义:

2.1带通与低通信号的表示 问题 下面哪个命题是正确的: 1.带通正交,等效低通也一定正交 2.等效低通正交,带通也一定正交 3.等效低通不正交,带通也一定不正交
2.1 带通与低通信号的表示 问题 下面哪个命题是正确的: 1. 带通正交,等效低通也一定正交 2. 等效低通正交,带通也一定正交 3. 等效低通不正交,带通也一定不正交