
2.1带通与低通信号的表示 归纳3个名词的含义及关系 带通信号: x(f) 解析信号: X.(f)=x(Au(f) x,0=0+ x)=[x0+)】 等效低通信号:X,(f)=2X(f+f)
2.1 带通与低通信号的表示 0 ( ) 2 ( ) X f X f f l = + + f0 -f0 | X(f) | 1 ( ) ( ) ( ) ˆ 2 x t x t jx t + = + 归纳 3个名词的含义及关系 带通信号: 解析信号: 等效低通信号: X f ( ) 1 X f X f u f ( ) ( ) ( ) + − = f0 -f0 | X+ (f) | f0 | X (f) | 1 ( ) ( ) ( ) ˆ 2 x t x t jx t + = + -f0

2.1带通与低通信号的表示 X,(f)=2X,(f+f0) 时域: x()=F-[X,(f)] x0=,[x0+)] =2x(t)e-j2xh =三[x(0+u)]e2x =[x(t)cos2πft+x(t)sin2πft]+ +j(t)cos2πjft-x(t)sin2πft] x(t)=Refx,(t)e2 等效低通表达式 任何一个带通信号 都可以用其等效低 xU)=[x,-)+X-f-] 通信号来表示! x以t)一般是复低通信号: x,(t)=x,(t)+jx,(t) 同相分量 正交分量 7
7 0 1 2 ( ) ( ) 2 ( ) − − + = = l l j f t x t F X f x t e 时域: ( ) ( ) ( ) l i q xl ( t )一般是复低通信号: x t x t jx t = + 0 0 0 0 [ ( )cos 2 ( )sin 2 ] ˆ [ ( )cos 2 ( )sin 2 ] ˆ x t f t x t f t j x t f t x t f t = + + + − 2.1 带通与低通信号的表示 0 ( ) 2 ( ) X f X f f l = + + 任何一个带通信号 都可以用其等效低 通信号来表示! * 0 0 1 ( ) ( ) ( ) 2 X f X f f X f f l l = − + − − 0 2 ( ) Re ( ) j f t l x t x t e = 同相分量 正交分量 等效低通表达式 1 ( ) ( ) ( ) ˆ 2 x t x t jx t + = + 0 2 ( ) ( ) ˆ − = + j f t x t jx t e

2.1带通与低通信号的表示 x(t)=x,()+jx,(t) x,(t)=[x(t)cos2πfot+x(t)sin2πf] x,(t)=[(t)cos2πf6t-x(t)sin2πft] 任何一个带通信号都可 x(t)=x,(t)cos2πft-x,(t)sin2πft 以用两个低通信号来表 示!(同相分量,正交 正交表达式 分量) 极坐标形式 由:x,)=x,(0+jx,() x,(t)=r(te8四 其中: r()=Vx()+x0 代入x0=Re{5)e2e,o} 80)=tan,@ x,(t) x(t)=r(t)cos[2zft+e(t)] 极坐标表达式 8
8 ( ) ( ) ( ) l i q 由: x t x t jx t = + 0 0 ( ) [ ( )cos 2 ( )sin 2 ] ˆ q x t x t f t x t f t = − 2.1 带通与低通信号的表示 任何一个带通信号都可 以用两个低通信号来表 示!(同相分量,正交 分量) 极坐标形式 ( ) ( ) ( ) l i q x t x t jx t = + 0 0 ( ) [ ( ) cos 2 ( )sin 2 ] ˆ i x t x t f t x t f t = + 0 0 ( ) ( )cos 2 ( )sin 2 i q x t x t f t x t f t = − ( ) ( ) ( ) x j t l x x t r t e = 1 ( ) ( ) tan ( ) q i x t t x t − = 2 2 ( ) ( ) ( ) x i q r t x t x t = + 0 ( ) ( ) cos[2 ( )] x x x t r t f t t = + 其中: 代入 0 2 ( ) ( ) Re ( ) x j f t t x x t r t e + = 极坐标表达式 正交表达式
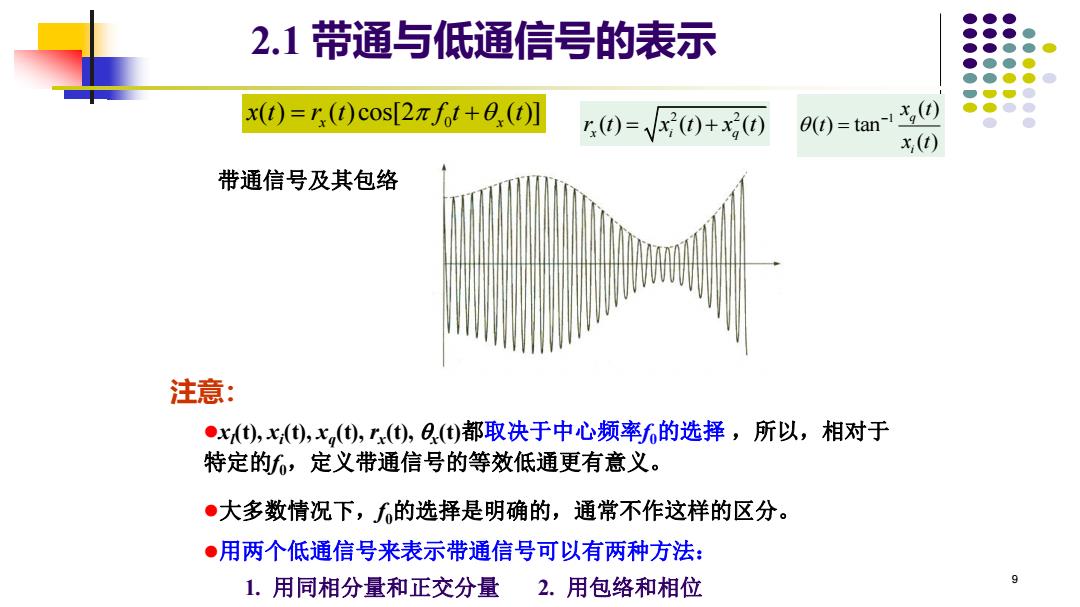
2.1带通与低通信号的表示 x(t)=r,(t)cos[2ft+e(t)] r0=√(0+x回 80=tan1@ x,(t) 带通信号及其包络 注意: ●x),x(),x,(),r(),()都取决于中心频率的选择,所以,相对于 特定的f,定义带通信号的等效低通更有意义。 ●大多数情况下,f的选择是明确的,通常不作这样的区分。 ●用两个低通信号来表示带通信号可以有两种方法: 1.用同相分量和正交分量2.用包络和相位 9
9 1 ( ) ( ) tan ( ) q i x t t x t − = 2 2 ( ) ( ) ( ) x i q 0 r t x t x t = + ( ) ( ) cos[2 ( )] x x x t r t f t t = + 2.1 带通与低通信号的表示 注意: ⚫xl (t), xi (t), xq (t), rx (t), x (t)都取决于中心频率f0的选择 ,所以,相对于 特定的f0,定义带通信号的等效低通更有意义。 ⚫大多数情况下,f0的选择是明确的,通常不作这样的区分。 带通信号及其包络 ⚫用两个低通信号来表示带通信号可以有两种方法: 1. 用同相分量和正交分量 2. 用包络和相位

2.1带通与低通信号的表示 归纳 带通信号的3种表达式(含义,关系,应用) 等效低通表达式: x(t)=Re{x(t)e 分析,计算频谱,功率,带宽. 正交表达式: x(t)=x,(t)cos2nft-x (t)sin2fot 实现,可两路,也可仅一路 极坐标表达式: x(t)=r(t)cos[2zfot+e(t] 直观理解,传输信息承载在高 频信号的包络和相位上
0 ( ) ( ) cos[2 ( )] x x x t r t f t t = + 2.1 带通与低通信号的表示 归纳 带通信号的3种表达式 (含义,关系,应用) 等效低通表达式: 正交表达式: 极坐标表达式: 0 2 ( ) Re ( ) j f t l x t x t e = 0 0 ( ) ( )cos 2 ( )sin 2 i q x t x t f t x t f t = − 分析,计算频谱,功率,带宽… 实现,可两路,也可仅一路 直观理解,传输信息承载在高 频信号的包络和相位上