
6.4应用举例() 966 不连续性结构区 区域1(三维) 连接区 区域3(三维) (区域1:k从1到k1;区域3:k从k2到kf) ■应用普通的三维FDTD分析 ■连接区(交叠区) ●实现三维FDTD分析与一维FDTD分析信 息交换 ●区域边界无法用FDTD方程,缺界外信息 E-V V→E V>E ■连接条件 区域2(一维) ●在k1处应用(6.103)和(6.104),由波导 第1个模 内的电压和电流振幅可算出不连续性区域 端面上的场分布(V→E) 在k1-1处应用(6.105)和(6.106),将不 第n个模 ,+ 连续性区域内的场分布转换为波导端面的 电压和电流振幅(E→V) 7
7 6.4 应用举例(II) 不连续性结构区 (区域 1 : k 从 1 到 k 1; 区域 3 : k 从 k 2 到 k f ) 应用普通的三维FDTD分析 连接区(交叠区) 实现三维FDTD分析与一维FDTD分析信 息交换 区域边界无法用FDTD方程,缺界外信息 连接条件 在k1处应用(6.103 ) 和(6.104 ) ,由波导 内的电压和电流振幅可算出不连续性区域 端面上的场分布( V E ) 在 k 1 - 1 处应用 (6.105) 和(6.106 ),将不 连续性区域内的场分布转换为波导端面的 电压和电流振幅( E V ) 区 域 1 ( 三 维 ) z 1 1 k 2 k f k 连接区 区域3 ( 三 维 ) z yx E V V E V E E V 区域2(一维) 第1个模 第n个模 1 k 1 k 1 2 k 2 k 1
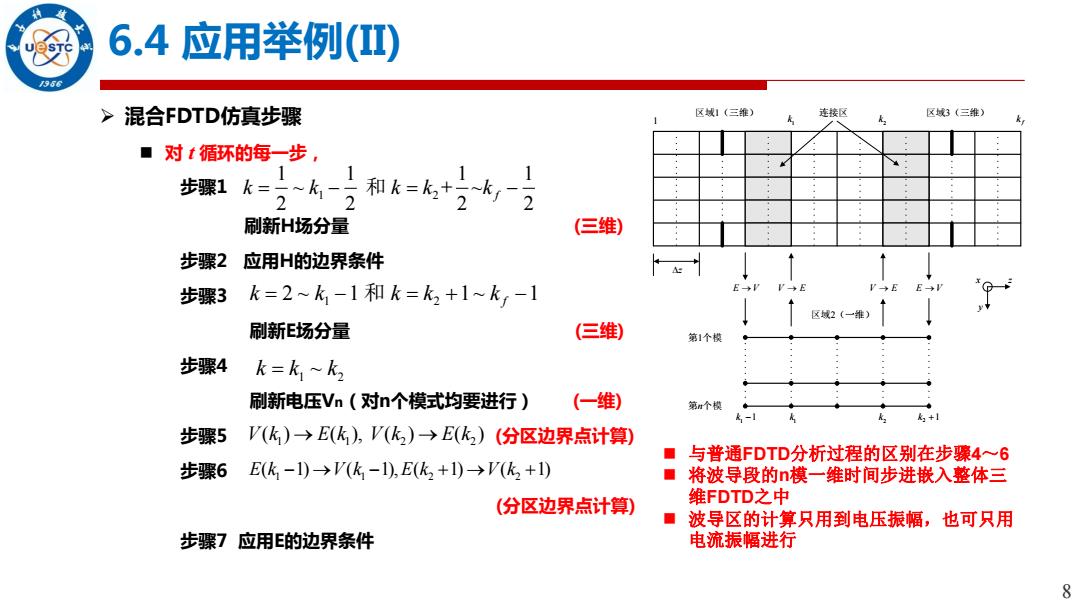
6.4应用举例(I) 966 >混合FDTD仿真步骤 区城1(三推) 连接区 区域3(三维) ■对t循环的每一步, 步骤1k=)~k-2 和k=k+ -k2 刷新H场分量 (三维) 步骤2 应用H的边界条件 步骤3 k=2~k-1和k=k2+1~k,-1 区2(一)↑ 刷新E场分量 (三维) 第1个模 步骤4 k=k~k, 刷新电压Vn(对n个模式均要进行) (一维) 第m个模 k-1 步骤5 V(k)→E(k),V(k2)→E(k)(分区边界点计算) 与普通FDTD分析过程的区别在步骤4~6 步骤6 E(k-1)→V(k-1),E(k+1)→V(k+1) ■ 将波导段的n模一维时间步进嵌入整体三 (分区边界点计算) 维FDTD之中 波导区的计算只用到电压振幅,也可只用 步骤7应用E的边界条件 电流振幅进行 8
8 6.4 应用举例(II) 混合FDTD仿真步骤 对 t 循环的每一步, 步骤1 刷新H场分量 (三维) 步骤2 应用H的边界条件 步骤3 刷新E场分量 (三维) 步骤4 刷新电压Vn(对n个模式均要进行) (一维) 步骤5 (分区边界点计算) 步骤6 (分区边界点计算) 步骤7 应用E的边界条件 与普通FDTD分析过程的区别在步骤4~6 将波导段的n模一维时间步进嵌入整体三 维FDTD之中 波导区的计算只用到电压振幅,也可只用 电流振幅进行 区域1(三维) z 1 1 k 2 k f k 连接区 区域3(三维) z yx E V V E V E E V 区域2(一维) 第1个模 第n个模 1 k 1 k 1 2 k 2 k 1 1 2 1 1 1 1 ~ + ~ 2 2 2 2 f k k k k k 和 1 2 2 ~ 1 1 ~ 1 f k k k k k 和 k k k 1 2 ~ 1 1 2 2 V k E k V k E k ( ) ( ), ( ) ( ) 1 1 2 2 E k V k E k V k ( 1) ( 1), ( 1) ( 1)